4 Light curve analysis

The light curve analysis is quite difficult for the following reasons: (a) no spectroscopic mass-ratio is known; (b) the maxima of the light curve are unequal in brigthness (Max I brighter than Max II); (c) the system undergoes only partial eclipses. An inspection of the light curve reveals that brightness variations occur not only around the maxima, but also at other phases. More specifically, a decrease in brightness is present in the phase interval 0.59-0.87 and a small excess of light is seen around phase 0.32. Other minor light variations can be seen in other phase regions. The magnitude difference between the two maxima is about MaxII - MaxI = 0.03 mag. In modelling light curves of systems exhibiting light curve anomalies, the need to place hot and/or cool spots of solar type has been suggested by several investigators (e.g. Binnendijk 1960; Hilditch 1981; Linnell 1982; Van Hamme & Wilson 1985; Milone et al. 1987; van't Veer & Maceroni 1988, 1989; Maceroni et al. 1990).

  

Table 3: Normal points for YY CMi in light units

4.1 Unspotted solution

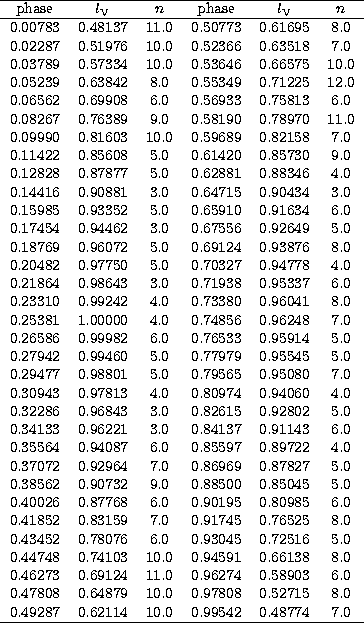
The most recent (1996) version of the Wilson-Devinney (Wilson 1990) synthetic light curve code was used for the light curve solution. 66 normal points, listed in Table 3, were used and weights equal to the number of observations per normal were assigned. Both unspotted and spotted solutions were performed; for the latter, we assumed the presence of cool and hot spots to explain the difference in brightness between the two maxima and the excess of light, respectively. Under these assumptions we excluded the observations in the phase interval 0.59-0.87 from the unspotted solution, since a significant decrease of brightness occurs.

The subscripts 1 and 2 refer to the component eclipsed at primary and secondary minimum, respectively. A preliminary set of input parameters for the DC program was obtained by the Binary Maker 2.0 program (Bradstreet 1993). The DC program was used in the contact mode 3 and in the semidetached mode 4. In the subsequent analysis the following assumptions were made: a mean surface temperature $T_1=6360~\rm K$ according to the spectral type F6V; we assigned typical values for stars with convective envelopes to bolometric albedos and gravity darkening coefficients; limb darkening coefficients were taken from Al-Naimiy's (1978) tables and bolometric linear limb darkening coefficients from Van Hamme (1993). Third light was assumed to be $\ell_3=0$. The adjustable parameters were: the phase of conjunction $\phi_0$, the inclination i, the temperature T₂, the nondimensional potential $\Omega_1$ in mode 3 and $\Omega_2$ in mode 4, the monochromatic luminosity L₁ and the mass-ratio q=m₂/m₁.

Since no spectroscopic mass-ratio of the system is known, a search for the solution was made for a mass-ratio q ranging from 0.2 to 4. The lowest values of the sum $\Sigma(\rm res)^2$ of the weighted squared residuals occured around q=1.0 in mode 3 and q=0.8 in mode 4. Figure 3 shows the fit parameters $\Sigma(\rm res)^2$ as a function of the mass-ratio q in modes 3 and 4. In order to find the final unspotted solution we continued the analysis by applying the DC program for both cases. The two solutions converged to q=0.8921 in mode 3 and q=0.8295 in mode 4. The corresponding values of $\Sigma(\rm res)^2$ were found to be 0.0785 and 0.0835, respectively. Of these two solutions, we finally adopted the solution in mode 3 (with q=0.8921) by taking into account the better fit of the solution in mode 3 and the fact that the secondary exceeds the Roche lobe ($\Omega_2 < \Omega_{\rm in}$) in mode 4. The results of the unspotted solution are given in Table 4 and the corresponding theoretical light curves are shown as dashed lines in Fig. 4.

  

Figure 3: The fit parameter $\Sigma(\rm res)^2$ as a function of the mass-ratio q. Solid lines: mode 3; dashed lines: mode 4

  

Table 4: Light curve solutions of YY CMi

$^{\ast}$assumed.

4.2 Spotted solution

The spotted solution was carried out by adopting the simplest spot model with a physical meaning. We started by assuming that the system had a cool spot on the secondary (cooler) component of the same nature as solar magnetic spots (Mullan 1975). Such a spot could explain the decrease of brightness in the phase interval 0.59 - 0.87. Another hot spot was assumed on the secondary component near the neck region in order to match the light excess around phase 0.32. Such a bright region can be explained as a result of energy transfer from the primary to the secondary component (Van Hamme & Wilson 1985).

The Binary Maker 2.0 program was used to obtain the best fit by adjusting the spot parameters: the latitude b, the longitude l, the angular radius R and the temperature factor $\rm T.F.$ Once the best fit was obtained, the DC program was used to derive the final solution. The program allows the adjustment of spot parameters. The results of the spotted solution are also given in Table 4 and the theoretical light curves are shown as solid lines in Fig. 4. The $\rm O - C$ differences between the observed and calculated points for the unspotted and spotted solution for the system are shown in Fig. 5.

The parameters of the cool spot on the primary component are: latitude $b=90^{\circ}$ (fixed), longitude $l=271.27^{\circ}\pm 0.91^{\circ}$, angular radius $R=22.33^{\circ}\pm 4.51^{\circ}$and temperature factor $\rm T.F.=0.84\pm 0.09$. Those of the hot spot are: latitude $b=90^{\circ}$ (fixed), longitude $l=21.26^{\circ}\pm 1.95^{\circ}$, angular radius $R=9.32^{\circ}\pm 2.69^{\circ}$ and temperature factor $\rm T.F.=1.19\pm 0.09$.A three dimensional picture of the spotted model at phases 0.25 and 0.75 is shown in Fig. 6, while the cross-sectional surface outline of the system together with the respective critical Roche lobes are given in Fig. 7.

  

Figure 4: Normal points and theoretical V light curves of YY CMi. Dashed lines: unspotted solution; solid lines: spotted solution

  

Figure 5: The light curve $\rm (O - C)$ residuals for YY CMi in V band. Crosses refer to unspotted solution; asterisks refer to spotted solution

  

Figure 6: A three-dimensional model of YY CMi for phases 0.25 (upper plot) and 0.75 (lower plot)

  

Figure 7: Cross-sectional surface outline of YY CMi. It coincides with the inner Roche critical surface