5 Radial velocity curves

The primary's radial velocity curve has been measured with the CORAVEL scanner (Baranne et al. 1979) in December-January 1995-1996. The cross-correlation dip is rather wide and shallow due to the fast axial rotation, so that the scatter of the residuals around the fitted curve is rather large (several kms^-1). The secondary component remained invisible to CORAVEL, due to its low luminosity in the blue. About one year later, 14 new observations have been done by E.C. Olson using the Illinois Cassegrain ("white'') spectrograph: 38 cm focal length camera, 831 line mm^-1 grating, Texas Instruments 800$\times$800 CCD detector cooled with liquid nitrogen; the CCD was operated by a Photometric Ltd. controller; spectral resolution in the first order is 0.04 Å per pixel; reductions were done with IRAF.

There has been a problem in fixing the zero-point of the radial velocities obtained with this instrument, so that we fitted an orbit separately to the corresponding data to obtain the apparent systemic velocity. Then we applied to these $V\rm _r$ values a uniform shift equal to the difference between this apparent systemic velocity and that obtained with CORAVEL measurements alone. Indeed, we are confident in the CORAVEL $V\rm _r$ scale, because several standard stars have been observed each night and the small instrumental drifts ($\pm 1$ kms^-1 at most) are well controlled. Therefore, the uncertainties quoted in Table 5 may be slightly optimistic, because they refer to an orbital solution which assumed a perfect correction to Olson's radial velocities.

In order to see the secondary star's spectrum and to obtain the mass ratio of the components, we asked Dr. Didier Raboud to observe TZ Eri in the vicinity of a quadrature with the NTT telescope at ESO. He could indeed take one spectrum, with an exposure time of 10 min, on 11th November 1995, using the EMMI spectrograph in the REMD mode, with Grism #5, Grating #10 and a slit measuring $1''\times 6''$; in this configuration, the resolving power is R=28000 and the wavelengths range between 4013 and 6606 Å. The detector was CCD #36 (ESO numerotation), a thin, back-illuminated Tektronix TK2048EB chip with $24\times 24\,\mu{\rm m}$ pixels. The spectrum has been reduced at Geneva Observatory by Mr. Michel Studer, using the TACOS software developed by Dr. Didier Queloz for the ELODIE spectrograph at Observatoire de Haute-Provence. The radial velocities were obtained by cross-correlation between the observed spectrum and a binary mask optimized for F0-type stars, which yielded two dips, one for each component. Thanks to the long wavelength interval extending well into the red, the cool companion is easily seen in the correlation function. The dips are only 3.6% and 1.1% deep for the primary and secondary respectively, but the S/N ratio of the correlation function is better than 500. A K0-type mask was tried as well and yielded the same result, but with no improvement.

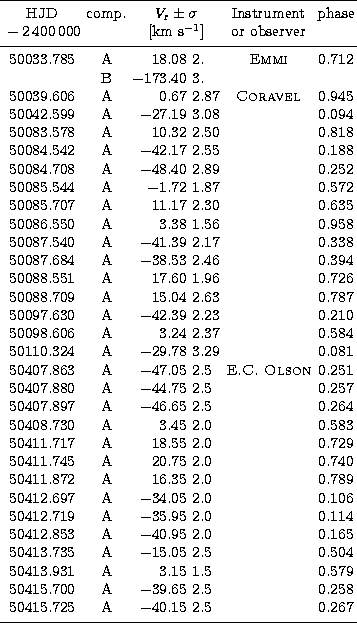
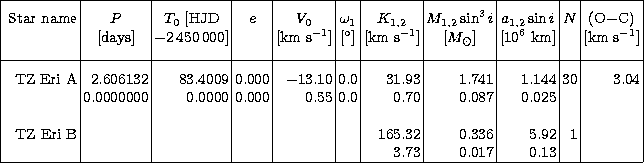
The journal of the radial velocity observations is given in Table 4 and the radial velocity curve is shown in Fig. 3. Additional spectra would of course be welcome to complete the secondary's $V\rm _r$curve, but the single point we have suffices to constrain the mass ratio to a precision of about 7% (q = 0.193 $\pm$ 0.013). The orbital elements are given in Table 5.

   Table 4: Journal of the radial velocity observations of TZ Eri. The phases are computed from the ephemeris given by Eq. (1) and corrected for period change according to Eq. (3)

  

Figure 3: Radial velocity curve of TZ Eridani. The black dots (CORAVEL observations) and the plus signs (Olson's observations) represent the primary component, while the open dot represents the secondary. The phases are those of Table 4

  

Table 5: Orbital elements of the binary. For each component, the second line gives the estimated standard deviations of the parameters. A null uncertainty means that the corresponding parameter has been fixed before the convergence. The period has been fixed to the value it had in the middle of the time spanned by the $V\rm _r$observations

   Table 6: Characteristics of the 7 Geneva passbands (Rufener & Nicolet 1988). $\lambda_{0}$ is the mean wavelength and $\mu$ is the second-order moment (approximately half the passband width)

   Table 7: Adopted values of the logarithmic limb-darkening parameters which were kept fixed in the least-squares solution. For the primary, only the y parameters were fixed (the fitted x parameters are listed in Table 8). For the secondary, both x and y parameters had to be fixed