

Up: Determination of orbital parameters
Subsections
As mentioned in the introduction, very little has been done to find
efficient search methods for the problem of determining orbital parameters in a
general case. An exception is the work by Salo & Laurikainen
(1993) in which an error minimization technique was used to fit
the orbital parameters of NGC 7753/7752. However, in their paper, only three
variables were taken as fitting parameters for the error minimization
technique and other variables, e.g. the masses, were kept fixed.
A common and straightforward method for finding orbital parameters is to carry
out a full search of (part of) the parameter space.
The drawback with such a method is that the number of
simulations needed to achieve acceptable resolution over the parameter space
grows very fast in an N-dimensional space where  . A simple example
should suffice as illustration: In our Run 1, a very close match was obtained
after 100 generations consisting of 500 simulations each, i.e. after 50000
simulations. A full parameter search would only allow
. A simple example
should suffice as illustration: In our Run 1, a very close match was obtained
after 100 generations consisting of 500 simulations each, i.e. after 50000
simulations. A full parameter search would only allow 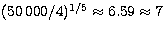 values of each of the parameters
values of each of the parameters 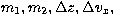 and
and  . The factor 4 in the
denominator comes from the fact that, for each set
. The factor 4 in the
denominator comes from the fact that, for each set 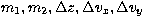 , four values of the spin must be tested. Even
if the spins were assumed to be known, only
, four values of the spin must be tested. Even
if the spins were assumed to be known, only 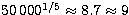 values of each parameter could be tested. With the range
[-50.0,50.0] for
values of each parameter could be tested. With the range
[-50.0,50.0] for  , as used in Run 1, that would give a
resolution of only 100/(9-1) = 12.5 and an equally poor resolution for the
the other parameters. Note also that, for Run 1, the GA found an acceptable
solution already after 20 generations, or 10000 simulations. With 10000
simulations available, a full search would allow only
, as used in Run 1, that would give a
resolution of only 100/(9-1) = 12.5 and an equally poor resolution for the
the other parameters. Note also that, for Run 1, the GA found an acceptable
solution already after 20 generations, or 10000 simulations. With 10000
simulations available, a full search would allow only 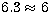 values
of each parameter to be tested, if the spins were known.
values
of each parameter to be tested, if the spins were known.
Clearly, a complete, unbiased search of the whole parameter space is not an
option, at least when the search space is of dimension five or higher. Thus, in order
to carry out a full search, either the number of dimensions must be reduced by fixing
the values of some parameters, or, if all parameters are used, some constraints must
be imposed on the values to be searched. While this is certainly possible in some
cases, the constraints may not always be justified and it may be impossible to find the
correct orbit after imposing the constraints. A strong advantage of the GA method is
that only very loose constraints need to be imposed, even when the
number of parameters is large.
Even though mutations (which play a subordinate role) are random, selection is not,
and a GA is strongly different from a random search.
In order to illustrate the non-randomness of the GA method,
a calculation was carried out in which the values of the parameters
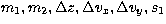 , and s2 were generated
at random. A total of 10000 random sets of parameters were generated,
corresponding to 20 generations of 500 simulations each for the GA. In Fig.
5, the results of the first 20 generations of Run 1 are
compared with the results of the random run. The GA took the lead already
after 6 generations, and the difference in performance should be obvious
from the figure.
, and s2 were generated
at random. A total of 10000 random sets of parameters were generated,
corresponding to 20 generations of 500 simulations each for the GA. In Fig.
5, the results of the first 20 generations of Run 1 are
compared with the results of the random run. The GA took the lead already
after 6 generations, and the difference in performance should be obvious
from the figure.
 |
Figure 5:
Comparison of the performance of a GA and a random search. The dashed
line corresponds to the random search. The vertical axis shows fitness values and the
horizontal axis the number of individuals evaluated |
Whereas the artificial data sets used so far were noise-free, real data sets
are invariably noisy. Furthermore, even if the noise levels are low, in real data there
will always be other deviations from the idealized situation used in the GA simulations.
For example, the mass-to-light ratio need not be constant.
Table 5:
Results from the two runs with noisy input data. The upper row shows
the orbital parameters of the best simulation in generation 100 for the run with
10% noise added, the middle row shows the same parameters for the run with
30% noise added, and the bottom row shows the orbital parameters corresponding to
the observational data. Note that an exact match is impossible in this case, because
of the noise added to the data
|
|
Therefore, in order to be useful, the GA method must be able to function even in
the presence of noise.
I have tested the noise sensitivity by first adding  noise to the
data set used in Run 1.
The noise was added by changing the values of the masses in the grid of
observational data according to
noise to the
data set used in Run 1.
The noise was added by changing the values of the masses in the grid of
observational data according to
|  |
(6) |
where mi,j denotes the mass in cell (i,j), and 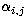 are random
numbers between
are random
numbers between  and
and  , where
, where  is the
noise level. Thus, for the run with
is the
noise level. Thus, for the run with  noise,
noise,  was equal to 0.1.
The results are shown in the upper row of Table 5, from which
it is evident that 10% noise does not stop the GA from finding the correct solution.
The results from a run with
was equal to 0.1.
The results are shown in the upper row of Table 5, from which
it is evident that 10% noise does not stop the GA from finding the correct solution.
The results from a run with 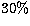 noise are shown in the middle row of
Table 5. Even in this case, the GA manages to find a solution fairly close
to the correct one.
noise are shown in the middle row of
Table 5. Even in this case, the GA manages to find a solution fairly close
to the correct one.


Up: Determination of orbital parameters
Copyright The European Southern Observatory (ESO)
![]() . A simple example
should suffice as illustration: In our Run 1, a very close match was obtained
after 100 generations consisting of 500 simulations each, i.e. after 50000
simulations. A full parameter search would only allow
. A simple example
should suffice as illustration: In our Run 1, a very close match was obtained
after 100 generations consisting of 500 simulations each, i.e. after 50000
simulations. A full parameter search would only allow ![]() values of each of the parameters
values of each of the parameters ![]() and
and ![]() . The factor 4 in the
denominator comes from the fact that, for each set
. The factor 4 in the
denominator comes from the fact that, for each set ![]() , four values of the spin must be tested. Even
if the spins were assumed to be known, only
, four values of the spin must be tested. Even
if the spins were assumed to be known, only ![]() values of each parameter could be tested. With the range
[-50.0,50.0] for
values of each parameter could be tested. With the range
[-50.0,50.0] for ![]() , as used in Run 1, that would give a
resolution of only 100/(9-1) = 12.5 and an equally poor resolution for the
the other parameters. Note also that, for Run 1, the GA found an acceptable
solution already after 20 generations, or 10000 simulations. With 10000
simulations available, a full search would allow only
, as used in Run 1, that would give a
resolution of only 100/(9-1) = 12.5 and an equally poor resolution for the
the other parameters. Note also that, for Run 1, the GA found an acceptable
solution already after 20 generations, or 10000 simulations. With 10000
simulations available, a full search would allow only ![]() values
of each parameter to be tested, if the spins were known.
values
of each parameter to be tested, if the spins were known.
