

Up: The gain-elevation correction of
Subsections
The experimental determination of  ,
, 0), and
0), and

 (
( ), is preferentially made at short wavelengths
despite the higher atmospheric noise and less precise atmospheric correction,
in particular at low elevations. Figure 1 shows the gain-elevation dependence
at 1.22 mm wavelength obtained from on-off measurements (30''
wobbler throw) with the MPIfR bolometer of the quasar 0923+392 and the
extended source Mars (14'' diameter). The bolometer has a taper of
), is preferentially made at short wavelengths
despite the higher atmospheric noise and less precise atmospheric correction,
in particular at low elevations. Figure 1 shows the gain-elevation dependence
at 1.22 mm wavelength obtained from on-off measurements (30''
wobbler throw) with the MPIfR bolometer of the quasar 0923+392 and the
extended source Mars (14'' diameter). The bolometer has a taper of
 -10 dB, a bandwidth of
-10 dB, a bandwidth of 
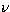
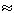 60 GHz, and for
observations of the planets an effective wavelength
60 GHz, and for
observations of the planets an effective wavelength 

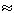 1.22 mm (245 GHz), as calculated from the spectral energy distribution
of the planets and the wavelength dependent atmospheric attenuation. Figure 1
shows also the gain-elevation dependence calculated from Eq. (2) and Eq. (3)
for the best-fit values
1.22 mm (245 GHz), as calculated from the spectral energy distribution
of the planets and the wavelength dependent atmospheric attenuation. Figure 1
shows also the gain-elevation dependence calculated from Eq. (2) and Eq. (3)
for the best-fit values  (0) = 0.085 mm and
(0) = 0.085 mm and  (90) = 0.075 mm
derived from the lsq-fit of the 245 GHz bolometer measurements, using R =
0.9. The figure shows furthermore the gain-elevation dependence derived from
the FE calculations. Comparison of these curves shows that the rms-values
(90) = 0.075 mm
derived from the lsq-fit of the 245 GHz bolometer measurements, using R =
0.9. The figure shows furthermore the gain-elevation dependence derived from
the FE calculations. Comparison of these curves shows that the rms-values

 (
( ) predicted from the FE calculations are
) predicted from the FE calculations are  10
- 15% lower than those derived from the radiometric measurements.
10
- 15% lower than those derived from the radiometric measurements.
Inserted in Fig. 1 is the gain-elevation dependence for 3 mm (100 GHz), 2
mm (150 GHz), and 0.86 mm (350 GHz) wavelength, derived from scaling of the
empirical 1.22 mm gain-elevation dependence by using the best-fit values
 (0) and
(0) and  (90) in Eq. (2) and Eq. (3).
(90) in Eq. (2) and Eq. (3).
![\begin{figure}
\includegraphics [height=6cm]{1530f1.eps}\end{figure}](/articles/aas/full/1998/18/ds1530/Timg27.gif) |
Figure 1:
Gain-elevation dependence measured with the MPIfR bolometer at
1.22 mm (245 GHz) on the quasar 0932+392 [open circles] and Mars (14'')
[dots] (Feb. 1995). The heavy line shows the best-fit gain-elevation
dependence Eq. (3) derived from these measurements; the dashed line shows the
corresponding gain-elevation dependence derived for the surface deformations
predicted from the finite element calculations. The other lines show the
gain-elevation dependence at 3 mm (100 GHz): a), 2 mm (150 GHz):
b), and 0.86 mm (350 GHz): c), derived from scaling of the 1.22
mm gain-elevation dependence (heavy line) |
 |
Figure 2:
Beam pattern
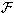 ( ( 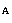 , , 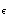 , , ) of the IRAM
30-m telescope calculated for ) of the IRAM
30-m telescope calculated for  = 1.30 mm (230 GHz) and the elevation
angle 0 = 1.30 mm (230 GHz) and the elevation
angle 0 a), 22.5 a), 22.5 b), 43 b), 43 c), 67.5 c), 67.5 d), and
90 d), and
90 e). The reflector is optimized at e). The reflector is optimized at  0 = 43 0 = 43 so
that at this elevation the calculated reference beam is the perfect beam
pattern. Heavy contours: levels at -3 dB, -6 dB, and -9 dB; thin contours:
levels at -12 dB, -15 dB, -18 dB, and -21 dB so
that at this elevation the calculated reference beam is the perfect beam
pattern. Heavy contours: levels at -3 dB, -6 dB, and -9 dB; thin contours:
levels at -12 dB, -15 dB, -18 dB, and -21 dB |
In a diffraction calculation we derived the illumination weighted beam patterns
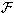 (
(
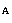 ,
,
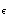 ,
, )
(
)
(
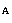 = azimuth direction,
= azimuth direction, 
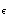 = elevation
direction) degraded by the wavefront deformation of the homology deformations
= elevation
direction) degraded by the wavefront deformation of the homology deformations

 (
( ) predicted from the FE calculations
) predicted from the FE calculations![[*]](/icons/foot_motif.gif) , which
were scaled in amplitude by
, which
were scaled in amplitude by  10 - 15
10 - 15 to match the empirical values
to match the empirical values

 (
( ). As example, Fig. 2 shows for several elevation
angles the calculated beam pattern at
). As example, Fig. 2 shows for several elevation
angles the calculated beam pattern at  = 1.30 mm (230 GHz), i.e. at
the wavelength of the 12CO(2-1) line. From these and similar beam
patterns we calculated for disk-like and constant surface brightness sources
of diameter
= 1.30 mm (230 GHz), i.e. at
the wavelength of the 12CO(2-1) line. From these and similar beam
patterns we calculated for disk-like and constant surface brightness sources
of diameter 
 [
[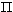 (
(
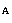 ,
,
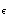 ) = 1 for
) = 1 for

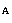 2 +
2 + 
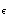 2
2  (
(
 /2)2 and
/2)2 and 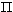 (u,v) = 0 for (
(u,v) = 0 for (
 /2)2
<
/2)2
< 
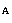 2 +
2 + 
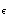 2] the
received power
2] the
received power
| 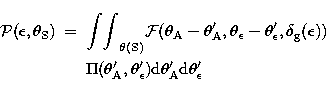 |
|
| (5) |
and the corresponding gain-elevation dependence
| 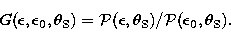 |
(6) |
Table 2 summarizes the on-axis gain-elevation dependence
 ,
,
 = 0)
= 0)  G0(
G0( ) derived from
the diffraction calculations, and to be applied on the IRAM 30-m telescope
for observations at
) derived from
the diffraction calculations, and to be applied on the IRAM 30-m telescope
for observations at  = 3 mm (100 GHz), 2 mm (150 GHz), 1.30 mm (230
GHz), and
= 3 mm (100 GHz), 2 mm (150 GHz), 1.30 mm (230
GHz), and  = 0.86 mm (350 GHz). For an estimated
error of
= 0.86 mm (350 GHz). For an estimated
error of 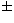 10
10 in the values
in the values 
 (
( ), the accuracy
of the values G0 is
), the accuracy
of the values G0 is 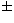 2
2 at long wavelengths (3 mm -
2 mm) and
at long wavelengths (3 mm -
2 mm) and 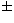 5
5 at short wavelengths (1.3 mm - 0.8 mm). As
evident from Fig. 1 and Table 2, the gain-elevation dependence at 3 mm
wavelength is only a few percent and usually below the accuracy of the
measurements. The small difference between the curves of Fig. 1 and the
data of Table 2 is due to the empirical determination and the calculation of
at short wavelengths (1.3 mm - 0.8 mm). As
evident from Fig. 1 and Table 2, the gain-elevation dependence at 3 mm
wavelength is only a few percent and usually below the accuracy of the
measurements. The small difference between the curves of Fig. 1 and the
data of Table 2 is due to the empirical determination and the calculation of
 ,
, 0); however, the difference is below the accuracy
of the measurements.
0); however, the difference is below the accuracy
of the measurements.
Table 2:
On-axis gain-elevation dependence
G0( ,
, 0) for
0) for  = 3 mm (100 GHz), 2 mm
(150 GHz), 1.3 mm (230 GHz), and 0.86 mm (350 GHz) [receivers of
= 3 mm (100 GHz), 2 mm
(150 GHz), 1.3 mm (230 GHz), and 0.86 mm (350 GHz) [receivers of  -13
dB edge taper]. The accuracy of
-13
dB edge taper]. The accuracy of 
 and R
and R
 is
is

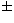 10
10
|
|
An extended source is covered by a larger fraction of the beam than a
point-source and hence should show a smaller gain-elevation dependence. To
quantify this effect, we use the loss in gain
| 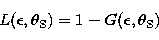 |
(7) |
and display in Fig. 3 the relative loss in gain
 (
( ,
,
 ) between a point-source (
) between a point-source (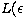 ,0))
and an extended source (
,0))
and an extended source (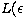 ,
,
 )) calculated from
)) calculated from
| 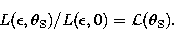 |
(8) |
The calculations show as important result that the quantity
 (
(
 ) is nearly independent of the wavelength and the
elevation of the observation
) is nearly independent of the wavelength and the
elevation of the observation![[*]](/icons/foot_motif.gif) . Using the data of Fig. 3 and the entries of Table 2,
the actual value
. Using the data of Fig. 3 and the entries of Table 2,
the actual value  ,
, 0,
0,
 ) for an extended
source is
) for an extended
source is
| 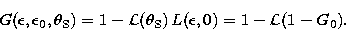 |
(9) |
Figure 3 shows that 0.95 
 (
(
 ) for sources not exceeding
) for sources not exceeding


 2
2
 so that from Eq. (9) for these sources
so that from Eq. (9) for these sources
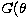
 )
) 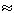 G0, within 5 - 10
G0, within 5 - 10 . The
gain-elevation dependence is weaker for more extended sources since for these
. The
gain-elevation dependence is weaker for more extended sources since for these
 (
(
 ) < 0.9. The gain-elevation dependence is negligible
for sources of diameter 8
) < 0.9. The gain-elevation dependence is negligible
for sources of diameter 8



 since for
these
since for
these  (
(
 )
)  0.1 and
0.1 and 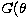
 )
) 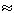 1.
1.
We explain in the following example how to correct observations with the 30-m
telescope. Suppose a source of 
 = 30'' diameter, observed at
1.3 mm wavelength and 20
= 30'' diameter, observed at
1.3 mm wavelength and 20 elevation, has a flux corrected for atmospheric
attenuation of S'(
elevation, has a flux corrected for atmospheric
attenuation of S'(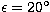 ) =
(2 k/A)
) =
(2 k/A)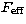
 /
/
 = 10 Jy. The diameter
of the source is 30''/
= 10 Jy. The diameter
of the source is 30''/

 3 beamwidth. From Fig. 3
we find
3 beamwidth. From Fig. 3
we find  (3) = 0.70, so that from Eq. (9) and the value
G0(20
(3) = 0.70, so that from Eq. (9) and the value
G0(20 ) = 0.92 of Table 2 we have G(30'') =
1 - 0.70(1 - 0.92) = 0.94. The homology-corrected telescope-independent
flux is S = S'(20
) = 0.92 of Table 2 we have G(30'') =
1 - 0.70(1 - 0.92) = 0.94. The homology-corrected telescope-independent
flux is S = S'(20 )/ 0.94 = 10.6 Jy. A 10 Jy point-source observed
under similar conditions has the intrinsic flux S = 10/0.92 = 10.9 Jy.
)/ 0.94 = 10.6 Jy. A 10 Jy point-source observed
under similar conditions has the intrinsic flux S = 10/0.92 = 10.9 Jy.
![\begin{figure}
\includegraphics [height=6cm]{1530f3.eps}\end{figure}](/articles/aas/full/1998/18/ds1530/Timg49.gif) |
Figure 3:
Relative gain-elevation dependence
 ( ( S) (Eq. (8)) as function of source size S) (Eq. (8)) as function of source size
 S (in units of beamwidth S (in units of beamwidth  b), for b), for  = 2.0
mm (150 GHz): triangles, = 2.0
mm (150 GHz): triangles,  = 1.30 mm (230 GHz): squares, = 1.30 mm (230 GHz): squares,  =
0.86 mm (350 GHz): circles. The dashed vertical line indicates the diameter
of the full beam =
0.86 mm (350 GHz): circles. The dashed vertical line indicates the diameter
of the full beam  2.4 2.4 b, i.e. the position of the
first minimum b, i.e. the position of the
first minimum |


Up: The gain-elevation correction of
Copyright The European Southern Observatory (ESO)
![]() (0) and
(0) and ![]() (90) in Eq. (2) and Eq. (3).
(90) in Eq. (2) and Eq. (3).
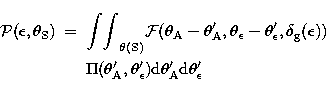
![]()
![]() = 30'' diameter, observed at
1.3 mm wavelength and 20
= 30'' diameter, observed at
1.3 mm wavelength and 20![]() elevation, has a flux corrected for atmospheric
attenuation of S'(
elevation, has a flux corrected for atmospheric
attenuation of S'(![]() ) =
(2 k/A)
) =
(2 k/A)![]()
![]() /
/![]()
![]() = 10 Jy. The diameter
of the source is 30''/
= 10 Jy. The diameter
of the source is 30''/![]()
![]()
![]() 3 beamwidth. From Fig. 3
we find
3 beamwidth. From Fig. 3
we find ![]() (3) = 0.70, so that from Eq. (9) and the value
G0(20
(3) = 0.70, so that from Eq. (9) and the value
G0(20![]() ) = 0.92 of Table 2 we have G(30'') =
1 - 0.70(1 - 0.92) = 0.94. The homology-corrected telescope-independent
flux is S = S'(20
) = 0.92 of Table 2 we have G(30'') =
1 - 0.70(1 - 0.92) = 0.94. The homology-corrected telescope-independent
flux is S = S'(20![]() )/ 0.94 = 10.6 Jy. A 10 Jy point-source observed
under similar conditions has the intrinsic flux S = 10/0.92 = 10.9 Jy.
)/ 0.94 = 10.6 Jy. A 10 Jy point-source observed
under similar conditions has the intrinsic flux S = 10/0.92 = 10.9 Jy.