

Up: A statistical method for
In this paper, we define and introduce a statistical method, called the 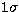 distribution function deviation test, to test assumed
distributions of sources. An example of application of the new test is also
given. The method is based on the fact that, for an assumed distribution of
sources, the variance of the distribution function of samples is
known. It is verified that, when
the random variables vary continuously, a sample passing the
test also passes any other statistical test which depends on the deviation
of a statistical function from its expected value at the
distribution function deviation test, to test assumed
distributions of sources. An example of application of the new test is also
given. The method is based on the fact that, for an assumed distribution of
sources, the variance of the distribution function of samples is
known. It is verified that, when
the random variables vary continuously, a sample passing the
test also passes any other statistical test which depends on the deviation
of a statistical function from its expected value at the
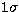 confidence level.
Specifically, in these cases, a sample passing
confidence level.
Specifically, in these cases, a sample passing
the test must also pass any
mean-value test within the same confidence level. In addition, the
sample also passes the Kolmogorov-Smirnov test at the same confidence level.
Since the mean value method and the K-S test are usually applied in the
study of the distribution of sources in astronomy, we expect that this
method will be applicable in testing the distribution of gamma-ray
bursts as well as the luminosity function of quasars.


Up: A statistical method for
Copyright The European Southern Observatory (ESO)