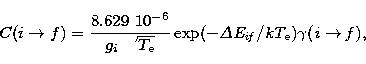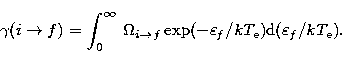Up: Electron-impact excitation rates of
Subsections
The lowest eleven states of the target ion, i.e.,
3s, 3p, 3d, 4s, 4p, 4d, 4f,
5s, 5p, 5d and 5f states, are included in the present calculation.
Each state is represented by a configuration interaction wavefunction.
The radial part of the one-electron orbitals
is expressed in the Slater form
| 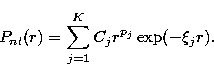 |
(1) |
The coefficients Cj and the parameters pj and 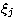 for the 1s, 2s, 2p
and 3s orbitals are
taken from the paper by Clementi & Roetti (1974),
while those for
the other orbitals are obtained with the computer code of
Hibbert (1975)
by optimizing those orbitals on the energy of the corresponding states.
for the 1s, 2s, 2p
and 3s orbitals are
taken from the paper by Clementi & Roetti (1974),
while those for
the other orbitals are obtained with the computer code of
Hibbert (1975)
by optimizing those orbitals on the energy of the corresponding states.
Excitation energies obtained in the present calculation are
compared in Table 1 with the experimental results (Moore 1971).
The excitation energies of Ar VIII are different from those of the Paper I
owing to the use of 3d orbital with three terms.
Oscillator strengths for the optically allowed transitions
from the ground state
to 3p and 4p states are shown in Table 2.
Both the excitation energies and the oscillator strengths
obtained in the present calculation are in good
agreement with those of experiment and those of other calculations.
This indicates the reliability of
the present wavefunction of the target ions.
Table 1:
Excitation energies (in Ryd) from the ground state
of the Na-like ions:
comparison of the present
calculation and
the observed values from Moore (1971) (in parentheses)
|
|
Table 2:
Oscillator strengths
|
|
The R-matrix theory of electron-ion collisions has been described
in detail by Burke & Robb (1975).
The total wavefunction
representing the electron-ion collision system is expanded
in a sphere with radius 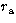 as follows:
as follows:
| 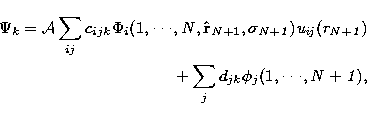 |
|
| (2) |
where 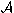 is the anti-symmetrization operator,
is the anti-symmetrization operator, 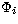 the channel
function representing the target state coupled with the spin and angular
functions for the scattering electron,
uij the continuum basis orbitals for the scattered electron,
and
the channel
function representing the target state coupled with the spin and angular
functions for the scattering electron,
uij the continuum basis orbitals for the scattered electron,
and 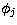 twelve-electron bound configurations formed from
fourteen bound orbitals.
Details of the basis functions uij and
twelve-electron bound configurations formed from
fourteen bound orbitals.
Details of the basis functions uij and 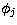 are described in
Paper I.
The coefficients cijk and djk
are determined by diagonalizing the total Hamiltonian of
the whole system with the basis set expansion defined by Eq. (2).
are described in
Paper I.
The coefficients cijk and djk
are determined by diagonalizing the total Hamiltonian of
the whole system with the basis set expansion defined by Eq. (2).
We use the computer code of Berrington et al. (1978)
to calculate the R-matrix on the boundary of the sphere,
whose radius (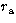 ) is taken to be 27.8, 21.0, 14.2, 11.0 and
8.8 a.u. for
Al III, Si IV, S VI,
Ar VIII and Ca X, respectively.
We include 30 continuum orbitals for each ion.
In the outer region of the sphere, a set of close-coupling equation
is solved for the partial waves L = 0-10, using the asymptotic code STGF
of Berrington et al. (1987). Contributions from the partial waves higher
than those are evaluated by using a two-state close-coupling approximation
of Henry et al. (1981) and the Coulomb-Born
approximation of Takagishi et al. (1995).
) is taken to be 27.8, 21.0, 14.2, 11.0 and
8.8 a.u. for
Al III, Si IV, S VI,
Ar VIII and Ca X, respectively.
We include 30 continuum orbitals for each ion.
In the outer region of the sphere, a set of close-coupling equation
is solved for the partial waves L = 0-10, using the asymptotic code STGF
of Berrington et al. (1987). Contributions from the partial waves higher
than those are evaluated by using a two-state close-coupling approximation
of Henry et al. (1981) and the Coulomb-Born
approximation of Takagishi et al. (1995).
Excitation rate coefficients C(in cm3 s-1)
for a transition i to f is calculated using the following
formula,
| 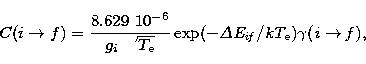 |
(3) |
where 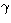 is the effective collision strength defined by
is the effective collision strength defined by
| 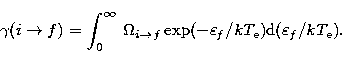 |
(4) |
Here 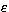 f is the energy of
the electron after the collision,
gi the statistical weight of the level
f is the energy of
the electron after the collision,
gi the statistical weight of the level 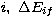 the excitation energy, and
the excitation energy, and 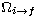 the collision strength.
The temperature
the collision strength.
The temperature 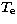 is expressed in K.
To obtain the rate coefficient at high
temperature, we fit the present collision strengths in the region where
no resonances appear to an analytic form
is expressed in K.
To obtain the rate coefficient at high
temperature, we fit the present collision strengths in the region where
no resonances appear to an analytic form
| 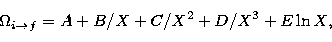 |
(5) |
where X = k2i/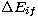 , where k2i is the
incident energy in Ryd and
, where k2i is the
incident energy in Ryd and 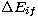 is given in Ryd.
For a dipole-allowed transition, the form is used with D = 0 and
E = 4gifif/
is given in Ryd.
For a dipole-allowed transition, the form is used with D = 0 and
E = 4gifif/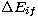 , where fif is
the oscillator strength for
, where fif is
the oscillator strength for 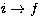 .The form (5) with E = 0 is used for optically forbidden cases.
Thus the effective collision
strength is evaluated with the collision strengths calculated in the
resonance region and with the Eq. (5) otherwise.
.The form (5) with E = 0 is used for optically forbidden cases.
Thus the effective collision
strength is evaluated with the collision strengths calculated in the
resonance region and with the Eq. (5) otherwise.


Up: Electron-impact excitation rates of
Copyright The European Southern Observatory (ESO)
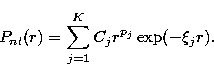
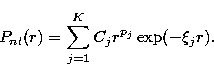
![]() as follows:
as follows:
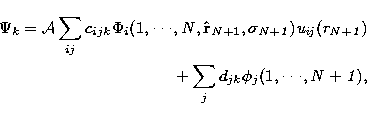
![]() ) is taken to be 27.8, 21.0, 14.2, 11.0 and
8.8 a.u. for
Al III, Si IV, S VI,
Ar VIII and Ca X, respectively.
We include 30 continuum orbitals for each ion.
In the outer region of the sphere, a set of close-coupling equation
is solved for the partial waves L = 0-10, using the asymptotic code STGF
of Berrington et al. (1987). Contributions from the partial waves higher
than those are evaluated by using a two-state close-coupling approximation
of Henry et al. (1981) and the Coulomb-Born
approximation of Takagishi et al. (1995).
) is taken to be 27.8, 21.0, 14.2, 11.0 and
8.8 a.u. for
Al III, Si IV, S VI,
Ar VIII and Ca X, respectively.
We include 30 continuum orbitals for each ion.
In the outer region of the sphere, a set of close-coupling equation
is solved for the partial waves L = 0-10, using the asymptotic code STGF
of Berrington et al. (1987). Contributions from the partial waves higher
than those are evaluated by using a two-state close-coupling approximation
of Henry et al. (1981) and the Coulomb-Born
approximation of Takagishi et al. (1995).