Up: The intraday variability in objects
The observation presented here were carried out with the one-meter telescope
of Yunnan Observatory during November 1996 to January 1997. The telescope is
equipped with a direct CCD (1024 1024 pixels) camera at the Cassergrain
focus. The CCD was bought from Princeton Instruments Company, U.S.A.
The field is about 6.5
1024 pixels) camera at the Cassergrain
focus. The CCD was bought from Princeton Instruments Company, U.S.A.
The field is about 6.5
 6.5
6.5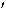 .
The filters are standard Johnson broadband filters as:
.
The filters are standard Johnson broadband filters as:
B - GG385(2 mm) + BG12(1 mm) + BG18(2 mm)
V - GG495(2 mm) + BG18(2 mm)
R - RG610(3 mm) + 66.2500(1 mm)
I - RG715(3 mm) + 60.5050(1 mm).
The exposure time is 300 - 400 seconds for B and V filters, 100 - 200 seconds
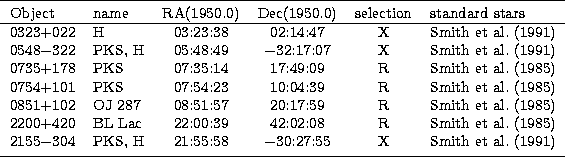
for R and I filters. The sources we observed are listed in Table 1. They
are selected arbitrarily. The standard stars in the field are taken from
Smith et al. (1985, 1991) (see Table 1).
Table 1:
The list of the sources
|
|
The results are given in Table 2. The first column is the observing date, the
second the Julian date, the third the magnitude, the fourth the observational
1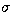 uncertainty level and the last the filter used. All observing
data were processed using the photometric tool, APPHOT, in IRAF software
package. The flat field images were taken at dusk and dawn when possible.
The bias (taken at least 15 images each night) were taken at the beginning
of the observation and the end. The source magnitude is given as the average
of those derived with respect to the two brightest standard stars in the
image frame containing the source which present the smallest variations in
their differential magnitudes. The errors quoted in Table 2 are calculated
from the two standard stars, star 1 and star 2, in the usual way,
uncertainty level and the last the filter used. All observing
data were processed using the photometric tool, APPHOT, in IRAF software
package. The flat field images were taken at dusk and dawn when possible.
The bias (taken at least 15 images each night) were taken at the beginning
of the observation and the end. The source magnitude is given as the average
of those derived with respect to the two brightest standard stars in the
image frame containing the source which present the smallest variations in
their differential magnitudes. The errors quoted in Table 2 are calculated
from the two standard stars, star 1 and star 2, in the usual way,
| 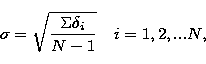 |
(1) |
where 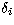 =
=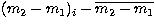 ,
m2-m1 is the differential magnitude between star 2 and star 1,
,
m2-m1 is the differential magnitude between star 2 and star 1,
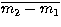 is
the mean differential magnitude, and N is the number of the observations.
Star 1, which is the brightest standard star, is also used for calibration,
and star 2 is standard star whose brightness is comparable with the source
or a little fainter than the source. When all the standard stars are
brighter than the source, the actual observational error for the source
is greater than the
is
the mean differential magnitude, and N is the number of the observations.
Star 1, which is the brightest standard star, is also used for calibration,
and star 2 is standard star whose brightness is comparable with the source
or a little fainter than the source. When all the standard stars are
brighter than the source, the actual observational error for the source
is greater than the 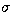 calculated as above, and the errors have been
given according to the typical uncertainties for sources of brightness
comparable with the source.
calculated as above, and the errors have been
given according to the typical uncertainties for sources of brightness
comparable with the source.


Up: The intraday variability in objects
Copyright The European Southern Observatory (ESO)