

Up: Photographic surface photometry of
Subsections
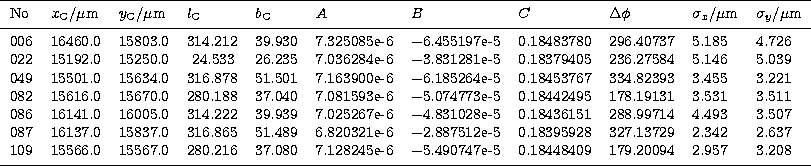
Table 2:
The coordinates of the tangential points, the parameters
of distortion and offset, and the resulting errors are
given for each image
|
|
Due to the precise manufacturing of the GAUSS camera,
its distortion can be assumed as radially symmetric with respect to the
optical axis of the system. Hence, the coordinates to describe this
distortion have been chosen as spherical ones: the radial distance
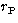 of an image point
from the center of a plane plate and
the rotation angle
of an image point
from the center of a plane plate and
the rotation angle 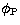 . The catalogued galactic coordinates of about
120 stars on each image have been converted into celestial spherical
coordinates: the radial distance
. The catalogued galactic coordinates of about
120 stars on each image have been converted into celestial spherical
coordinates: the radial distance 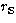 of the stars from the assumed
tangential point in the sky and the rotation angle
of the stars from the assumed
tangential point in the sky and the rotation angle 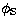 starting
from the meridian of the tangential point.
An iteration around the center point of the plate and
the estimated corresponding tangential point in the sky has been performed.
For each step the spherical celestial coordinates have been compared
with the spherical
plate coordinates, a polynomial has been fitted to the data, and the deviation
has been computed. This deviation has been minimized by the iteration
resulting in the correct coordinates
(
starting
from the meridian of the tangential point.
An iteration around the center point of the plate and
the estimated corresponding tangential point in the sky has been performed.
For each step the spherical celestial coordinates have been compared
with the spherical
plate coordinates, a polynomial has been fitted to the data, and the deviation
has been computed. This deviation has been minimized by the iteration
resulting in the correct coordinates
(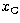 ,
, 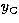 ,
, 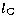 ,
, 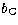 ) of the
tangential point, and in the polynomials
) of the
tangential point, and in the polynomials
| 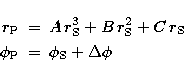 |
(1) |
| (2) |
describing the distortion and the angular offset of the camera.
The parameters for the selected images
are given in Table 2. The mean error of this rectification
is about 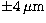 or
or 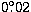 in the sky.
in the sky.
Table 3:
The calibration parameters are given for each image
|
|
The former Bochum surface photometries (Paper VII; Paper VIII) have been
calibrated by the mean of gradation curves that have been exposed
using ESO's wedge spectrograph ETA. Additionally, during the photographic
exposures absolute calibration data and information on airglow, scattered
light and extinction have been measured photoelectrically.
Since none of these measurements has been done during the spacebound
observation, the gradation curves had to be reconstructed from the
images themselves. This requires measuring the star densities
to compare them with their catalogued fluxes. As reference, the catalogues
of Jamar et al. (1976) and of
Thompson et al. (1978) have been taken, both
resulting from the measurements of the satellite TD1. The stars have been
identified on the images, the maximum of their
density has been determined, and for all recovered stars (about 1500 on
each image) these maxima have
been set in relation to the catalogued flux. The transformation from the
measured densities to relative intensities were done by using the
characteristic curve after Moffat (1969)
| 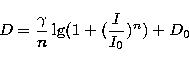 |
(3) |
where D is the measured density, and D0 the density of the chemical
fog of the photograph. 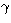 , n and I0 are free
parameters that have been derived by fitting the curve to the data.
The typical mean error of this calibration is about 2%.
, n and I0 are free
parameters that have been derived by fitting the curve to the data.
The typical mean error of this calibration is about 2%.
Absolute calibration was obtained by integrating the relative
photographic intensities of each identified star, subtracting its
individual sky background, and comparing the resulting
aperture star photometries 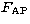 with the catalogued fluxes F*. This yields a linear relation
with a typical mean error of about 3%.
with the catalogued fluxes F*. This yields a linear relation
with a typical mean error of about 3%.
To obtain the surface photometries, the calibrated images have been
divided by 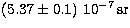 which is the mean area of
one pixel.
The parameters D0,
which is the mean area of
one pixel.
The parameters D0, 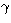 , n and I0 of the relative calibration,
the ratio
, n and I0 of the relative calibration,
the ratio 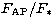 describing the absolute calibration,
and the resulting mean error
are given in Table 3 for each image.
describing the absolute calibration,
and the resulting mean error
are given in Table 3 for each image.
The elimination of disturbing, individual foreground stars has been
done in two steps. First, all stars brighter than
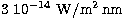 have been removed from the images.
These stars have a characteristic intensity profile that has been
used for their identification.
Beginning in the center of each star, the average radial differences
have been computed and compared to the inner error. As soon as the
difference became smaller than the mean error, the hereto belonging
circle was defined
as the "edge'' of the star and the intensity inside this circle was replaced by
the average of the individual background.
have been removed from the images.
These stars have a characteristic intensity profile that has been
used for their identification.
Beginning in the center of each star, the average radial differences
have been computed and compared to the inner error. As soon as the
difference became smaller than the mean error, the hereto belonging
circle was defined
as the "edge'' of the star and the intensity inside this circle was replaced by
the average of the individual background.
The fainter stars which do not have this characteristic profile do
only cover an area of maximally four pixel and could be removed by
a filter similar to the one described in
Paper VII. Herewith, all stars brighter than 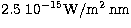 have finally been eliminated from the images.
have finally been eliminated from the images.
To correct for zodiacal light, we used the values published by
Tennyson et al. (1988). Since the zodiacal light
at 217nm and 280nm
is distributed quite homogeneously (Murthy et al. 1990),
and since its
intensity is also very small,
it is sufficient
to substract an average value from each image. This value has been determined
to 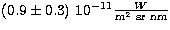 at 217nm and
to
at 217nm and
to 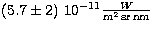 at 280nm.
at 280nm.
Much stronger is the additional light emission that is produced by the shuttle
while interacting with the upper atmosphere.
Many of the images are influenced by
these shuttle glow effects (see Jütte 1996 for a thorough
investigation of these phenomena).
The classical Shuttle Glow is generally considered to be
relatively strong in the red and
near-infrared passbands but negligible in the UV. However,
we have detected quite intense light phenomena at shorter wavelengths that
seem to be related to the shuttle:
large, bright clouds surrounding the shuttle and even the camera itself.
They seem to be of variable origin and
change on timescales of seconds to hours.
To eliminate these clouds from the images, they have been fitted with
twodimensional polynomials of fourth order. These fits reproduced the shape
of the clouds in a reasonable way, however, the zero point of the sky
background could not be derived by this method. Therefore it has been estimated
from the darkest parts of the images, which have been regarded as unaffected
by the glow. The error of this estimation is very high with about 20% of the
mean Milky Way brightness. However, there is no other possibility to derive
the correct sky background. We consider these glow phenomena to be a major
obstacle to all photometries obtained at Low Earth Orbits.
The derivation of the geometric parameters (Table 2)
allows the transformation of the images into maps of the Milky Way
in cartesian coordinates l, b. The stepsize has been chosen as
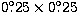 for comparison with the
for comparison with the  photometries
(Paper VII; Paper VIII). The individual maps have been added up to give
a picture of the Milky Way by averaging the overlapping regions.
Due to the small number of usable images, there are only a few regions
where the sky coverage is equal or better than three images (see Fig. 3).
photometries
(Paper VII; Paper VIII). The individual maps have been added up to give
a picture of the Milky Way by averaging the overlapping regions.
Due to the small number of usable images, there are only a few regions
where the sky coverage is equal or better than three images (see Fig. 3).
 |
Figure 3:
The number of images that have been averaged
for each point of the final maps (above: 280nm; below: 217nm) |


Up: Photographic surface photometry of
Copyright The European Southern Observatory (ESO)

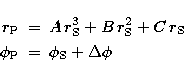
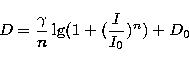
![]() with the catalogued fluxes F*. This yields a linear relation
with a typical mean error of about 3%.
with the catalogued fluxes F*. This yields a linear relation
with a typical mean error of about 3%.
![]() which is the mean area of
one pixel.
The parameters D0,
which is the mean area of
one pixel.
The parameters D0, ![]() , n and I0 of the relative calibration,
the ratio
, n and I0 of the relative calibration,
the ratio ![]() describing the absolute calibration,
and the resulting mean error
are given in Table 3 for each image.
describing the absolute calibration,
and the resulting mean error
are given in Table 3 for each image.
![]() have finally been eliminated from the images.
have finally been eliminated from the images.
