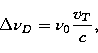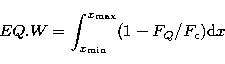Up: A series of theoretical components
We have assumed a spherical shape of the reflecting atmosphere to
simplify the computational problems of radiative transfer.
The geometry of the model is
shown in Fig. 1.
![\begin{figure}
\centering
\includegraphics[width=8.8cm]{ds1378f1.eps}\end{figure}](/articles/aas/full/1998/16/ds1378/Timg7.gif) |
Figure 1:
Schematic diagram of the binary components with incident
radiation from the surface of the secondary. O and 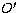 are the
centres of gravity of the two components are the
centres of gravity of the two components |
Let O and 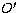 be the centres of the primary and the secondary respectively. The
atmosphere of the primary is assumed to be spherical and divided into
several discrete shells. We calculate the source functions of the radiation
field emerging from the companion whose centre is at
be the centres of the primary and the secondary respectively. The
atmosphere of the primary is assumed to be spherical and divided into
several discrete shells. We calculate the source functions of the radiation
field emerging from the companion whose centre is at 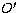 (see Fig. 1)
and incident on the atmosphere of the component whose centre is at O. We
consider the set of rays such as STP,
(see Fig. 1)
and incident on the atmosphere of the component whose centre is at O. We
consider the set of rays such as STP, 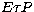 ,
, 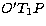 ,
,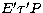 , WT2P etc., emerging from the surface SW
of the companion and meeting at
a point P in the atmospheres of the component. These rays lie within the
quadrilateral such as
, WT2P etc., emerging from the surface SW
of the companion and meeting at
a point P in the atmospheres of the component. These rays lie within the
quadrilateral such as 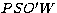 and enter the boundary of the atmosphere of the
component at points
and enter the boundary of the atmosphere of the
component at points 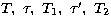 etc. The surfaces of the
companion such as SW will be different for different points P in the
atmosphere.
The radiation field at P is estimated by calculating the source
function whose
contribution comes from self radiation of the primary and that due to the
incident radiation from the surface SW of the secondary facing the primary.
We need to estimate geometrical length of the ray segments such as
etc. The surfaces of the
companion such as SW will be different for different points P in the
atmosphere.
The radiation field at P is estimated by calculating the source
function whose
contribution comes from self radiation of the primary and that due to the
incident radiation from the surface SW of the secondary facing the primary.
We need to estimate geometrical length of the ray segments such as 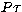 ,
,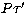 etc,
inside the atmosphere so that the transfer of radiation along these segments
is estimated and
its contribution to the source function at the point P due to the
incident radiation at
etc,
inside the atmosphere so that the transfer of radiation along these segments
is estimated and
its contribution to the source function at the point P due to the
incident radiation at 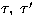 etc. The length of the segments
such as
etc. The length of the segments
such as
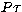 in
in 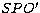 are given in the Appendix A
(see Peraiah 1983 and
Peraiah & Rao 1983).
are given in the Appendix A
(see Peraiah 1983 and
Peraiah & Rao 1983).
For a given density distribution we need to calculate the optical depth
along the segments 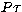 ,
, 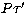 etc. The source function at
points such as P due to the irradiation are calculated using the
one-dimensional transfer (Wing 1962;
Sobolev 1963; Grant 1968). We will
describe this procedure briefly below.
etc. The source function at
points such as P due to the irradiation are calculated using the
one-dimensional transfer (Wing 1962;
Sobolev 1963; Grant 1968). We will
describe this procedure briefly below.
![\begin{figure}
\centering
\includegraphics[width=8.8cm]{ds1378f2.eps}\end{figure}](/articles/aas/full/1998/16/ds1378/Timg17.gif) |
Figure 2:
Schematic diagram of the rod model |
We consider a segment AB (see Fig 2) which has two rays oppositely directed
to each other. The optical depth 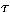 is given by,
is given by,
| 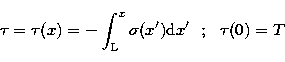 |
(1) |
where 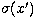 is the extinction coefficient and T is the
total optical depth. The optical depth is measured in the direction opposite to that
of the geometrical segment.
is the extinction coefficient and T is the
total optical depth. The optical depth is measured in the direction opposite to that
of the geometrical segment.
We assume a steady state, monochromatic condition with local source
function 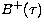 in the direction of increasing
in the direction of increasing 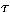 and
and  in the reverse direction.
in the reverse direction. 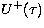 and
and 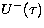 are the
specific intensities in the
are the
specific intensities in the 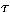 increasing and decreasing directions
respectively.
increasing and decreasing directions
respectively.
The two equations of transfer for 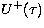 and
and 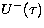 are
are
| 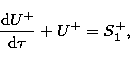 |
(2) |
| 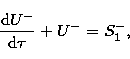 |
(3) |
where
| ![\begin{displaymath}
S_1^+ = B^+ (\tau) + \omega (\tau) \bigl [p (\tau) U^+(\tau) + (1 - p (\tau) U^-
(\tau)\bigr], \end{displaymath}](/articles/aas/full/1998/16/ds1378/img27.gif) |
(4) |
| ![\begin{displaymath}
S_1^- = B^- (\tau) + \omega(\tau) \bigl [(1 - p (\tau)) U^+ (\tau) + p(\tau) U^-
(\tau)\bigr],\end{displaymath}](/articles/aas/full/1998/16/ds1378/img28.gif) |
(5) |
are the source functions and 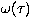 is the albedo for
single scattering and the phase function
is the albedo for
single scattering and the phase function 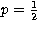 .
The boundary conditions at
.
The boundary conditions at 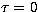 and
and 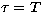 are given by
are given by
| 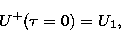 |
(6) |
|  |
(7) |
where U1 and U2 will be specified later. The total source function 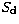 at any point
at any point 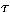 is the combination of the scattered part of the local
intensities
is the combination of the scattered part of the local
intensities 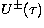 in either directions and the diffuse radiation
generated by the incident radiation at the boundaries
in either directions and the diffuse radiation
generated by the incident radiation at the boundaries  and
and  (the quantities U1 and U2 in Eqs. (6) and (7) respectively).
This added to the local sources would give the total source function given
by,
(the quantities U1 and U2 in Eqs. (6) and (7) respectively).
This added to the local sources would give the total source function given
by,
| ![\begin{eqnarray}
S^+_{\rm d} (\tau){=}S_1^+\! (\tau)\! +\! \omega (\tau)\!
\big...
...u}
\!\!+\! p (\tau) U_{2} {\rm e}^{-(T - \tau)}\bigg]\nonumber\\ \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img37.gif) |
|
| (8) |
| |
In this case, the boundary conditions are,
We can write the Eqs. (2) and (3) as
|  |
(10) |
where
| ![\begin{displaymath}
{M}=
\left[
\begin{array}
{ll}
1 & 0 \\ 0 & -1 \end{array...
...
\left[
\begin{array}
{l}
S_1^+ \\ S_1^- \end{array}\right],\end{displaymath}](/articles/aas/full/1998/16/ds1378/img39.gif) |
(11) |
and Eqs. (4) and (5) and (8) and (9) will be written as,
| 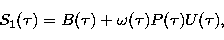 |
(12) |
| 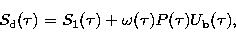 |
(13) |
where
| ![\begin{displaymath}
{B}=
\left[
\begin{array}
{l}
B^+ \\ B^- \end{array}\righ...
...ft[
\begin{array}
{ll}
p & 1-p \\ 1-p & p\end{array}\right],\end{displaymath}](/articles/aas/full/1998/16/ds1378/img42.gif) |
(14) |
| ![\begin{displaymath}
{U_{\rm b}(\tau)}=
\left[
\begin{array}
{ll}
U_1 & {\rm e}^{-\tau} \\ U_2 & {\rm e}^{-(T-\tau)} \end{array}\right].\end{displaymath}](/articles/aas/full/1998/16/ds1378/img43.gif) |
(15) |
The mathematical aspects of the solution of the Eqs. (2) and (3) are
discussed in Sobolev (1963) and Grant (1968). We shall merely quote the
relevant results and these are given in Appendix B.
Using equations (B1) and (B2) one can calculate the source function at
points such as P, due to the incident radiation from the secondary component.
Now, we need to estimate the source function due to self radiation of the
component. This can be done by solving the line transfer equation for a
Non-LTE two-level atom in the comoving frame in spherical symmetry. This
is given by (see Peraiah 1984; Peraiah et al. 1987)
| ![\begin{eqnarray}
& & \mu \frac {\partial I(x, \mu, r)}{\partial r} + \frac {(1 -...
...} {{\rm d}r}\bigg]
\frac {\partial I (x, \mu, r)} {\partial x}, \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img44.gif) |
|
| |
| (16) |
and
| ![\begin{eqnarray}
& & -\mu \frac {\partial I (x, -\mu, r)} {\partial r} - \frac {...
...} {{\rm d}r} \bigg] \frac {\partial I (x, -\mu, r)} {\partial x}, \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img45.gif) |
|
| |
| |
| (17) |
where  is the specific intensity of the ray
at an angle
is the specific intensity of the ray
at an angle ![$\cos^{-1} \mu \ \ [\mu \epsilon (0, 1)]$](/articles/aas/full/1998/16/ds1378/img47.gif) with the radius vector at
the radial point r with frequency
with the radius vector at
the radial point r with frequency 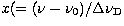 where
where
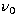 and
and 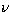 are the frequency points at the line centre and at any
point in the line and
are the frequency points at the line centre and at any
point in the line and 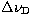 is the standard frequency interval
such as Doppler width) V(r) is the velocity of the gas at r in units of
mean thermal units (mtu) and K(x, r) and
is the standard frequency interval
such as Doppler width) V(r) is the velocity of the gas at r in units of
mean thermal units (mtu) and K(x, r) and 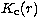 are the absorption
coefficients per unit frequency interval in the line and the continuum
respectively. The quantities
are the absorption
coefficients per unit frequency interval in the line and the continuum
respectively. The quantities 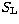 and
and 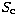 are the line and continuum
source functions given by,
are the line and continuum
source functions given by,
| 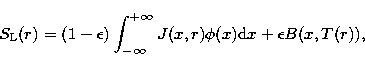 |
(18) |
|  |
(19) |
| 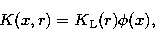 |
(20) |
where 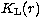 is the line-centre absorption coefficient and
is the line-centre absorption coefficient and
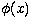 is the normalized line profile and
is the normalized line profile and 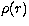 is an arbitrary
factor less than one and B(x, T(r)) is the Planck function with frequency
x, and temperature T at the radial point r. J(x, r) is the mean intensity given by,
is an arbitrary
factor less than one and B(x, T(r)) is the Planck function with frequency
x, and temperature T at the radial point r. J(x, r) is the mean intensity given by,
| 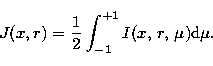 |
(21) |
The quantity 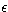 is the probability per scattering that a photon
is thermalised by collisional de-excitation of the excited states, and this
is given by,
is the probability per scattering that a photon
is thermalised by collisional de-excitation of the excited states, and this
is given by,
| ![\begin{displaymath}
\epsilon=C_{21} \bigg [C_{21}+A_{21} \bigl [1-\exp (-h \nu_{0}/ kT)\bigr ] \bigg ]^{-1}\end{displaymath}](/articles/aas/full/1998/16/ds1378/img63.gif) |
(22) |
where C21 is the collisional transition rate from level 2 to 1 and
A21 is the Einstein spontaneous emission probability for transition from
level 2 to 1. The quantities h and k are the Planck constant and Boltzmann
constant respectively. From
Eqs. (17) to (22), we obtain the source function due to self
radiation, given by
| 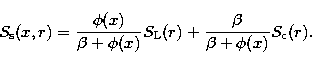 |
(23) |
where 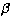 is the ratio of absorption coefficients in the
continuum and line
centre.
is the ratio of absorption coefficients in the
continuum and line
centre.
Finally we calculate the total source function
by adding 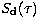 in
Eq. (14) and
in
Eq. (14) and  in Eq. (24) and obtain,
in Eq. (24) and obtain,
| 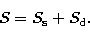 |
(24) |
We calculate the set of source functions at the points of intersection
of the ray parallel to the line of sight and the shell boundaries. These
source functions are used to calculate the emergent specific intensities
at infinity (or at the observer's point), by using the formula
(see Peraiah & Srinivasa Rao 1983)
| ![\begin{displaymath}
I_{n+1} (r) = I_0(n) {\rm e}^{-\tau} + \int_o^\tau S(t)
{\rm e}^{-[-(\tau - t)]}{\rm d}t,\end{displaymath}](/articles/aas/full/1998/16/ds1378/img68.gif) |
(25) |
where In(r) corresponds to the specific intensity of the ray
passing through shell numbers n and n+1 and corresponding to
the perpendicular
to the axis 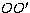 at different radii. I0(n) corresponds to
the incident intensity at the boundary of the shell and
at different radii. I0(n) corresponds to
the incident intensity at the boundary of the shell and 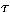 is the
optical depth in the sector along the ray path. The source function
S(t) is calculated by linear interpolation between S(tn) and
S(tn+1). The specific intensity at the boundary of each shell is
calculated by using Eq. (26).
is the
optical depth in the sector along the ray path. The source function
S(t) is calculated by linear interpolation between S(tn) and
S(tn+1). The specific intensity at the boundary of each shell is
calculated by using Eq. (26).
The atmosphere in question is divided in to n shells (see Fig. 1)
where n = 1
corresponds 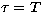 and n = 100 corresponding to
and n = 100 corresponding to 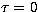 , and
, and
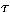 is the optical depth at any point
and T is the total optical depth. The total optical depth is set in advance.
The incident radiation at Q, the bottom of the
atmosphere, (see Fig. 1) is given as
is the optical depth at any point
and T is the total optical depth. The total optical depth is set in advance.
The incident radiation at Q, the bottom of the
atmosphere, (see Fig. 1) is given as
| 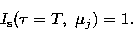 |
(26) |
The incident radiation from the secondary is given in terms
of 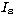 in the ratio I, where I is given by
in the ratio I, where I is given by
| 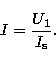 |
(27) |
The velocities of expansion of the gas are expressed in terms of mean thermal
units VT (mtu) given by,
| ![\begin{displaymath}
V_{T} = \bigg [{\frac {2kT} {m_i} } \bigg ] ^ {\frac {1} {2} }\end{displaymath}](/articles/aas/full/1998/16/ds1378/img73.gif) |
(28) |
where k is the Boltzmann constant and T is the temperature and mi is the
mass of the ion. The velocity at n=1 or 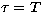 is VA and VB is the velocity at
n = 100 or
is VA and VB is the velocity at
n = 100 or 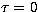 are given in terms of mtu or VT as
are given in terms of mtu or VT as
| 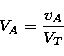 |
(29) |
| 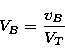 |
(30) |
where vA and vB are the velocities at the inner radius A, outer radius
B at radial point r respectively in units of mtu of gas.
We assume uniform expansion of the gases for the sake of simplicity.
The proximity of the component
is measured in terms of separation parameter
r1/R, where r1 is the radius of the primary and R is the
separation of
centres of gravity of the two components.
The ratio of the outer to the inner radii (B/A) of the atmosphere is
always taken to be 2. The actual thickness in the components could be much
larger than what we have considered here. As the number of parameters is
large, we restricted our calculations to this modest thickness of the atmosphere.
The variation of the source functions are shown against the shell numbers
(n = 1 to 100) for different parameters are shown. The line
profile fluxes 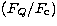 are plotted against
the normalized frequency Q,
where
are plotted against
the normalized frequency Q,
where
| 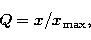 |
(31) |
| 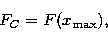 |
(33) |
and
| 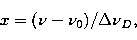 |
(34) |
| 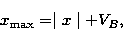 |
(35) |
| 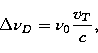 |
(36) |
x lies between 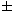 5 units. The equivalent widths are calculated by the relation,
5 units. The equivalent widths are calculated by the relation,
| 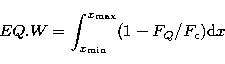 |
(37) |
where
| 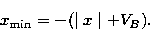 |
(38) |


Up: A series of theoretical components
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\centering
\includegraphics[width=8.8cm]{ds1378f1.eps}\end{figure}](/articles/aas/full/1998/16/ds1378/Timg7.gif)
![\begin{figure}
\centering
\includegraphics[width=8.8cm]{ds1378f1.eps}\end{figure}](/articles/aas/full/1998/16/ds1378/Timg7.gif)
![]() be the centres of the primary and the secondary respectively. The
atmosphere of the primary is assumed to be spherical and divided into
several discrete shells. We calculate the source functions of the radiation
field emerging from the companion whose centre is at
be the centres of the primary and the secondary respectively. The
atmosphere of the primary is assumed to be spherical and divided into
several discrete shells. We calculate the source functions of the radiation
field emerging from the companion whose centre is at ![]() (see Fig. 1)
and incident on the atmosphere of the component whose centre is at O. We
consider the set of rays such as STP,
(see Fig. 1)
and incident on the atmosphere of the component whose centre is at O. We
consider the set of rays such as STP, ![]() ,
, ![]() ,
,![]() , WT2P etc., emerging from the surface SW
of the companion and meeting at
a point P in the atmospheres of the component. These rays lie within the
quadrilateral such as
, WT2P etc., emerging from the surface SW
of the companion and meeting at
a point P in the atmospheres of the component. These rays lie within the
quadrilateral such as ![]() and enter the boundary of the atmosphere of the
component at points
and enter the boundary of the atmosphere of the
component at points ![]() etc. The surfaces of the
companion such as SW will be different for different points P in the
atmosphere.
The radiation field at P is estimated by calculating the source
function whose
contribution comes from self radiation of the primary and that due to the
incident radiation from the surface SW of the secondary facing the primary.
We need to estimate geometrical length of the ray segments such as
etc. The surfaces of the
companion such as SW will be different for different points P in the
atmosphere.
The radiation field at P is estimated by calculating the source
function whose
contribution comes from self radiation of the primary and that due to the
incident radiation from the surface SW of the secondary facing the primary.
We need to estimate geometrical length of the ray segments such as ![]() ,
,![]() etc,
inside the atmosphere so that the transfer of radiation along these segments
is estimated and
its contribution to the source function at the point P due to the
incident radiation at
etc,
inside the atmosphere so that the transfer of radiation along these segments
is estimated and
its contribution to the source function at the point P due to the
incident radiation at ![]() etc. The length of the segments
such as
etc. The length of the segments
such as
![]() in
in ![]() are given in the Appendix A
(see Peraiah 1983 and
Peraiah & Rao 1983).
are given in the Appendix A
(see Peraiah 1983 and
Peraiah & Rao 1983).
![]() ,
, ![]() etc. The source function at
points such as P due to the irradiation are calculated using the
one-dimensional transfer (Wing 1962;
Sobolev 1963; Grant 1968). We will
describe this procedure briefly below.
etc. The source function at
points such as P due to the irradiation are calculated using the
one-dimensional transfer (Wing 1962;
Sobolev 1963; Grant 1968). We will
describe this procedure briefly below.
![]() is given by,
is given by,
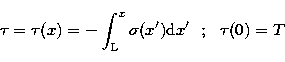
![]() is the extinction coefficient and T is the
total optical depth. The optical depth is measured in the direction opposite to that
of the geometrical segment.
is the extinction coefficient and T is the
total optical depth. The optical depth is measured in the direction opposite to that
of the geometrical segment.
![]() in the direction of increasing
in the direction of increasing ![]() and
and ![]() in the reverse direction.
in the reverse direction. ![]() and
and ![]() are the
specific intensities in the
are the
specific intensities in the ![]() increasing and decreasing directions
respectively.
increasing and decreasing directions
respectively.
![]() and
and ![]() are
are
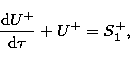
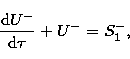
![]() is the albedo for
single scattering and the phase function
is the albedo for
single scattering and the phase function ![]() .
The boundary conditions at
.
The boundary conditions at ![]() and
and ![]() are given by
are given by
![\begin{eqnarray}
S^+_{\rm d} (\tau){=}S_1^+\! (\tau)\! +\! \omega (\tau)\!
\big...
...u}
\!\!+\! p (\tau) U_{2} {\rm e}^{-(T - \tau)}\bigg]\nonumber\\ \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img37.gif)

![\begin{displaymath}
{M}=
\left[
\begin{array}
{ll}
1 & 0 \\ 0 & -1 \end{array...
...
\left[
\begin{array}
{l}
S_1^+ \\ S_1^- \end{array}\right],\end{displaymath}](/articles/aas/full/1998/16/ds1378/img39.gif)
![\begin{displaymath}
{B}=
\left[
\begin{array}
{l}
B^+ \\ B^- \end{array}\righ...
...ft[
\begin{array}
{ll}
p & 1-p \\ 1-p & p\end{array}\right],\end{displaymath}](/articles/aas/full/1998/16/ds1378/img42.gif)
![\begin{displaymath}
{U_{\rm b}(\tau)}=
\left[
\begin{array}
{ll}
U_1 & {\rm e}^{-\tau} \\ U_2 & {\rm e}^{-(T-\tau)} \end{array}\right].\end{displaymath}](/articles/aas/full/1998/16/ds1378/img43.gif)
![\begin{eqnarray}
& & \mu \frac {\partial I(x, \mu, r)}{\partial r} + \frac {(1 -...
...} {{\rm d}r}\bigg]
\frac {\partial I (x, \mu, r)} {\partial x}, \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img44.gif)
![\begin{eqnarray}
& & -\mu \frac {\partial I (x, -\mu, r)} {\partial r} - \frac {...
...} {{\rm d}r} \bigg] \frac {\partial I (x, -\mu, r)} {\partial x}, \end{eqnarray}](/articles/aas/full/1998/16/ds1378/img45.gif)
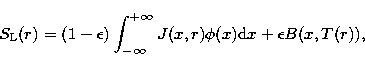
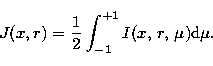
![\begin{displaymath}
\epsilon=C_{21} \bigg [C_{21}+A_{21} \bigl [1-\exp (-h \nu_{0}/ kT)\bigr ] \bigg ]^{-1}\end{displaymath}](/articles/aas/full/1998/16/ds1378/img63.gif)
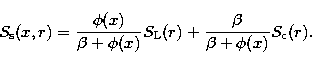
![]() in
Eq. (14) and
in
Eq. (14) and ![]() in Eq. (24) and obtain,
in Eq. (24) and obtain,
![\begin{displaymath}
I_{n+1} (r) = I_0(n) {\rm e}^{-\tau} + \int_o^\tau S(t)
{\rm e}^{-[-(\tau - t)]}{\rm d}t,\end{displaymath}](/articles/aas/full/1998/16/ds1378/img68.gif)
![]() and n = 100 corresponding to
and n = 100 corresponding to ![]() , and
, and
![]() is the optical depth at any point
and T is the total optical depth. The total optical depth is set in advance.
The incident radiation at Q, the bottom of the
atmosphere, (see Fig. 1) is given as
is the optical depth at any point
and T is the total optical depth. The total optical depth is set in advance.
The incident radiation at Q, the bottom of the
atmosphere, (see Fig. 1) is given as
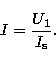
![\begin{displaymath}
V_{T} = \bigg [{\frac {2kT} {m_i} } \bigg ] ^ {\frac {1} {2} }\end{displaymath}](/articles/aas/full/1998/16/ds1378/img73.gif)
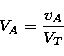
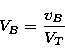
![]() are plotted against
the normalized frequency Q,
where
are plotted against
the normalized frequency Q,
where