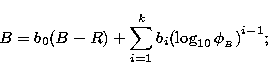
Standard magnitudes from Paper I and logarithm of photographic flux
were related by fitting a polynomial with a linear colour term. Since
our deepest plates are in R and B bands, we used the colour index
B-R for the transformation equations:
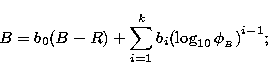 |
(1) |
 |
(2) |
 |
(3) |
![\begin{figure}
\centering
\includegraphics[width=8.6cm]{ds7458f1.eps}\end{figure}](/articles/aas/full/1998/14/ds7458/Timg34.gif) |
Figure 1: Relation among logarithm of flux and standard magnitude for the third threshold of each plate selected for deriving photographic photometry |
 |
In order to apply the above transformations to non-standard stars, a cross-identification among the different photometric plates is needed. The standard magnitudes are calculated, for a given star, following these steps:
First, as can be easily deduced from Eqs. (1) and (3), the standard R magnitude can be computed from the expression
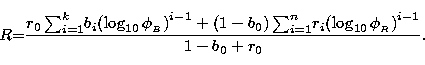
The second step, the determination of standard B magnitudes, is somewhat simpler, because only one photometric plate is used, and because the standard R value has been already computed and can be used in the calculation. From Eqs. (1) and (3) we see that B is obtained as:
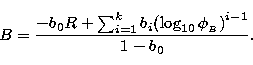
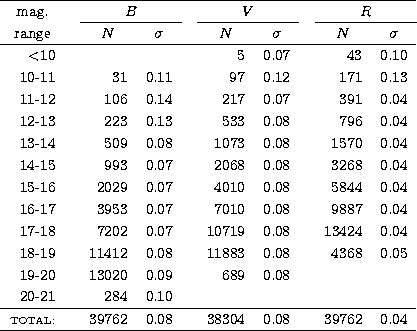
The final photometric catalogue (Table 6, available only
in electronic form) contains a total number of 39762 stars, 38304 having
complete BVR photographic photometry, and 1458 only BR
photographic photometry. The stars are designated by their
identification number on the master plate OCA 3305. Table
4 gives the number of stars by interval of magnitude in
each band.
|
The absolute accuracy of the photographic photometry is limited by
several factors. One of them is the emulsion and developing uniformity.
Since our photometric standards are located in the center of the scanned
zones, the photometric calibration would be strictly valid only in this
area. But we extrapolated the calibrations and applied them to the
whole ![]() region. We have no means of
evaluating the possible existence of photometric inhomogeneities on the
photometric plates, but visual inspection of them shows an apparent good
regularity of emulsions and developing.
region. We have no means of
evaluating the possible existence of photometric inhomogeneities on the
photometric plates, but visual inspection of them shows an apparent good
regularity of emulsions and developing.
Another source of error arises from the quality of the original CCD photometry used for the calibration. We have no reason to suspect systematic effects in the CCD data. We refer to Paper I for a detailed discussion of them.
Further uncertainties may be caused by the transformation from the effective band defined by the emulsion/filter combinations to the standard system. This effect is taken into account to some extent by means of the colour term introduced in the transformation equations. The effect of the colour term coefficients was small in all cases, and introducing further colour terms (quadratic, and so on) in the transformation equations did not improve the goodness of the fits.
The non-linearity of the photographic response is well corrected by using the appropriate polynomial degree in the transformation. The ultimate limit of accuracy lies in the intrinsic precision of the photographic emulsion. For these reasons, it is usually difficult to reach precisions better than 0.1 mag in photographic photometry. The average standard deviations of the residuals of the photometric fits (Table 3) seem to indicate that we have reached, or even improved, this limit.
In order to estimate the quality of our photographic photometry as a
function of magnitude, we compared the obtained BVR values with
the whole photometric catalogue from Paper I. As explained, a subsample
of around 400 of these stars were used as secondary standard for the calibration,
but the comparison with the whole set allows a better determination of
the photometric uncertainties as a function of magnitude.
Figure 2 displays the results of the comparison. Table
4 includes the standard deviations of the differences
CCD-photographic in one magnitude bins and
applying a 3![]() clipping to the data in
each interval. The differences contain contributions as from
photographic and from CCD photometric errors, but the second are small
compared to the first ones.
clipping to the data in
each interval. The differences contain contributions as from
photographic and from CCD photometric errors, but the second are small
compared to the first ones.
Just for cross-identification purposes, for every plate and threshold we performed a least squares fit of magnitude as a function of logarithm of flux without colour terms. The fitted model was a polynomial, and the standard stars were those used in Sect. 3.1. These polynomials were applied to all the detected objects and the different magnitudes coming from different thresholds in the same plate were averaged using as weight the object area at each threshold.
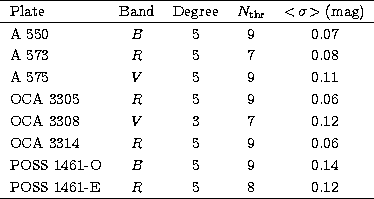
The reference bands for these raw magnitude calibrations were selected in accordance with each plate/emulsion characteristics. Johnson's B magnitude was used for non-filtered plates (Tautenburg, Heidelberg) and for B-like filtered plates (A 550, POSS 1461-O). For AC plates, the photographic magnitude values quoted in the original plate measurements were used directly. The instrumental PDS magnitudes from Shanghai plates were transformed into Johnson's B magnitude fitting a 2nd degree polynomial using the B-CCD measurements as reference. Although our master plate (OCA 3305) matches the R band, we performed a raw calibration also into Johnson's B filter, in order to allow the cross-identification with B-like plates.
R-like plates (the master plate OCA 3305, OCA 3314, A 573 and POSS 1461-E) were fitted in a similar way to the standard Cousins' R band. V-like plates (OCA 3308 and A 575) were fitted, for comparison purposes, with Cousins' R band, and this raw R magnitude was used to perform their cross-identification with the master plate. When there was cross-identification of the CCD pseudo-plate with the master plate, the R magnitude from Paper I was compared to the raw R magnitude computed in the master plate.
Several stars were saturated in some or all plates. These objects were maintained in the files, labelled as "bright'', and they received a special treatment in the cross-identification procedures.
Copyright The European Southern Observatory (ESO)