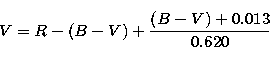Up: Stellar disks and embedded
Subsections
In this case, the analysis procedure follows two modes,
depending on whether the
disk is completely embedded in the bulge or whether it is
dominant in the outer parts.
As already mentioned, the decomposition method applied here is a modified version of the
method described in Scorza & Bender (1995). In the latter work
it was found that the modeling of twelve early-type galaxies required
disk models with profiles departing from the exponential
behaviour. These were constructed by adding several exponential
functions, most frequently two exponentials were required. In the
present work we have developed an automatized method to determine the
optimal flux intensities of the disk models without constraints on the
shapes of the disk profiles. As a first step, the initial values of an
exponential disk model were guessed as described in Scorza
& Bender (1995).
The models are described by a central surface brightness SB0,
a scale length  and an inclination angle
and an inclination angle  .
After subtraction of this input disk model (convolved to the appropriate
seeing) from the galaxy
image, an isophote analysis of the remaining bulge was carried
out. This analysis yielded, among several other parameters, the a4/a
amplitudes along the major axis. The radial flux of the input disk
model was then corrected according to the amplitude of the remaining
a4/a signature of the bulge via:
.
After subtraction of this input disk model (convolved to the appropriate
seeing) from the galaxy
image, an isophote analysis of the remaining bulge was carried
out. This analysis yielded, among several other parameters, the a4/a
amplitudes along the major axis. The radial flux of the input disk
model was then corrected according to the amplitude of the remaining
a4/a signature of the bulge via:
| 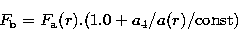 |
(1) |
where  is the initial flux,
is the initial flux,  the corrected one and r
the radius. With this corrected flux profile, a new disk model was
constructed and subtracted from the galaxy image. The procedure was
repeated until the isophotes of the bulge show a4/a
the corrected one and r
the radius. With this corrected flux profile, a new disk model was
constructed and subtracted from the galaxy image. The procedure was
repeated until the isophotes of the bulge show a4/a  . If
it was found that the iteration did fail to converge properly, an input
disk model with either a higher or a lower surface brightness was
used.
. If
it was found that the iteration did fail to converge properly, an input
disk model with either a higher or a lower surface brightness was
used.
Simulations of the decomposition procedure with perfect galaxy models
showed that both input disks with too high or too low
surface brightness did converge to the true disk. However,
the convergence
from brighter input disk models was in general better than from fainter
input disks.
In the present version of the method the surface brightness profile of
the disk is left free and can take any shape, provided that after
disk subtraction the remaining bulge shows elliptical isophotes.
The
method described so far gave satisfactory results for objects with
embedded disks (case I in Sect. 3).
In case of a boxy bulge (case I.b) the disk profile was
modified in such way that after disk subtraction,
the remaining bulge showed also boxy
isophotes and therefore negative a4/4 values
(e.g. see the case of NGC 3818, Fig. A15 in the Appendix).
If the disk was found to dominate at large radii (case II), the
iteration procedure was similar, however, the initial disk parameters
had to be estimated more carefully. This was done in two
steps. First, a disk model was constructed following the above
procedure. This model failed to produce a convincing
solution in the outer disk dominated parts (specially the surface brightness
profile) but allowed to estimate the
bulge and disk profile in the inner parts, where the bulge still
dominates. The bulge profile was then fitted by an r1/4 model and
extrapolated out to radii where the disk dominates. The such constructed
bulge model was subtracted from the galaxy and the remaining disk
was used as input disk for a further iteration.
In this way, a
satisfactory decomposition was achieved.
Figure 1 illustrates this procedure for NGC 4564.
In Fig. 1a we show the surface brightness
profile (uppermost panel) and the a4 and ellipticity profiles (middle and
lower panel) before
(filled circles) and after (crosses) subtraction of a first (too small)
disk
model. Although the subtraction of this disk model yields a bulge with
vanishing a4/a, the brightness profile of the bulge still shows
signatures of the disk: mainly a hump at radii > 23 arcsec (2.5 in
the a1/4 scale) and ellipticity values which continue increasing
at large radii. After having modified the bulge profile
and having constructed and
subtracted an r1/4 bulge model, a second input disk was obtained. With the
latter, a better solution (shown in Fig. 1b) was achieved. The change
in the ellipticity profile is noticeable (lower panel in Fig. 1b):
the bulge has lower ellipticity when compared with the previous solution.
![\begin{figure}
\centering
\includegraphics[width=8.5cm,clip]{fig1.ps}\end{figure}](/articles/aas/full/1998/14/ds7366/Timg15.gif) |
Figure 1:
Surface brightness, a4/a*100 and ellipticity profiles
of NGC 4564 a) before (filled circles)
and after (crosses) the subtraction of a too small disk and b)
before and after
subtraction of a brighter and larger disk (see text) |
As already mentioned in Sect. 3, a detailed decomposition of these
systems
is not possible by means of the present method. However, the
bar hypothesis infered from the behaviour of the
Fourier coefficients can be tested after subtraction of a bulge
model and examination of the residual structures. We follow here
the same procedure applied in Scorza & Bender (1995) to recover the embedded bar
in NGC 4660. As a first step, the decomposition method described above was
applied. This yielded an approximated bulge profile from which a bulge model
having constant position angle and ellipticity was constructed. This bulge
model was then subtracted from the galaxy image and the residual structures
were analysed. Notice that
in this case it is assumed that the observed twists and abrupt ellipticity
changes are due to the embedded bar component and therefore the
constructed bulge-model is free from these features.
Although triaxiality can also lead to projected twists of the isophotes
(see e.g. Benacchio & Galleta 1980) the bar hypothesis is more
likely for isotropic oblate rotators, which is the case of the galaxies
examined here.
In all galaxies showing the typical behaviour of
the Fourier coefficients described in Sect. 3 (case III),
elongated barred-like structures could be recovered after the bulge-model
subtraction. Examples are shown in Sect. 5.2.3.
Similar to Scorza & Bender (1995), the zero point calibration
was done here by comparing integrated fluxes within apertures with
values given in the literature (Poulain 1993). After calibration, we
derived characteristic parameters from growth-curve-fitting:
the half light radius  , the surface brightness
, the surface brightness  at
at  and the total apparent magnitude
and the total apparent magnitude  .All these parameters were derived for galaxies, bulges and disks separately.
For the latter, both
.All these parameters were derived for galaxies, bulges and disks separately.
For the latter, both  and
and  were
corrected to face-on.
were
corrected to face-on.
Because the disks analysed here often have surface brightness profiles
which deviate from exponentials and
central surface brightnesses are
ill-defined (see Scorza & Bender 1995), the best way to characterize
the disks is then by their mean effective surface brightness
 :
:
| 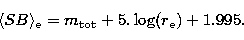 |
(2) |
However, given that throughout the literature the disks of late-type
galaxies are parameterized by
the extrapolated central surface brightness SB0 and scale
length  , we have determined also for comparison purposes the
SB0 for the
disks and a mean
, we have determined also for comparison purposes the
SB0 for the
disks and a mean
 value obtained from the fit of exponential growth curves to the
disks (for details see Scorza & Bender 1995).
In this case, the mean
value obtained from the fit of exponential growth curves to the
disks (for details see Scorza & Bender 1995).
In this case, the mean  is representative of the dominant exponential part of the disk profiles.
The SB0 values were obtained directly from the central intensities of
the disk models and corrected to face-on. Due to systematic
effects, assumptions concerning bulge
shapes, non-exponentiality of the disks and seeing, the errors for these
parameters could not be estimated reliably for each case. In general, however,
from exploring a range of models we have estimated the following rough errors:
is representative of the dominant exponential part of the disk profiles.
The SB0 values were obtained directly from the central intensities of
the disk models and corrected to face-on. Due to systematic
effects, assumptions concerning bulge
shapes, non-exponentiality of the disks and seeing, the errors for these
parameters could not be estimated reliably for each case. In general, however,
from exploring a range of models we have estimated the following rough errors:

 0.2 and
0.2 and 
 20% to 30%.
20% to 30%.
The distances to the galaxies were determined from the radial velocities
given in the literature (RC3 catalogue) and a Hubble constant of
H0=75 km s-1 Mpc-1). With these quantities, the absolute magnitudes and scale
lengths of the disks in kpc were derived. The absolute magnitudes
and the  were corrected for dust absorption
in the galactic plane according to Burstein (1984). The magnitudes and surface
brightness of the galaxy images
obtained only in the R band were transformed to the V band following
Peletier (1989):
were corrected for dust absorption
in the galactic plane according to Burstein (1984). The magnitudes and surface
brightness of the galaxy images
obtained only in the R band were transformed to the V band following
Peletier (1989):
| 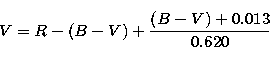 |
(3) |
where the (B-V) were taken from the RC3 catalogue.


Up: Stellar disks and embedded
Copyright The European Southern Observatory (ESO)
![]() :
:
![]() were corrected for dust absorption
in the galactic plane according to Burstein (1984). The magnitudes and surface
brightness of the galaxy images
obtained only in the R band were transformed to the V band following
Peletier (1989):
were corrected for dust absorption
in the galactic plane according to Burstein (1984). The magnitudes and surface
brightness of the galaxy images
obtained only in the R band were transformed to the V band following
Peletier (1989):