4 Radial-velocity curves and orbital parameters

  The radial-velocity monitoring of a binary star may lead to different qualitative results depending on the parameters of the orbital solution (period P, eccentricity e, amplitude K), the number of measurements or the observation sampling. The strategy for the presentation of the results will thus depend on these different cases. Situations possibly encountered are the following:

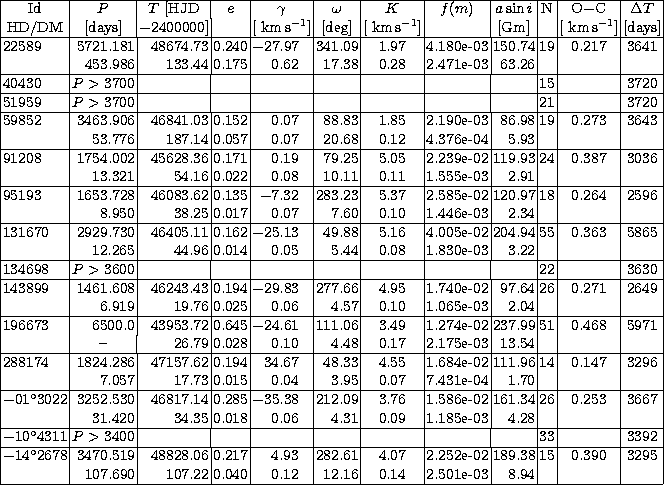
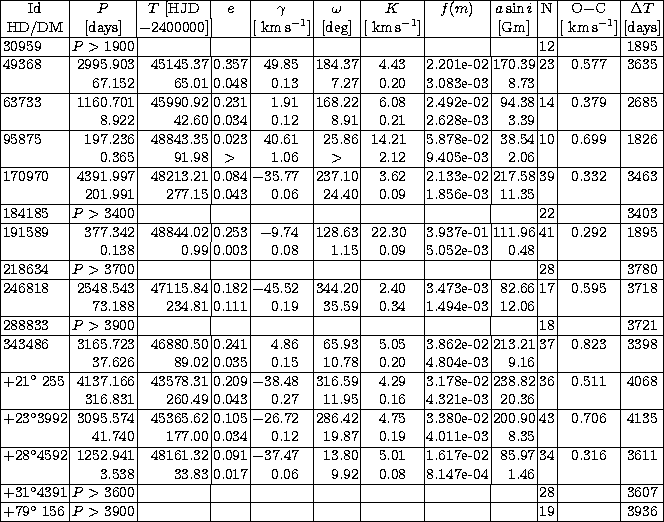
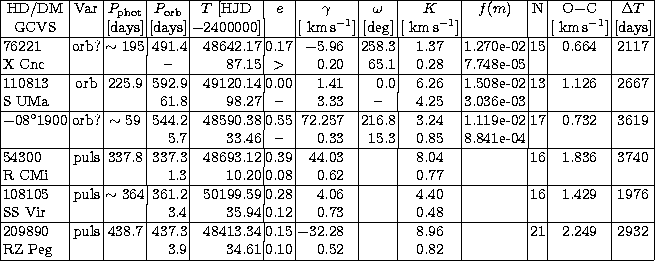
1) A stable solution is found and the orbital parameters can be derived (flag "o'' in Tables 2 and 3). This is the case for most of the orbits presented in this paper. A table is provided with the orbital parameters and their uncertainties and a few additional interesting related quantities as the number of measurements (N) used to derive the orbital solution or the residue (O-C) around this solution. The phase-folded orbital solution is then also displayed. Badly constrained parameters are readily identifiable by their large uncertainties.

2) The orbital solution exists but is not fully constrained. One or several parameters (usually P or e) have to be fixed (e.g. for an uncompletely-covered orbit or when the periastron passage in an eccentric orbit has been missed; flag "po'' in Tables 2 and 3). In such a case, the adequate orbital parameter is fixed to a probable value as given by the orbital solution with minimum residuals. The obtained minimized orbital elements are given in the same table as for case 1) but with no uncertainties on the fixed parameter(s). A diagram with the velocity measurements folded in phase is also provided.

3) The star has a clearly variable radial velocity but the period is insufficiently covered (usually just a drift is observed) to derive a preliminary orbit, even with fixed parameters (flag "mp'' in Tables 2 and 3). No solution is found. The minimum period ($P\gt P_{\rm min}$) is indicated in the table of orbital elements, along with the number of measurements and the time span of the observations. The figure only displays radial velocities as a function of Julian dates. In addition to the individual measurements available at the CDS (Sect. 3), the analysis paper (Jorissen et al. 1998) summarizes the interesting averaged quantities (radial velocity and corresponding uncertainty, etc.) for these stars.

4) No orbital solution can be found because of other sources of radial-velocity variations (jitter, flag "j'' in Table 3) masking a possible orbital motion. Average quantities are given in Jorissen et al. (1998).

In the following subsections the results for the various star samples described in Sect. 2 will be presented and discussed in turn.

  

Table 5: Orbital elements for strong barium stars. No uncertainties are given for fixed parameters. The symbol > is used for uncertainties exceeding the parameter values in case of badly constrained orbits. N is the number of measurements used to derive the orbital solution and O-C the residue around this solution. $\Delta T$ is the span of the observations

  

Table 6: Orbital elements for mild barium stars. No uncertainties are given for fixed parameters. N is the number of measurements used to derive the orbital solution and O-C the residue around this solution. $\Delta T$ is the span of the observations

  

Table 7: Orbital elements for the S stars with no (strong) light variations. The symbol > is used for uncertainties exceeding the parameter values in case of badly constrained orbits. N is the number of measurements used to derive the orbital solution and O-C the residue around this solution. $\Delta T$ is the span of the observations

  

Table 8: Orbital or pseudo-orbital (pulsational) elements for Mira S stars, SC stars and Tc-poor C stars. The most likely cause of the radial-velocity variations is given in Col. 2: "orb'' for orbital motion and "puls'' for intrinsic atmospheric phenomenon. No uncertainties are given for fixed parameters. The symbol > is used for uncertainties exceeding the parameter values in case of badly constrained orbits. N is the number of measurements used to derive the orbital solution and O-C the residue around this solution. $\Delta T$ is the span of the observations

4.1 Strong barium stars

Definitive or preliminary orbits have been obtained for all strong barium stars except HD 19014. The orbital parameters are given in Table 5. For two uncompletely-covered orbits ( HD 123949 and HD 211954), the periods have been fixed to minimized values (see item 2 above). In 8 cases, even though the Lucy-Sweeney test was compatible with a circular orbit at a 5% confidence level (Lucy& Sweeney 1971), the slightly "eccentric'' orbit has been listed, because in the case of barium stars, there is no physical argument to prefer the circular orbit (see Jorissen et al. 1998). The corresponding radial-velocity measurements folded in phase are displayed in Fig. 2.

BD $+38^\circ$118 is a triple hierarchical system. The long-period orbit (noted ab+c) describes the motion of the c component, relatively to the center of mass of the close (short-period) system (noted a+b). The orbits are obtained iteratively by correcting the short-period orbital motion from the long-period perturbation.

  

Figure 2: Phase-folded radial-velocity curves for the strong barium stars. Minimized periods (see item 2 in Sect. 4) were fixed for HD 123949 and HD 211954 because of the non-complete coverage of the orbits. BD$+38^\circ$118 is a triple hierarchical system

 

Figure 2: continued

4.2 Mild barium stars

Orbital elements were derived for 10 among the 14 mild barium stars presented in this section (Table 6), the others only allowing minimum period estimates. The corresponding phase-folded curves are displayed in Fig. 3, along with the temporal radial-velocity variations of the remaining 4 stars with no orbital solution.

The star HD 196673 deserves a special note. It belongs to the DAO sample with a spectroscopic orbit published by McClure & Woodsworth (1990). However, as shown by 2 new CORAVEL measurements, the inferred orbital period (P=4000d) was too short. Based on all the DAO+ CORAVEL measurements, we propose a new period (fixed to P=6500d), which is a lower bound to the actual period. The new preliminary orbital elements obtained by fixing the period to the above value are listed in Table 6.

  

Figure 3: Phase-folded radial-velocity curves for mild barium stars with orbital solutions. Open circles are for DAO measurements. Two new CORAVEL measurements allow us to propose a new minimum-period estimate for HD 196673. Long-period stars without orbital solutions have their radial velocities displayed as a function of Julian dates

 

Figure 3: continued

4.3 Photometrically non-variable S stars

Among the 16 binary S stars with no photometric variations presented in this subsection, an orbital solution has been derived for 10 of them whereas 6 have only minimum-period estimates. The results are given in Table 7. The corresponding phase diagrams are displayed in Fig. 4.

Note that BD $+21^\circ$255 is a visual binary, most probably of optical nature (Jorissen & Mayor 1992). Table 7 and Fig. 4 provide the orbit of the S star ( BD $+21^\circ$255 = PPM 91178 = SAO 75009 = HIC 8876), whereas the visual K-type companion ( BD $+21^\circ$255p = PPM 91177 = SAO 75008) is also a spectroscopic binary whose orbit is given in Jorissen & Mayor (1992).

The jitter level of the non-binary stars of the sample is of the order of 1-2 kms^-1 (Jorissen et al. 1998). Its hampering influence on the detection of binarity is thus limited to low-amplitude orbital motions.

  

Figure 4: Phase-folded radial-velocity curves of the photometrically non-variable S stars with orbital solutions. Long-period stars without orbital solutions have their radial velocities displayed as a function of Julian dates

 

Figure 4: continued