

Up: Einstein A-coefficients for rotational SiC, SiC SiC
In the circumstellar envelope of IRC +10216 a number of molecules in the
vibrationally excited state have been observed. Since the scientists are
optimistic to detect SiC2 in the vibrationally excited state at
177 cm-1 above the ground state, therefore Chandra & Sahu (1993)
calculated Einstein A-coefficients for rotational transitions in the
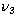 vibrationally excited state of SiC2. Their belief has a
strong support since a number of molecules observed in the vibrationally
excited state(s) in the envelope of IRC +10216 have the excited state(s) at
quite high energies above the ground state. However, for the detailed
study one has to account for both the ground and vibrationally excited
states for the same physical conditions in the atmosphere. Therefore,
Einstein A-coefficients for the rotational transitions in the ground
vibrational state are also needed. Besides 28SiC2, Einstein
A-coefficients for rotational transitions in the ground vibrational state
of 29SiC2 and 30SiC2 are also calculated.
vibrationally excited state of SiC2. Their belief has a
strong support since a number of molecules observed in the vibrationally
excited state(s) in the envelope of IRC +10216 have the excited state(s) at
quite high energies above the ground state. However, for the detailed
study one has to account for both the ground and vibrationally excited
states for the same physical conditions in the atmosphere. Therefore,
Einstein A-coefficients for the rotational transitions in the ground
vibrational state are also needed. Besides 28SiC2, Einstein
A-coefficients for rotational transitions in the ground vibrational state
of 29SiC2 and 30SiC2 are also calculated.
![\begin{figure}
\centering
\includegraphics [width=8cm]{1461f2.eps}\end{figure}](/articles/aas/full/1998/13/ds1461/Timg20.gif) |
Figure 2:
Energy level diagram if rotationl levels in the ground vibrational
state of 28SiC2 |
After the careful survey of the energy level diagram in the ground
vibrational state of 28SiC2 (Silicon Dicarbide) (Fig. 2), we predict
that the transition between the backbone
levels 202, 303, 404, 505  are of
specific interest.
Furthermore the ratios of the radiative lifetime of upper level to
that of the lower level for the transitions 3
are of
specific interest.
Furthermore the ratios of the radiative lifetime of upper level to
that of the lower level for the transitions 3 202,
404
202,
404
 303, 5
303, 5 404, 6
404, 6 505,
707
505,
707 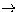 606, 808
606, 808 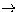 707, 909
707, 909 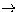 808 are 0.281, 0.415, 0.514, 0.586, 0.642, 0.683, 0.716,
respecively. This trend of increasing the value of the ratio of radiative lifetimes
with the quantum number J reflects the probability for the detection of transition
between the levels with higher values of J. However, the population of the levels
decreases with the increase of J.
Thus, in the ground vibrational state a compromising state may come
around the transition 606
808 are 0.281, 0.415, 0.514, 0.586, 0.642, 0.683, 0.716,
respecively. This trend of increasing the value of the ratio of radiative lifetimes
with the quantum number J reflects the probability for the detection of transition
between the levels with higher values of J. However, the population of the levels
decreases with the increase of J.
Thus, in the ground vibrational state a compromising state may come
around the transition 606 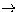 505. Hence, in the ground
vibrational state, the rotational
transition 606
505. Hence, in the ground
vibrational state, the rotational
transition 606 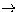 505 may play an important role
regarding the conclusions to be drawn about the excitation mechanism in
the envelope of IRC +10216. However, a detailed analysis of radiative
transfer for the three cases
505 may play an important role
regarding the conclusions to be drawn about the excitation mechanism in
the envelope of IRC +10216. However, a detailed analysis of radiative
transfer for the three cases
(i) For rotational transitions in the ground vibrational state.
(ii) For rotational transitions in the vibrationally excited 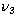 state.
state.
(iii) For the rotational and vib-rotational transitions in the ground
and vibrationally excited state
are to be carried out. In the further work, we intend to investigate the
radiative transfer calculations.
Acknowledgements
The work is financially supported by the Department of Science and
Technology, New Delhi through the project No. SP/S2/004/94 in which Ms.
Rashmi has joined as a Junior Research Fellow. Thanks are due to
Indira Gandhi National Open University, New
Delhi for providing necessary facilities. We are grateful to the learned
referee for making fruitful suggestions.


Up: Einstein A-coefficients for rotational SiC, SiC SiC
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\centering
\includegraphics [width=8cm]{1461f2.eps}\end{figure}](/articles/aas/full/1998/13/ds1461/Timg20.gif)
![]() state.
state.