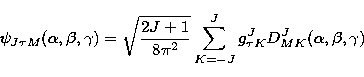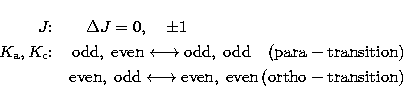Up: Einstein A-coefficients for rotational SiC, SiC SiC
High resolution spectroscopy has
shown that Silicon Dicarbide is a three membered ring molecule with
equivalent carbon atoms (Michalopoulos et al. 1984). Its linear isomer is
less stable than the ring structure
(Grev & Schaefer 1984). The bond
length of Si-C and C-C are 1.837 Å and 1.268 Å, respectively.
The geometry of Silicon Dicarbide molecule is shown in Fig. 1.
![\begin{figure}
\centering
\includegraphics [width=8cm,clip=]{fig1.eps}\end{figure}](/articles/aas/full/1998/13/ds1461/Timg4.gif) |
Figure 1:
The geometry of the 28SiC2 molecule |
The Silicon Dicarbide molecule is an a-type asymmetric top molecule
with dipole moment 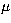 = 2.393 D (Suenram et al. 1989). SiC2 has
three fundamental vibrational modes
at
= 2.393 D (Suenram et al. 1989). SiC2 has
three fundamental vibrational modes
at 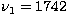 cm-1,
cm-1, 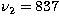 cm-1, and
cm-1, and
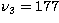 cm-1 (Shepherd & Graham 1985, 1988;
Gottlieb et al. 1989).
The wavefunction of an
asymmetric top molecule can be expressed as linear combination of wave
functions for a symmetric top molecule
(Chandra & Sahu 1993)
cm-1 (Shepherd & Graham 1985, 1988;
Gottlieb et al. 1989).
The wavefunction of an
asymmetric top molecule can be expressed as linear combination of wave
functions for a symmetric top molecule
(Chandra & Sahu 1993)
| 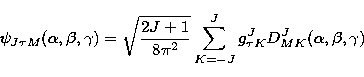 |
(1) |
where 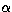 ,
, 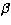 ,
, 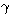 are the Eulerian angles specifying the
orientation of the molecule, J the rotational quantum number,
are the Eulerian angles specifying the
orientation of the molecule, J the rotational quantum number, 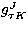 the expansion coefficient, DJM K the Wigner D-function.
the expansion coefficient, DJM K the Wigner D-function.
The rotational transitions are governed by the selection rules
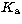 and
and 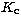 are sub-quantum
numbers and each of them can assume the values ranging from 0 to J.
On the basis of the selection rules, the rotational energy levels are
grouped into two sets of transitions behaving as if they belong to
two independent species. These species are referred to as para- and
ortho-species, respectively.
are sub-quantum
numbers and each of them can assume the values ranging from 0 to J.
On the basis of the selection rules, the rotational energy levels are
grouped into two sets of transitions behaving as if they belong to
two independent species. These species are referred to as para- and
ortho-species, respectively.
Table 1:
Molecular constants used in the calculations
|
|


Up: Einstein A-coefficients for rotational SiC, SiC SiC
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\centering
\includegraphics [width=8cm,clip=]{fig1.eps}\end{figure}](/articles/aas/full/1998/13/ds1461/Timg4.gif)