The data used in this paper come from the collection of the X-ray ![]() flares (Li & Zhang 1994), which collected all X-ray
flares (Li & Zhang 1994), which collected all X-ray ![]() flare
events listed in SGD (Solar Geophysical Data) in the time interval of 1 April 1987
to 30 December 1992
corresponding to the maximum period of the 22nd solar cycle.
The table gives the following parameters of each flare event:
date, beginning time, maximum time, ending time, X-ray class, and
position on the solar disk. The total number of the considered flare
events
is 2052. The sample does not
collect flare events before 1987 and after 1992,
because their number was not large
enough significant for a statistical analysis.
flare
events listed in SGD (Solar Geophysical Data) in the time interval of 1 April 1987
to 30 December 1992
corresponding to the maximum period of the 22nd solar cycle.
The table gives the following parameters of each flare event:
date, beginning time, maximum time, ending time, X-ray class, and
position on the solar disk. The total number of the considered flare
events
is 2052. The sample does not
collect flare events before 1987 and after 1992,
because their number was not large
enough significant for a statistical analysis.
So we just use the data listed in their table and do not add any data to
complete the analysis of an entire solar cycle.
Table 1 gives the number of the flares
classified by hemisphere and by X-ray class.

* The flare events are summed up into
the numbers of this row only from 1 April 1987. |
Here, S, N, E, and W stand for the southern, northern, eastern, and western hemispheres respectively; M and X stand for the X-ray flares of M and X classes (or importances) respectively; the last column gives the total number of the annual flare events, and the last row gives the total number in the flare-class within the considered six years.
The spatial distribution of flares in heliographic latitude is usually
studied
to determine whether there is a N-S spatial asymmetry or not, and whether
the
asymmetry is dependent on the intensities of the flares, or any other
associated
characteristics. Figure 1 gives the annual number ratio of the flare events
in the southern hemisphere (![]() = 1226) to those in the
northern hemisphere
(
= 1226) to those in the
northern hemisphere
(![]() = 826). There is no flare of X class occurring in 1987, here we let
the
value
= 826). There is no flare of X class occurring in 1987, here we let
the
value ![]() of this year equal to 1 for the flares of X class.
The same is
of this year equal to 1 for the flares of X class.
The same is ![]() in Fig. 3. Figure 1 clearly shows that the
flare
events
in the southern hemisphere are much more numerous than those
in the northern hemisphere
in five years of the six for M class, X class, and
in Fig. 3. Figure 1 clearly shows that the
flare
events
in the southern hemisphere are much more numerous than those
in the northern hemisphere
in five years of the six for M class, X class, and ![]() class
respectively. The ratio of the total number of the flare events
in the southern hemisphere to that in the northern hemisphere is 1.49 for
M class,
1.37 for X class,
1.48 for
class
respectively. The ratio of the total number of the flare events
in the southern hemisphere to that in the northern hemisphere is 1.49 for
M class,
1.37 for X class,
1.48 for ![]() class. An overall southern bias apparently prevailed
in the solar cycle 22.
The above numbers indicate that the flare events of
class. An overall southern bias apparently prevailed
in the solar cycle 22.
The above numbers indicate that the flare events of ![]() class in the southern hemisphere exceeded the events in the northern
hemisphere by an unexpected large percentage
class in the southern hemisphere exceeded the events in the northern
hemisphere by an unexpected large percentage ![]() during the
investigated
interval. This is a strong N-S asymmetry.
during the
investigated
interval. This is a strong N-S asymmetry.
 |
(1) |

 |
(2) |
These results are complimentary to several ones published recently. Oliver & Ballester (1994) and Atac & Ozguc (1996) stressed the dominance of southern hemisphere during most Solar Cycle 22 using sunspot areas and solar flare index, respectively. Such a result points out a possible trend in the behaviour of the N-S asymmetry.
If globally it is in good agreement with previous studies, we did not find
any variation with the flare class and any relation with the magnetic field
flux obtained by some of these studies.
Garcia (1990) found that the degree of N-S asymmetry apparently
is a function of the intensity of the studied events, and
the most intense events show the largest amount of N-S asymmetry. This statement
was valid for the solar Cycle 21 but according to our results it does not
seem to be confirmed for Solar Cycle 22.
Our statistical
results show that the degree
(![]() ) of N-S asymmetry for
the flares of X class is smaller than the degree (
) of N-S asymmetry for
the flares of X class is smaller than the degree (![]() ) for the
flares
of M class.
Howard (1974) ever studied solar magnetic flux
data
for the period 1967 to 1973. He found that the total flux in the
northern
hemisphere exceeded that in the southern hemisphere, but only by a small
percentage 7%. The discrepancy between our results and the Heras's results
could be due to the fact that
in the upper latitude the N-S asymmetry flux is less pronounced than in the
lower ones or
more difficult to establish because of the
weak statistics.
) for the
flares
of M class.
Howard (1974) ever studied solar magnetic flux
data
for the period 1967 to 1973. He found that the total flux in the
northern
hemisphere exceeded that in the southern hemisphere, but only by a small
percentage 7%. The discrepancy between our results and the Heras's results
could be due to the fact that
in the upper latitude the N-S asymmetry flux is less pronounced than in the
lower ones or
more difficult to establish because of the
weak statistics.
Further investigation of the relation between degree of
N-S asymmetry and intensity of studied events is needed in future.
Heliographic latitude of each flare event is plotted in Fig. 2 with
respect to the date of occurrence. Southern heliographic latitudes take
the negative sign in the figure. Several features and peculiarities are
immediately apparent. At the beginning of the 22nd solar cycle, the X-ray
![]() flares occurred in the relatively high latitudes (above
flares occurred in the relatively high latitudes (above
![]() ),
then, as the cycle is progressing, there was an obvious shift in the
statistical
centroïd position to the lower latitudes. The majority of the flare
events
occurred in the latitudes between
),
then, as the cycle is progressing, there was an obvious shift in the
statistical
centroïd position to the lower latitudes. The majority of the flare
events
occurred in the latitudes between ![]() and
and ![]() . Only 2 flares occurred in the
latitudes over
. Only 2 flares occurred in the
latitudes over ![]() , and no flares occurred in the latitudes over
, and no flares occurred in the latitudes over
![]() . Garcia (1990) gave the
distribution of
. Garcia (1990) gave the
distribution of ![]() flares
from 1969 to 1984 with respect to the heliographic latitude in Figs.
2
and 3 of his paper and find similar results.
The distribution in latitude of the flares is comparable to the sunspot
distribution.
flares
from 1969 to 1984 with respect to the heliographic latitude in Figs.
2
and 3 of his paper and find similar results.
The distribution in latitude of the flares is comparable to the sunspot
distribution.
The
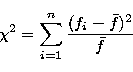 |
(3) |
|
|
Copyright The European Southern Observatory (ESO)