

Up: The thicknesses and inclinations
Subsections
Figures 1 and 2 present the correlations between the
flatness (H/D0) and thickness (H) and galaxy color
( ). The integrated colors of disk galaxies are
predominantly influenced by their star formation history (Searle et al.
1973), and the strong correlations observed
between color and flatness or thickness point to a coupling
between the flatness or thickness and the integrated
star formation history of galaxies.
). The integrated colors of disk galaxies are
predominantly influenced by their star formation history (Searle et al.
1973), and the strong correlations observed
between color and flatness or thickness point to a coupling
between the flatness or thickness and the integrated
star formation history of galaxies.
Figure 3 plots flatness
as a function of the corrected U-B color (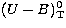 ), which
are taken from RC3,
the total U-B color index corrected for differential
galactic and internal extinction (to "face-on'') and for redshift.
The dependence of thickness on
), which
are taken from RC3,
the total U-B color index corrected for differential
galactic and internal extinction (to "face-on'') and for redshift.
The dependence of thickness on 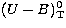 is illustrated in
Fig. 4.
is illustrated in
Fig. 4.
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig1.eps}
\vspace{2mm}\vspace{3mm}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg21.gif) |
Figure 1:
Flatness of spiral galaxy plotted versus the corrected B-V color |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig2.eps}
\vspace{2mm}\vspace{3mm}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg22.gif) |
Figure 2:
Thickness of spiral galaxy plotted versus the corrected B-V color |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig3.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg23.gif) |
Figure 3:
Flatness of spiral galaxy plotted versus the corrected U-B color |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig4.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg24.gif) |
Figure 4:
Thickness of spiral galaxy plotted versus the corrected U-B color |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig5.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg25.gif) |
Figure 5:
Flatness of spiral galaxy plotted versus the Hubble sequence |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig6.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg26.gif) |
Figure 6:
Thickness of spiral galaxy plotted versus the the Hubble sequence |
The tightness of the spiral pattern, in addition to the disk resolution
and bulge-to-disk ratio, are the fundamental criteria in Hubble's
(1926) classification of spirals.
It is interesting to see the dependence of flatness
on the Hubble type, which is shown in Fig. 5. The flatness of
a spiral galaxy decreases smoothly an average along the Hubble
sequence, but the dispersion in flatness among galaxies of the
same Hubble type is very large. Figure 6 shows the correlation
between thickness and the Hubble sequence.
Kennicutt & Kent (1983) presented the combined results of
photometric and spectrophotometric surveys of H emission
for 200 field and Virgo cluster galaxies. Romanishin
(1990) published large aperture photometric measurement of
emission
for 200 field and Virgo cluster galaxies. Romanishin
(1990) published large aperture photometric measurement of
![$\rm
{H}_{\alpha}+[\rm {NII}]$](/articles/aas/full/1998/12/ds7136/img27.gif) emission line strengths of 110 spiral galaxies.
We have measured the thicknesses of some spirals observed by them.
The results are listed in Table 3. We use the formula (Romanishin
1990):
emission line strengths of 110 spiral galaxies.
We have measured the thicknesses of some spirals observed by them.
The results are listed in Table 3. We use the formula (Romanishin
1990):
EW (Romanishin's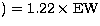 (KK's)
(KK's)
Table 3:
![$\rm
{H}_{\alpha}+[\rm {NII}]$](/articles/aas/full/1998/12/ds7136/img27.gif) equivalent width and thickness
equivalent width and thickness
|
|
Figure 7 shows the correlation of ![$\rm
{H}_{\alpha}+[\rm {NII}]$](/articles/aas/full/1998/12/ds7136/img27.gif) equivalent width with the thickness. There might be a negative correlation
between star formation activity and thickness of a galaxy, but the scatter
is large and there are only 20 samples. The thicknesses of NGC 628 and NGC 5194 are from Peng's paper (Peng 1988).
equivalent width with the thickness. There might be a negative correlation
between star formation activity and thickness of a galaxy, but the scatter
is large and there are only 20 samples. The thicknesses of NGC 628 and NGC 5194 are from Peng's paper (Peng 1988).
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig7.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg31.gif) |
Figure 7:
![$\rm
{H}_{\alpha}+[\rm {NII}]$](/articles/aas/full/1998/12/ds7136/img27.gif) emission line plotted versus the thickness emission line plotted versus the thickness |
![\begin{figure}
\centering
\includegraphics[height=8.5cm,angle=-90]{DS7136.fig8.eps}\end{figure}](/articles/aas/full/1998/12/ds7136/Timg32.gif) |
Figure 8:
Thickness of spiral galaxy plotted versus the Neutral hydrogen masses |
Figure 8 plots the relation between thickness and neutral hydrogen
masses. The neutral hydrogen mass is derived by de Vaucouleurs et al. (1991,
RC3),
| 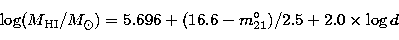 |
(5) |
where 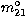 , from RC3, is the 21-cm emission line magnitude and
corrected for self-absorption and d, in Mpc, is the distance of a galaxy.
, from RC3, is the 21-cm emission line magnitude and
corrected for self-absorption and d, in Mpc, is the distance of a galaxy.
Figure 8 suggests that a thicker galaxy contains
more neutral hydrogen, although the dispersion is large.
Acknowledgements
We would like to thank Prof. Jiehao Huang for his help in finishing
this paper. We also thank Prof. Jingyao Hu for his hospitality
and discussion at the Xinglong Observational Station of Beijing Observatory,
and are grateful to Rui Chen, Zhaohui Ji and Zhaohui Shang for their help.
We wish to thank Prof. Zongyun Li for a valuable discussion.
This work is supported by the National Nature Science
Foundation, the National Grand Project "Climbing Up" of China and the
Doctoral Program Foundation of State Education Commission of China.


Up: The thicknesses and inclinations
Copyright The European Southern Observatory (ESO)
![]() ), which
are taken from RC3,
the total U-B color index corrected for differential
galactic and internal extinction (to "face-on'') and for redshift.
The dependence of thickness on
), which
are taken from RC3,
the total U-B color index corrected for differential
galactic and internal extinction (to "face-on'') and for redshift.
The dependence of thickness on ![]() is illustrated in
Fig. 4.
is illustrated in
Fig. 4.
![]() (KK's)
(KK's)