A diagram representing the excess in line
ratios for [OI] and other transitions is illustrated in Fig. 3
(see the trend designated "OBSERVED"), wherein we indicate a parameter
R(GEN) = ![]() for the general population of sources; where
for the general population of sources; where ![]() represents the mean logarithmic line ratio for the radiative
models combined,
represents the mean logarithmic line ratio for the radiative
models combined, ![]() is the corresponding
parameter for the observed nebular sample, and bipolar nebulae have been
excluded (see the further discussion in Sect. 4.1). We have also corrected
R([OIII]) for use of inappropriately low model central star temperatures, as
discussed in Sect. 4. Broadly speaking, therefore, R(GEN) is an indication
of the proportionate excess in line ratios over those anticipated through
radiative modelling.
is the corresponding
parameter for the observed nebular sample, and bipolar nebulae have been
excluded (see the further discussion in Sect. 4.1). We have also corrected
R([OIII]) for use of inappropriately low model central star temperatures, as
discussed in Sect. 4. Broadly speaking, therefore, R(GEN) is an indication
of the proportionate excess in line ratios over those anticipated through
radiative modelling.
![\begin{figure}
\includegraphics[]{1473f3.eps} \end{figure}](/articles/aas/full/1998/12/ds1473/Timg28.gif) |
Figure 3: Observed variation of R(GEN) as a function of transition, together with comparative predictions for selected planar shock models |
It is apparent that excesses in [OI] represent by far the most
serious departures from modelling of any of the transitions considered
here. This, in part, is likely to be the result of low [OI] model line
ratios, such that small excesses in all lines would lead to
disproportionately large effects in this particular transition. Indeed, the
evaluation of a median excess parameter ![]() suggests that the trends
illustrated in Fig. 3 are consistent with a similar excess in all
transitions - a species of "veiling" over and above that arising through
normal radiative excitation. How could such a component arise?
suggests that the trends
illustrated in Fig. 3 are consistent with a similar excess in all
transitions - a species of "veiling" over and above that arising through
normal radiative excitation. How could such a component arise?
One possible indication is afforded through the work Reay et al.
(1988) and Phillips et al. (1992), where it is noted
that [OI] line intensities are proportional to the intensity of shocked
![]() m H2 S(1) emission. One plausible explanation,
therefore, is that we are witnessing a small shock excess at the HI/HII
interface of optically thick sources, or over the surfaces of neutral
condensations within the primary ionised mass.
m H2 S(1) emission. One plausible explanation,
therefore, is that we are witnessing a small shock excess at the HI/HII
interface of optically thick sources, or over the surfaces of neutral
condensations within the primary ionised mass.
Under these circumstances, and given that ![]() , and
, and ![]() , then
, then ![]() may be equated with
may be equated with ![]() ; where
; where ![]() is the H
is the H![]() emission intensity,
emission intensity,
![]() is the intensity of the transition under investigation, and
superscripts R and S refer respectively to the radiative and shock terms.
Where
is the intensity of the transition under investigation, and
superscripts R and S refer respectively to the radiative and shock terms.
Where ![]() and
and ![]() then
then ![]() . In other words,
. In other words, ![]() for [OI]
will be broadly proportional to the shocked line intensity. Note, in this
respect, that force-fitting of observed [OI] line ratios to a mix of shock
and radiative modelling would imply values
for [OI]
will be broadly proportional to the shocked line intensity. Note, in this
respect, that force-fitting of observed [OI] line ratios to a mix of shock
and radiative modelling would imply values ![]() for shock velocities
for shock velocities ![]() km s-1; a ratio which
decreases still further as
km s-1; a ratio which
decreases still further as ![]() increases.
increases.
Inspection of the shock
results of Raymond et al. (1988) and Hartigan et al.
(1987) reveals that a variety of specifications might satisfy
required excess characteristics, including models I20![]() I80,
A100, D100 and bow shock models 3 and 4. These are characterised by fairly
modest velocities
I80,
A100, D100 and bow shock models 3 and 4. These are characterised by fairly
modest velocities ![]() km s-1; comparable
to [OIII]/HI expansion velocities
km s-1; comparable
to [OIII]/HI expansion velocities ![]() km s-1 in
normal PN (e.g. Phillips 1989; although note that [OII]/[NII]
velocities (characteristic of the nebular peripheries) are typically
km s-1 in
normal PN (e.g. Phillips 1989; although note that [OII]/[NII]
velocities (characteristic of the nebular peripheries) are typically ![]() larger).
larger).
Although the excess trends,
observed expansion velocities and shock modelling appear therefore to offer
a consistent scenario, care must be taken in the interpretation of such
results; in particular, the synthetic data used to assess ![]() are far from representing an appropriate balance of models.
Thus, although the radiative modelling appears to simulate observed trends
tolerably well (see later), slight errors in
are far from representing an appropriate balance of models.
Thus, although the radiative modelling appears to simulate observed trends
tolerably well (see later), slight errors in ![]() would have a disproportionate effect upon
would have a disproportionate effect upon ![]() in all excepting the [OI] results.
in all excepting the [OI] results.
A more interesting question, under these circumstances, is whether the very much more greatly enhanced [OI] line ratios are consistent with plausible shock modelling. To investigate this, we note that for a shock extending uniformly over the surface of a spherical nebula
![\begin{displaymath}
\frac{^{\rm s}I({\rm OI})}{^{\rm R}I({\rm H}\beta )}=\frac{7...
...rgs~cm^{-2}s^{-1}}}\right]}{n^2_{\rm e}(R/{\rm pc})\varepsilon}\end{displaymath}](/articles/aas/full/1998/12/ds1473/img48.gif)
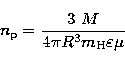
![\begin{displaymath}
\frac{^{\rm s}I({\rm OI})}{^{\rm R}I({\rm H}\beta )}=\frac{3...
...}I({\rm OI})/^{\rm s}I({\rm H}\beta )] [R/{\rm pc}]^2 U}{M/M_0}\end{displaymath}](/articles/aas/full/1998/12/ds1473/img55.gif)
In contrast, the trend towards smaller values of ![]() with
decreasing R (e.g. Phillips 1989) might be expected to work
in the reverse direction, and lead to corresponding decreases in [OI]
shock excesses; a factor which may be responsible for the shallow secular
variations in [OI]/H
with
decreasing R (e.g. Phillips 1989) might be expected to work
in the reverse direction, and lead to corresponding decreases in [OI]
shock excesses; a factor which may be responsible for the shallow secular
variations in [OI]/H![]() noted in Sect. 3.2.
noted in Sect. 3.2.
Finally, the theoretical
trends for a range of transitions and velocities are presented in
Fig. 3. It can be seen that shock modelling predictions are more
than adequate, and accommodate a good proportion of the excess in [SII]
which, on this basis, would appear to be shock enhanced by a factor ![]() . Such a result may have severe consequences for our understanding of
nebular densities, since it is apparent that [SII] line ratios would be to
some degree representative of compressed post-shock regimes, and imply
higher densities than are appropriate for the primary nebular shells.
. Such a result may have severe consequences for our understanding of
nebular densities, since it is apparent that [SII] line ratios would be to
some degree representative of compressed post-shock regimes, and imply
higher densities than are appropriate for the primary nebular shells.
A further possible source for such trends may arise through UV shadowing, appreciable ionisation stratification, and charge exchange reactions in zones of partial ionisation. Such mechanisms may not, in fact, be entirely divorced from the process of shock excitation considered above, since Rayleigh-Taylor and Kelvin-Helmholtz instabilities would be expected to lead to frontal irregularities, and the possible development of globular neutral condensations within the primary ionised zones (cf. Capriotti 1973). Whether such features could account for the "veiling" excesses noted above is, however, far from clear, and requires further analysis.
Finally, we have noted that low-excitation emission appears often to be
associated with small-scale condensations and filamentary structures (see
for instance the spectro-morphological studies of Phillips & Reay
(1980) and Boeshaar (1974), high resolution imaging of
nearby nebulae (e.g. NGC 7293, NGC 6543; e.g. Harrington
1995; O'Dell & Handron 1996), and the line modelling
analyses of Hyung et al. (1994, 1995), Köppen
(1979), Boeshaar (1974) and Hyung & Aller
(1995). It is therefore pertinent to ask whether the strength of the
[OI] transition may be related to the degree of fragmentation of the
primary shell. More specifically, is there a correlation between [OI] line
strengths and the nebular filling factor ![]() ? To investigate this
question, we have plotted the variation of I([OI]) against values of
? To investigate this
question, we have plotted the variation of I([OI]) against values of
![]() derived from Boffi & Stanghellini (1994),
Kingsburgh & Barlow (1992), Kingsburgh & English
(1992) and Mallik & Peimbert (1988) (Fig. 4;
where we have adopted averaged values of
derived from Boffi & Stanghellini (1994),
Kingsburgh & Barlow (1992), Kingsburgh & English
(1992) and Mallik & Peimbert (1988) (Fig. 4;
where we have adopted averaged values of ![]() where multiple
estimates are available). Cursory inspection suggests that there is little
correlation between the parameters. Whilst [OI] excitation may be
associated with nebular condensations, therefore, it would appear that
such emission is only superficially related to primary shell
fragmentation.
where multiple
estimates are available). Cursory inspection suggests that there is little
correlation between the parameters. Whilst [OI] excitation may be
associated with nebular condensations, therefore, it would appear that
such emission is only superficially related to primary shell
fragmentation.
Given that many of these line intensities increase with increasing source
radius (see Sect. 4 below), the trends also correspond to an evolutionary
sequence in which younger nebulae (high densities, lower central star
temperatures) are located to the lower left of Figs. 1, and older
nebulae are to the upper right.
3) Comparison between theoretical and model
results for [NI], [OI], [OII], and [SII] reveals that the levels of scatter
are comparable. Much of the theoretical scatter derives from the range of
parameters ![]() ,
, ![]() , and Z employed for the radiative
modelling, as well as through the contributions of differing lines-of- sight
through the nebular shells. This, in turn, underlines the necessity of
employing multiple line-of-sight analyses for any radiative investigation of
nebular line strengths; a factor not always appreciated in previous
analyses.
, and Z employed for the radiative
modelling, as well as through the contributions of differing lines-of- sight
through the nebular shells. This, in turn, underlines the necessity of
employing multiple line-of-sight analyses for any radiative investigation of
nebular line strengths; a factor not always appreciated in previous
analyses.
Note that the size of scatter exceeds probable errors (Sect. 2) by a factor
![]() .
.
4) Although correlation coefficients are relatively low, there appears to be
evidence for statistically significant variations in [OI], [SII], and [NI] line
intensity with nebular radius (Fig. 2). This does not apply for
higher excitation transitions such as [SIII], HeII, [OIII] and He I. The
radial gradient for [NI] appears significantly greater than for any other
ion, whilst gradients for [OI] and [SII] are comparable.
Such trends would be at variance with radiative modelling of ionisation-bound
nebulae, given likely evolutionary trends in T* and ![]() . On the
other hand, careful perusal of these figures suggests that much of the
apparent variation may arise from a jump in low-excitation line-strengths
close to R = 0.1 pc, by typical factors of between 0.5 and 0.75 dex;
that is, as a result of the transition from radiatively-bound to
density-bound ionisation structures.
. On the
other hand, careful perusal of these figures suggests that much of the
apparent variation may arise from a jump in low-excitation line-strengths
close to R = 0.1 pc, by typical factors of between 0.5 and 0.75 dex;
that is, as a result of the transition from radiatively-bound to
density-bound ionisation structures.
5) [SIII] intensities were not modelled by Gruenwald & Viegas
(1992), although they appear to be broadly comparable to those
expected through shocks (Fig. 1i).
6) The variation of HeI with HeII differs from most other trends in
revealing a relatively constant ratio I(HeI)/I(H![]() ) up to the limiting
value log(102 I(HeII)/I(H
) up to the limiting
value log(102 I(HeII)/I(H![]() ))
)) ![]() , after which there is some
down-turn in ratios. Such trends are broadly consistent with radiative
analyses, as noted from the model results illustrated in Fig. 1b;
where we have assumed model nebulae to be optically thick, spherical and
homogeneous, with typical densities
, after which there is some
down-turn in ratios. Such trends are broadly consistent with radiative
analyses, as noted from the model results illustrated in Fig. 1b;
where we have assumed model nebulae to be optically thick, spherical and
homogeneous, with typical densities ![]() , and electron
temperatures
, and electron
temperatures ![]() K (the relevant emission parameters are
insensitive to these parameters). We have also assumed n(He)/n(H) =
0.115, case B conditions, a range of stellar temperatures 3 104 K
K (the relevant emission parameters are
insensitive to these parameters). We have also assumed n(He)/n(H) =
0.115, case B conditions, a range of stellar temperatures 3 104 K ![]() K, and adopted a blackbody approximation to the stellar
continuum. Ratios refer to lines of sight through the nebular cores.
K, and adopted a blackbody approximation to the stellar
continuum. Ratios refer to lines of sight through the nebular cores.
The downturn in I(HeI)/I(H![]() ) for large values of
I(HeII)/I(H
) for large values of
I(HeII)/I(H![]() ) occurs for high central star temperatures, and
applies (in particular) to density-bound structures.
) occurs for high central star temperatures, and
applies (in particular) to density-bound structures.
Finally, note that the
similarity of HeI and H![]() emission regimes for large ranges of central
star temperature, and the relative insensitivity of emission coefficients
to
emission regimes for large ranges of central
star temperature, and the relative insensitivity of emission coefficients
to ![]() and
and ![]() would lead to comparable HeI line ratios
irrespective of the mode of spectral sampling. This, in large part, is
probably responsible for the reduced scatter in HeI compared to [SII] and
other intermediate excitation transitions.
would lead to comparable HeI line ratios
irrespective of the mode of spectral sampling. This, in large part, is
probably responsible for the reduced scatter in HeI compared to [SII] and
other intermediate excitation transitions.
7) The low scatter, invariant
trend of [OIII] line ratios (Figs. 1c, e) is also broadly
consistent with the distribution expected for radiative line excitation.
For very much the same reasons as were cited for HeI above, [OIII]/H![]() ratios are expected to be reasonably consistent over a broad range of
central star temperatures, and as a function of projected shell location.
ratios are expected to be reasonably consistent over a broad range of
central star temperatures, and as a function of projected shell location.
The failure of the radiative modelling to reproduce these trends appears to
arise, in part, from a sensitivity in [OIII]/H![]() ratios to low central
star and nebular temperatures; both sets of parameters are smaller (in
certain models) than would be appropriate for the spectral data base
investigated here.
ratios to low central
star and nebular temperatures; both sets of parameters are smaller (in
certain models) than would be appropriate for the spectral data base
investigated here.
Copyright The European Southern Observatory (ESO)