5 Line widths and $\log V_{\rm m}$

Line widths are measured on the observed profile at two standard levels corresponding to 20% and 50% of the maximum intensity of the line. The results listed in Table 7 (Cols. 7 and 9) have been corrected to the optical velocity scale. According to Fouqué et al. (1990), the mean measurement error is equal to $3 \cdot \sigma(V_{20})$ and $2 \cdot \sigma(V_{20})$for the 20% and 50% widths, respectively. We give in column 11 the derived value of the logarithm of the maximum of circular velocity $\log V_{\rm m}$.It has been calculated as follows. The widths W₂₀ and W₅₀ are first corrected for resolution effect:

$$W_{l,R=0} = W_{l,R} +(0.014 \cdot l - 0.83)$$

for l= 20 and l=50 (Bottinelli et al. 1990), and further corrected for internal velocity dispersion:

$$W_{\rm c} = W^2 + w_{\rm t}^2(1-2{\rm e}^{-W_{\rm s}^2/w_{\r... ...^2}) - 2W\cdot w_{\rm t}(1-{\rm e}^{-W_{\rm s}^2/w_{\rm r}^2})$$

where $w_{\rm t} = 2\sigma_{\rm z}\cdot k(l)$, assuming an isotropic distribution of the non-circular motions $\sigma_{\rm z}$ = 12 km s^-1 and a nearly gaussian velocity distribution (k(20)=1.96 and k(50)=1.13; Fouqué et al.1990).

Corrected W₂₀ and W₅₀ are finally used to calculate $\log V_{\rm m}$:

$$\log V_{\rm m} = (2\log{W_{20}}+\log{W_{50}})/3 - \log{(2\sin{incl})}.$$

Where the inclination incl is derived from:

$$\sin^2(incl)= \frac{1-10^{2\log R_{25}}}{1-10^{2\log r_0}}$$

R₂₅ is the axis ratio and $\log r_0$= 0.43 + 0.053T for type T= 1 to 7 and $\log r_0$=0.38 for T=8. The actual uncertainty on $\log V_{\rm m}$ has been calculated according to Bottinelli et al. 1983. 94% of our observations have a signal to noise ratio S/N greater than 3; 62% have a signal to noise ratio greater than 5. Figure 3 shows the observed line widths as a function of S/N.

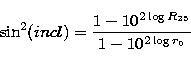
For information, the above corrections for resolution effect and non-circular motions represent on average about 18% and 11% of the observed line width, for the 20% and 50% level respectively. They lead to a correction of $\sim$3.3% on average on $\log V_{\rm m}$.

  

Figure 3: observed line width, a) $\rm W_{20}$ and b) $\rm W_{50}$, as a function of signal to noise ratio S/N