6 Analysis

6.1 Possible biases in the sample

Statistical analyses of this sample have to take into account and, if necessary, to correct for possible biases induced by the fact that some stars are misclassified as galaxies in the photometric catalogue, not all spectra have produced a measurable redshift and not all objects have been observed.

We have verified that the magnitude distribution of the stars is consistent with that of the total sample and therefore does not bias any analyses.

The small fraction ($\sim\! 5\%$) of objects with unmeasurable redshift has various origins: $\sim\! 13 \%$ of them correspond to undeblended pairs (see Sect. 2) for which the object coordinates fall in between the two components, while most cases are due to not well connected fibers or to observations with bad weather conditions. This kind of incompleteness is higher for fainter objects (see Fig. 2): note, however, that the maximum fraction of galaxies for which the spectra did not provide a useful z determination is $\sim\! 7\%$ for the faintest galaxies of our survey ($b_{\rm J}=19.4$).

We have verified that the magnitude distribution of not-observed objects ($\sim\! 10\%$) is consistent with being a random extraction from the total sample. The main bias for such objects is introduced by the impossibility of observing, in a given OPTOPUS exposure, two objects closer than $\sim$25 arcsec. Although the MEFOS observations and the repeated observations of the same fields have reduced somewhat this bias, it is still significantly present in the data. This is clearly seen in Fig. 3 which shows the observed distribution of nearest neighbour distances ($d_{\rm nn}$) for the entire photometric catalogue (4487 objects; solid histogram) and for the 444 objects which have not been observed spectroscopically (dashed histogram). The curves superimposed on the two histograms show the expected distributions of $d_{\rm nn}$ on the basis of the measured angular correlation function. The excess of not-observed objects which have a neighbour at a distance smaller than 50 arcsec is 132 $\pm$ 14 (183 objects in the data while 54 would be expected); some, less significant excess (35 $\pm$ 11) is present also for $d_{\rm nn}$ in the range 50-100 arcsec. Another way of characterizing the same bias is through the ratio between the not-observed objects and the total number of objects in the photometric catalogue as a function of $d_{\rm nn}$. This ratio is 0.31, 0.13 0.10, 0.06 for $d_{\rm nn} < 30$, $30 \le d_{\rm nn} < 50$, $50 \le d_{\rm nn} < 100$, $100 \le d_{\rm nn}$, respectively. Because of this bias, the spectroscopic catalogue can not be used in a straightforward way for studying, for example, the statistics of the number of close pairs or for analyzing the three dimensional correlation function on very small scales.

  

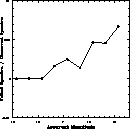Figure 2: Fraction of failed spectra over the total number of observed objects as a function of magnitude. Note that, even in the faintest bin, this fraction is always lower than $7\%$

  

Figure 3: Observed distribution of nearest neighbour distances ($d_{\rm nn}$) for the entire photometric catalogue (4487 objects; solid histogram) and for the 444 objects which have not been observed spectroscopically (dashed histogram). The curves superimposed on the two histograms show the expected distributions of $d_{\rm nn}$ on the basis of the measured angular correlation function

6.2 Statistical analysis of velocity errors

The errors on the velocities listed in Cols. (7) and (10) of Table 3 are the formal errors given by the IRAF tasks XCSAO and EMSAO for $v_{\rm abs}$ and $v_{\rm emiss}$, respectively. Their distributions are shown in Fig. 4: the median error is 64 km/s for $v_{\rm abs}$ and 31 km/s for $v_{\rm emiss}$.In order to have a better estimate of the true errors, we have analyzed the differences in the measured velocities ($\Delta v$) of the galaxies which have been observed more than once (156 galaxies with two measurements of $v_{\rm abs}$ and 64 galaxies with two measurements of $v_{\rm emiss}$). For both these samples the histograms of $\Delta v$ normalized to the formal errors are significantly larger than expected if these formal errors were correct estimates of the true errors. By fitting these distributions with Gaussian curves, the dispersions of the best fitting Gaussians are 1.53 and 2.10 for $v_{\rm abs}$ and $v_{\rm emiss}$, respectively. This implies that, assuming that the ratio between the true and the formal errors is a constant for all measurements, the true errors can be estimated by multiplying the errors given in Table 3 by these factors.

  

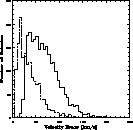Figure 4: Distribution of the errors on the measured velocity, for both $v_{\rm abs}$ (solid histogram) and $v_{\rm emiss}$ (dashed histogram)

The factor found for $v_{\rm abs}$ is in agreement with other values reported in the literature from similar analyses: for instance, Bardelli et al. (1994) found a factor 1.87 from a comparison of two sets of OPTOPUS observations (45 galaxies) reduced with different packages (IRAF and MIDAS) and by different authors; Malumuth et al. (1992), using multiple observations of 42 galaxies reduced in the same way, found a factor 1.6.

6.3 Systematic difference between $v_{\rm emiss}$ and $v_{\rm abs}$

For about 750 galaxies we could measure the redshift both from absorption and from emission lines. The distribution of the difference ($v_{\rm abs} - v_{\rm emiss}$) is well fitted by a Gaussian peaked at $\sim 100$ km/s. We have performed a number of tests, and we can exclude a zero-point error. Also in the Las Campanas redshift survey a similar systematic difference between the absorption and the emission velocities has been found, and the authors have chosen to correct for it by using a separate average template with large Balmer lines to fit emission line galaxies (Shectman et al. 1996). They suggest that the systematic effect is mainly due to the blend between $\rm H\epsilon$ and $\rm Ca H$ lines. On the other hand, we have decided to use in any case the best-fitting template, for sake of homogeneity in the redshift measures. A more general discussion about this point will be found in Cappi et al. (1998).