

Up: The DELTA photon counting
The data quantization on 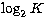 bits may cause
bits may cause  for a given photo-event. Misdirected projections due to
bad optical alignment, or small errors in the CCD spot ranging
may have the same effect. A tolerance
for a given photo-event. Misdirected projections due to
bad optical alignment, or small errors in the CCD spot ranging
may have the same effect. A tolerance
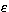 must be set, replacing Eq. (4) by the double inequality:
must be set, replacing Eq. (4) by the double inequality:
|  |
(6) |
This may cause the null-sum test to fail and create incorrect
photo-events. Suppose a photon having  -projections
(a1,b1,c1) which comply with the inequality:
-projections
(a1,b1,c1) which comply with the inequality:
|  |
(7) |
There may exist lists  ,
, 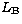 , and
, and  , such
that changing one
, such
that changing one  -coordinate among a1, b1, or
c1 by another one in the lists leaves Eq. (7) unchanged.
The same thing may happen by changing two
-coordinate among a1, b1, or
c1 by another one in the lists leaves Eq. (7) unchanged.
The same thing may happen by changing two  -coordinates
(either a1 and b1, or a1 and c1, or b1 and
c1). The back-projection process will therefore generate an
extra photon. As this pseudo-photon is a crossover between two
or three existing photons, we call it "cross-photon''.
There are two types of cross-photons. The first type regards
those made by crossover of two existing photons (two
-coordinates
(either a1 and b1, or a1 and c1, or b1 and
c1). The back-projection process will therefore generate an
extra photon. As this pseudo-photon is a crossover between two
or three existing photons, we call it "cross-photon''.
There are two types of cross-photons. The first type regards
those made by crossover of two existing photons (two
 -coordinates from the same existing photon). The second
type is a cross-photon having its
-coordinates from the same existing photon). The second
type is a cross-photon having its  -coordinates
originating from three different existing photons.
-coordinates
originating from three different existing photons.
Type-1 cross-photons are due to the non-zero tolerance
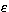 . Type-2 cross-photons occur with an increasing
probability when three or more photons are present in the same
frame.
. Type-2 cross-photons occur with an increasing
probability when three or more photons are present in the same
frame.
In order to assess the frequency of occurence of
cross-photons, one of us (SM) wrote a simulation software
generating projections from random numerical "photons''. The
number of generated photons per frame is variable and complies
with Poisson's law. Given
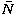 , the average number of photons per frame, this software
draws a variable number N of photons for each frame, such as:
, the average number of photons per frame, this software
draws a variable number N of photons for each frame, such as:
|  |
(8) |
We considered  and we set K=1024, as in the
prototype to be built (see Sect. 5). We measured the quantity
of type-1 and type-2 cross-photons generated, normalized by the
number of input photons. Figure 2 plots the results for
several values of
and we set K=1024, as in the
prototype to be built (see Sect. 5). We measured the quantity
of type-1 and type-2 cross-photons generated, normalized by the
number of input photons. Figure 2 plots the results for
several values of
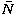 and
and 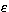 . It clearly appears that type-2
cross-photons dominate for large
. It clearly appears that type-2
cross-photons dominate for large 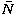 .
.
![\begin{figure}
\centering
\includegraphics [width=7cm]{fig2.eps}\end{figure}](/articles/aas/full/1998/11/ds1423/Timg35.gif) |
Figure 2:
Results of numerical simulations with a
"Poisson'' photon generator. Percentage (normalization by the
number of incoming photo-events) of type-1
(solid line) and type-2 (dashed line) cross-photons
generated, for different average numbers of photons per frame:
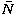 , and null-sum test tolerance in
pixels: , and null-sum test tolerance in
pixels: 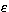 |


Up: The DELTA photon counting
Copyright The European Southern Observatory (ESO)
![]() bits may cause
bits may cause ![]() for a given photo-event. Misdirected projections due to
bad optical alignment, or small errors in the CCD spot ranging
may have the same effect. A tolerance
for a given photo-event. Misdirected projections due to
bad optical alignment, or small errors in the CCD spot ranging
may have the same effect. A tolerance
![]() must be set, replacing Eq. (4) by the double inequality:
must be set, replacing Eq. (4) by the double inequality:

![]() . Type-2 cross-photons occur with an increasing
probability when three or more photons are present in the same
frame.
. Type-2 cross-photons occur with an increasing
probability when three or more photons are present in the same
frame.
![]() , the average number of photons per frame, this software
draws a variable number N of photons for each frame, such as:
, the average number of photons per frame, this software
draws a variable number N of photons for each frame, such as:
