2 CCD observations and data reductions

The standard photometry presented here satisfies the needs for photographic photometry calibrations in two fields along the meridian section of the Milky Way toward the galactic anticenter; the North galactic pole (NGP) region is centered at ($l\simeq 162^\circ$, $b\simeq 87^\circ$), and the galactic plane region (GPR) at ($l\simeq 134^\circ$, $b\simeq -2^\circ$) around the open cluster STOCK 2. These fields are part of a systematic study (which includes a total of twelve regions) aiming at the detailed investigation of the structural and kinematical properties of the Galaxy (Spagna et al. 1996, and references therein). New CCD observations have been obtained to establish sequences of standard stars in the $BVR_{\rm c}$ Johnson-Cousins photometric system, down to $V \simeq$ 18.0 and 18.5, for GPR and NGP respectively.

$BVR_{\rm c}$ CCD data for the GPR and NGP fields were taken at Mt. Hopkins using the 1.2 m telescope equipped with a CCD camera (scale $\simeq 0\hbox{$.\!\!^{\prime\prime}$}67$/pixel), covering $11'\times 11'$.The GPR, that was observed on October 15 1993, is centered on star No. 49 from the list of Krzeminski & Serkowski (1967). The NGP fields, which were imaged the night of June 5 1994, are located respectively to the center (I), the North-East (II) and North-West (III) edges of the NGP region on the photographic plates we tackled. The center coordinates of all the fields are reported in Table 1.

  

Table 1: Celestial (J2000.0) and galactic coordinates of the CCD fields

The CCD frames were reduced utilizing standard packages; bias subtraction and flat-field corrections were handled with MIDAS (Grøsbol & Ponz 1985), and image centering and instrumental magnitudes with DAOPHOT 2.0 in MIDAS (Stetson 1987). The final transformations, including extinction correction and color transforms to the Johnson-Cousins standard system, were done with a version of the code SNOPY developed at ESO, properly modified to run on CCD data by Pizzuti (1991) and Mitton (1992).

The average precision of the standard sequences derived here is, for both regions, better than 0.05 mag for V, B-V, and $V-R_{\rm c}$.

2.1 The galactic plane field

The $BVR_{\rm c}$ CCD frames specifically taken for the photometric calibration of the GPR were calibrated using, as in-situ standards, those stars in Krzeminski & Serkowski (1967) within the $11'\times 11'$ field covered by the CCD (Table 2).

These photoelectric standards are all too bright ($V\le 12.22$) for a direct calibration of the frames down to $V\simeq 18$. To bridge the magnitude gap, we took frames of different exposures (1, 2, 10, 60 s in R; 2, 4, 20, 120 s in V; 4, 8, 40, 240 s in B) using field stars as standards for the deeper frames. Krzeminski and Serkowski only provide UBV photometry. Therefore, $R_{\rm c}$ magnitudes of the bright photometric calibrators were computed from spectral types, E(B-V), and V magnitudes as given in Krzeminski & Serkowski (1967), the $(V{-}R_{\rm c})_0$ intrinsic colors from Table 7 (p. 311) of Straizys (1992), and the ratios of red to blue reddening $E(V{-}R_{\rm c})/E(B{-}V)$ as published by Taylor (1986); these are summarized in Table 2.

  

Table 2: GPR. Primary photometric calibrators

The experimental color equations we found, which transform the CCD magnitudes b, v, and r into the standard ones, are:

$$\begin{eqnarray} V-v &=& 0.049(\pm 0.011) \cdot (B-V) + \zeta_V \\ B-V &=& 1.041... ..._{BV} \\ V-R_{\rm c} &=& 1.232(\pm 0.028) \cdot (v-r) + \zeta_{VR}\end{eqnarray}$$ (1) (2) (3)

and

$$\begin{eqnarray} V-v &=& 0.031(\pm 0.013) \cdot (B-V) + \zeta_V \\ B-V &=& 1.041... ..._{BV} \\ V-R_{\rm c} &=& 1.142(\pm 0.020) \cdot (v-r) + \zeta_{VR}\end{eqnarray}$$ (4) (5) (6)

for the second and fourth exposures, respectively; the two exposures were merged in the final list. The formal errors on the fitted value of the zero points $\zeta_i$ are less than 0.05 mag.

As an external check on the accuracy of these results, and in particular on that of the $V-R_{\rm c}$ color (being based on synthetic red magnitudes), we looked at the $(V{-}R_{\rm c})$ vs. (B-V) plot of the derived colors. Figure 1 shows these colors (dots) superimposed to the main sequence (solid line) obtained using the intrinsic $BVR_{\rm c}$ color data as given in Straizys (1992). Apart from the expected shift along the curve defined by the intrinsic colors, due to the strong interstellar absorption in this field (A_V = 4.0 mag/kpc), the observed colors have practically the same slope as that defined by the intrinsic colors. Again, this was expected as the selective reddening ratio $E(V{-}R_{\rm c})/E(B{-}V)$ is about the same as the natural slope of the intrinsic color sequence, and it shows that the $R_{\rm c}$ calibration is consistent with the observed B and V magnitudes. Any systematic effect on the red magnitudes would manifest itself as a translation along the $(V{-}R_{\rm c})$ axis.

  

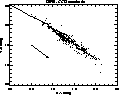Figure 1: GPR. Two-color diagram. The points show the colors as derived from the CCD data. The solid line represents the intrinsic colors of Straizys (1992), and the arrow the slope of the reddening

2.2 The North galactic pole field

For each of the three CCD fields imaged in the direction of the NGP region, we proceeded in a way similar to that adopted for the GPR region. To bridge the magnitude range needed for a proper calibration of the photographic photometry, we took four series of exposures for each bandpass used: 1, 2, 10, 60 s in $R_{\rm c}$, 2, 4, 20, 120 s in V, and 4, 8, 40, 240 s in B.

The low star density and a noticeable variation of the telescope point-spread-function (PSF) across the chip suggested the use of aperture photometry, instead of PSF fitting (which was the method of choice for the low latitude field) for the derivation of the instrumental magnitudes. In particular, we used the growth curve technique (Stetson 1990; Da Costa 1992) for the determination of the optimal software aperture.

The transformation to the standard Johnson-Cousins system was done via the usual method of observing a set of primary photometric standard stars at different air masses throughout the same night. Stars from Landolt (1992) in the magnitude range $12.116\le V\le 15.530$, and in the color ranges $0.516 \le (B-V) \le 1.344$, $0.351 \le (V-R_{\rm c})\le 0.897$, were used.

The best-fit to the color equations provided:

$$\begin{eqnarray} V-v &=& -0.010(\pm 0.028) \cdot (B-V) + \zeta_V \\ B-V &=& 1.15... ... + \zeta_{BV} \\ V-R &=& 1.125(\pm 0.045) \cdot (v-r) + \zeta_{VR}\end{eqnarray}$$ (7) (8) (9)

with internal errors on the zero points $\zeta_i$ of 0.05-0.06 mag.

The final list of faint photometric standard stars was derived from the second and fourth exposures. In the magnitude range covered by both exposures, proper averaging was applied.

  

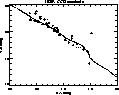Figure 2: NGP. Two-color diagram. Crosses, triangles and diamonds show the colors as derived from the CCD data for the central (I), North-East (II) and North-West (III) fields. The solid line represents the intrinsic colors of Straizys (1992)

As for the GPR, Fig. 2 shows the color-color plot for the NGP field with superimposed Straizys' unreddened main sequence. Besides the reliability of the photometric calibration, this plot confirms the predicted low reddening along this line of sight. (Visual inspection of the image shows that the outlier with $B-V\approx 1.5$ and $V-R\approx 0.5$ is a suspected double object and is not listed in the final table.)

Here, the CCD-based standard colors have been corrected for an offset of -0.04 and +0.05 mag in (B-V) and $(V{-}R_{\rm c})$ respectively. These offsets can be interpreted as the expected effect of the zero point errors in the transformation from instrumental to standard magnitude and colors. The correction on B-V was inferred from comparisons with independent UBV photometric catalogs (see Spagna et al. 1996 for details). The $\Delta(V{-}R_{\rm c})$ correction was derived directly from the color-color diagram, as the shift which best matches the observed and theoretical sequences.