5 Comparisons with other systems

5.1 High-resolution images

  

Table 2: A comparison between Johnson B-band total-magnitude values obtained from high-resolution galaxy images using different extrapolation systems

• $^{\rm a}$ T system extrapolation of aperture and/or surface photometry, RC3.
• $^{\rm b}$ Zwicky magnitude transformed to T system, RC3.
• $^{\rm c}$ Kron system extrapolation, Metcalfe et al. (1995) or this work.
• $^{\rm d}$ t system extrapolation, this work.

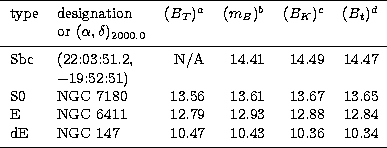
In Table 2, we have transformed those CCD-system total-magnitude estimates flagged with a superscript `b' symbol in Table 1 into Johnson or Cousins system magnitudes based on the colour equations of Metcalfe et al. (1995). Note that we did not invoke Metcalfe et al.'s magnitude values for any of the relevant galaxies, only their colour values when necessary.

It is clear from Table 2 that the agreement between the different systems for the objects considered is excellent. Note that for the three classical galaxies, the zero points on which the Kron-system and t-system values were based were the same, whilst those on which the T-system values were based were independent. In the case of the dwarf elliptical though, the T-system and t-system values were both based on the zero point of Kent (1987).

For the sake of completeness, we would very much have liked to include a dwarf galaxy whose n value is much greater than 1.0 in the comparisons performed in this subsection. However, we have not yet been able to obtain deep CCD images of a suitable galaxy. In any case, as mentioned in Sect. 2, there can be no doubt that such objects cannot be accommodated by the T system, which necessarily over-estimates their luminosities.

5.2 Low-resolution images

Whilst the agreement between the three systems is very good for the four resolved galaxy images already investigated, let us now consider what would happen if we attempted to estimate the total magnitudes of these same galaxies if they were, hypothetically, re-located at much greater distances from our galaxy. Clearly, seeing effects would become more significant than they were during the original observations. In fact, the effects can be understood from Fig. 1, if one interprets greater FWHM values as the same degree of seeing due to a particular galaxy being re-located to greater distances from us, and one re-scales the absolute radial-distance scales accordingly. For example, in the case of NGC 147, which is about 0.67 Mpc distant (Lee et al. 1993), Fig. 1(i-l inclusive) represents profiles under purely hypothetical atmospheric conditions in which the FWHM of the seeing discs are 60-480$^{\prime\prime}$, but also represents the same galaxy if re-located at a distance of 13.6 Mpc and observed under conditions with seeing discs of 0.$^{\prime\prime}$3-2.$^{\prime\prime}$FWHM. As one would expect, the profiles of more distant and/or physically smaller galaxies are more susceptible to distortion by seeing effects than those of nearby and/or physically larger systems.

  

Table 3: T-system total magnitude estimates based on the synthetic classical elliptical galaxy profiles$^{\rm a}$ plotted in Fig. 1 as a function of the FWHM of the seeing disc

• $^{\rm a}$ For the sake of consistency, we used the same isophotal weighting scheme as for the t-system profile fitting procedure.

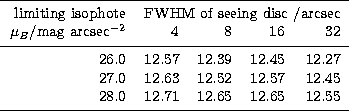
In the case of the t system, distortion of image profiles due to seeing effects can be accounted for, as was demonstrated in Sect. 4. However, because the T system assumes that a galaxy's surface-brightness profile (or the integrated luminosity equivalent) is only a function of morphological type and not of image resolution, it is therefore only applicable to highly-resolved galaxy images. As is evident from Table 3, if seeing effects are significant but not taken into account, this will generally result in an over-estimate of luminosity for a particular galaxy.

The Kron system, by contrast, does not make any prior assumption as to the profile shape of a target galaxy, though it does make a smaller assumption as to the shape of the curve representing the logarithmic derivative of the light-growth at large radial distances. We would therefore expect Kron-system total-magnitude scales to be very stable with respect to the size of the seeing disc, but there may of course still be room for small second order effects due to the assumption mentioned.

5.3 Images due to point sources

  

Table 4: Estimates of the total light contained under two typical (two-dimensional radially symmetric) Moffat surfaces, obtained by fitting different profile laws to different numbers of isophotal levels; the resulting values being quoted as linear fractions of the actual total-light values (which have both been set to unity)

• $^{\rm a}$ The depth of the simulated surface-photometry in terms of the number of isophotal levels (of 0.25 mag arcsec^-2 separation) fitted.

In order to test the applicability of the t system to images due to point sources, we simulated the surface photometry one might expect to obtain for two model point spread functions. The two model profiles adopted were based on Moffat functions using the original parameter values quoted by Moffat (1969) for traced stellar images on Hamburg Schmidt and the Lick 120-inch reflector photographic plates. The adopted parameter values were $\beta=4$ and $R=5\ 10^{-5}$ m for the Hamburg plates and $\beta=2.72$, and $R=1.12\ 10^{-4}$ m for the Lick plates. The brightest isophote in each case was taken to correspond to that radial distance, r, this time in metres, at which the surface brightness was 0.125 mag m^-2 fainter than the peak value at r=0. Radii were then computed for further (circular) isophotes that were multiples of 0.25 mag m^-2 fainter than the brightest isophote.

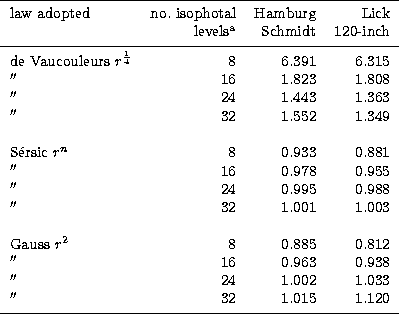
The results of attempts to fit not only Sérsic's law, but also the Gaussian and $r^{\frac{1}{4}}$ laws, to the brighter isophotes of these model profiles are shown in Table 4. For these fits, the adopted weighting scheme was: $\sigma_{\mu}=0.05+0.02(\mu_{0}-\mu)$, where $\mu_0$ is the peak central surface brightness at r=0 in units of mag m^-2. Note that although Moffat did not quote plate-scale values, we were still able to investigate the fractional differences between the extrapolated total-luminosity estimates and the true luminosities represented by the two-dimensional radially-symmetric Moffat surfaces.

From Table 4, it is clear that, as one would expect, the $r^{\frac{1}{4}}$ law always severely over-estimates the light due to a point-spread function represented by a Moffat profile. It is also evident from the same table that an extrapolation of Sérsic's model generally yields a significantly better estimate of the total light due to a typical point-spread function than does an extrapolation of a strictly Gaussian model.

In the above comparisons, we have of course applied a very stringent test to t-system and Gaussian-law extrapolations, by invoking pure Moffat functions to describe the unresolved images. In practice, as in the compilation of the VPC for example, the structures of the unresolved images should really be described by the product of three functions, the sampling function, a Moffat function and the smoothing function, all convolved with one another. Provided that the smoothing function is a single-component function that falls off steeply with increasing radial distance, such as a Gaussian function, better results should be obtainable using Sérsic's model (or even a strictly Gaussian model) than those tabulated in Table 4. This is because a pure Moffat function is less amenable to being described by a Sérsic function (or the Gaussian case thereof) than is a Moffat function that has been deliberately smoothed. The t system is therefore applicable to point-source galaxy images as well as resolved-galaxy images. While it cannot offer a perfect fit to a typical unsmoothed point-spread function, it does generally offer significantly better results than those that can be obtained by invoking a purely Gaussian model.