2 Kohonen maps

A Kohonen map is usually taken as a two-dimensional scene in which the observations are classified such that those which share related characteristics are located in the same zone of the map.

As an example of the application of the SOM method, Honkela et al. (1995) created a map of the fairy-tales of the Brothers Grimm. Word triplets were examined in this work, following removal of very frequent or very rare words. A triplet was used to provide a context for the middle word. The words in the text were classified without a priori syntactic or semantic categorization. The output map shows three clear zones where the set of nouns and verbs are separated by a more heterogenous zone constituted by prepositions, pronouns and adjectives.

A Kohonen map shares many properties with statistical (i) clustering methods, and (ii) dimensionality-reduction methods, such as principal components analysis and correspondence analysis. Murtagh & Hernández-Pajares (1995) present a range of comparisons illustrating these close links.

2.1 Creating a SOM Map

SOM maps are a particular type of neural network or pattern recognition method known as unsupervised learning. An SOM map is formed from a grid of neurons, also usually called nodes or units, to which the stimuli are presented. A stimulus is a vector of dimension d which describes the object (observation, entity, individual) to be classified. This vector could also be a description of the physical characteristics of the objects/stimuli. In this work, it will be based on characteristics such as the presence or absence of keywords attached to a document. Each unit of the grid is linked to the input vector (stimulus) by means of d synapses of weight w (Fig. 1). Thus each unit is associated with a vector of dimension d which contains the weights, w.

  

Figure 1: The Kohonen self-organizing feature map network scheme

2.2 The algorithm

The grid is initialized randomly.

2.2.1 The learning cycle

The learning cycle consists of the following steps.

1.

Present an input vector associated with a stimulus to the grid.

2.

Determine the winner node. This is the unit for which the associated vector is the most similar to the input vector.

$$\Vert \mbox{input} - \mbox{node}_{\mbox{winner}} \Vert = \min_i \Vert \mbox{input} - \mbox{node}_i \Vert$$

3.

Modify the weights w_i of the winner node, as well as those nearby, such that the associated vectors (the weight vectors) are as similar as possible to the input vector (p_i) presented to the grid.

$$w_i(t+1) = w(t) + h(r,t) (p_i - w_i(t)) \ \ \ \mbox{if} \ \ \ i \in \ \mbox{neighbourhood}$$

$$w_i(t+1) = w_i(t) \ \ \ \mbox{if} \ \ \ i \notin \ \mbox{neighbourhood}$$

where

$$h(r,t) = \alpha(t) v(r)$$

$\alpha(t)$ is the learning coefficient and v(r) is the neighbourhood function.

4.

Decrease the size of the neighbourhood of the winning nodes (the zone which contains neurons allowed to undergo modification).

5.

Decrease the learning coefficient, $\alpha(t)$, which controls the importance of the modifications applied to the weight vectors.

6.

Halt the learning when the learning coefficient is zero. Otherwise present another stimulus to the grid.

2.2.2 The neighbourhood function v(r)

The modification of vectors associated with the units is carried out in different ways depending on the position of the nodes with respect to the winner unit. The winning node will be the one whose vector will be potentially subjected to the most modification, while the more distant units will be less affected. The function v(r) will be maximal for r = 0 and will decrease when r increases (i.e. at increasing distance from the winner node). In this work we used a linear function (v(r)) which allows for inhibition of nodes which are distant from the winner node.

2.3 The results

SOM maps allow the classification of objects for which we do not have a priori information. Once the map is organised (i.e. once the learning has been accomplished), each object is classified at the location of its ``winner''. The use of a grid containing fewer units than objects to be classified allows the creation of density maps. For such a grid, the distances between the objects to be classified can be related to axis interval lengths.

2.4 Treatment of boundaries

The nodes at the edges of an SOM map are to be treated with care, since they do not have the usual number of neighbouring units. To insure the stability of the map configuration during successive learning cycles, we took the view that a node at a map edge has neighbours at other extremities of the map. Thus our map is a flattened version of a sphere, allowing for wrap-around, as represented in Fig. 2.

  

Figure 2: Left: the neighbourhood of the winner extends over the boundary of the grid. Right: the gray zone shows the neurons whose weights are to be modified during training

As long as the neighbourhood radius is not large, wrap-around neighbourhoods do not cause any problems. If, however, the neighbourhood were to extend back into itself, this would imply ambiguities where certain units would be considered as close neighbours in one direction, while being very distant in the opposite direction.

The user can obviously modify the map at will by moving the rows or columns horizontally or vertically. A row pushed out beyond an edge will reappear at the opposite side (Fig. 3). This reordering can be of benefit when an interesting zone is located near the map extremity.

  

Figure 3: Detail view of reconfiguring the neuron grid

2.5 Influence of number of network nodes

The size of the SOM map has a strong influence on the quality of the classification. The smaller the number of nodes in the network, the lower the resolution for the classification. The fraction of documents assigned to each node correspondingly increases. It can then become difficult for the user to examine the contents of each node when the node is linked to an overly long list of documents.

However, there is a practical limit to the number of nodes: a large number means long training. A compromise has to be found.

One possible strategy which we use to face this trade-off problem is to create another layer of maps (Luttrell 1989; Bhandarkar et al. 1977). The first network ``of reasonable size'' (to be further clarified below) is built and is trained using all stimuli. This network may be too small for an acceptable classification and some nodes may be linked to too many documents. Then, for each ``over-populated'' node of this map, termed the principal map, another network, termed secondary network or map, is created and linked to the principal map. Each secondary network is trained using the documents associated with the corresponding node of the principal map. The training of secondary maps is thus based on a limited number of documents, and not on all of them.

In this way, a map is created with as many nodes as necessary, while keeping the computational requirement under control.

2.6 Training time

Most of the computational requirement is due to the determination of the winner node corresponding to each input vector and to the modification of the vectors associated with neighbouring units of the winner nodes. The number of operations to be carried out is directly linked to the size of the network and to the number of stimuli:

$$\mbox{Determining the winners:} \ \sim N_{\rm stim}.N_{\rm unit}$$

$$\mbox{Updating of vectors:} \ \sim N_{\rm stim}.\sum_{R=1}^{R_{\rm max}}{R^{2}}$$

where $N_{\rm stim}$ et $N_{\rm unit}$ are respectively the number of stimuli and the number of units of the network. $R_{\rm max}$ and R are the values of the radius of the neighbourhood at the start (fixed) and in the course of the learning (varying). The second formula is somewhat simplified because we have assumed a linear decrease in R from $R_{\rm max}$ to 1, while the learning distribution might be different.

Let us compare now the ``classical'' and ``two-layer'' approaches. Let us take, as an example, a primary map of dimensions $15 \times 15$, for which each node is linked to a secondary map of dimensions $5 \times 5$. The size of the corresponding ``classical'' map is thus $75 \times 75$.

Determining the winning nodes:

-

In the case of the $75 \times 75$ map, the time required for determining the winner nodes is proportional to $5625 N_{\rm stim}$.

-

For the two-layer system, the time is reduced to

$$\underbrace{225 N_{\rm stim}}_{\scriptsize{\rm primary\ map}... ...}{N_k}}_{\scriptsize{\rm secondary\ maps}}=(225+25)N_{\rm stim}$$

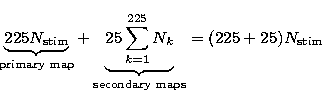
where N_k is the number of documents classified within the node k of the principal map.

The two-layer method is therefore about 5625/250 = 25 times faster than the classical method, in this case, at this step.

Updating the units:

-

In the case of the classical $75 \times 75$ map, the time required for updating the values of the winning nodes is proportional to

$$N_{\rm stim}.\sum_{R=37}^{1}{R^2}=17575 N_{\rm stim}$$

-

In the case of the two-layer method, we have

$$\underbrace{N_{\rm stim}.\sum_{R=7}^{1}{R^2}}_{\scriptsize{\... ...N_{k}.\sum_{R=2}^{1}{R^2})}}_{\scriptsize{\rm secondary\ map}}$$

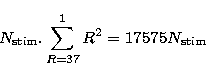
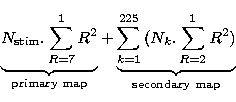
which gives

$$N_{\rm stim}(140+5) .$$

The results presented here are contrary to the claim made in Zavrel (1996) that the Kohonen map does not scale well. We have also found convergence properties, and in particular stability, not to give rise to undue difficulties. Other experiments concerning the stability of the results, described in Murtagh & Gopalan (1997), are in agreement with this finding.

To conclude, the association of a Kohonen secondary map with each node of a principal map, or with the over-populated nodes only, allows a high-quality classification of the stimuli with considerable improvement in the training time.

2.7 Weighting of index terms

The use of secondary maps for bibliography classification indicated early on the need for changing our mode of defining the document descriptors. We recall that the set of stimuli to be presented to the secondary map is the result of an earlier training. Therefore these stimuli are all more or less the same, and only differ by a small number of the descriptors present in the set. Often the documents are clustered around an over-burdened node. This is clearly not desirable since relevant information can be added by the secondary map in this case.

This behaviour is explained by the training principle: the descriptors or the index terms associated with the majority of the stimuli are those which occur most frequently, since the vectors associated with network nodes are modified to resemble the input vectors. During training, the corresponding components of these vectors take the largest values and therefore have the strongest weight. Finally, the classification of the documents is dominated by their relation to these majority descriptors. It is therefore not surprising that many documents are found associated with a few nodes.

The solution to this problem is to bypass the binary stimuli-vectors and to allow for vectors with non-integer components. Weights are used to specify the importance to be accorded to different descriptors. We used for this a simplification of the weighting method described by Salton (1989). This method uses n_i, the number of occurrences of descriptor number i in the set of documents to be classified in the secondary map; and N, the number of documents in this set to be classified in this way. The weight of descriptor i is then given by

$$w_{i}= \ln \left( \frac{N}{n_{i}} \right).$$

The input vectors are then normalized to prevent penalizing the stimuli associated with rare descriptors. The most frequent descriptors are downgraded, having small weights, which tend towards zero if they are present in all documents. By weighting the documents in this way, we were able to avoid the effect of accumulated stimuli at the same node. This assumes of course that the various stimuli are genuinely different.