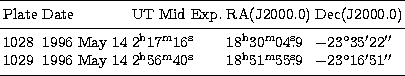2 Photographic observations

The orientation and scale of the CCD chip can easily be measured if there are sufficient stars of accurately known position on the same CCD images. To measure star positions in the area of sky crossed by Uranus during 1990 and 1991 we exposed two photographic plates with the Wide Field Camera (WFC) on the Jacobus Kapteyn Telescope (JKT); $28\hbox{$^\circ$}\; 45\hbox{$^\prime$}\; 39\hbox{$.\!\!^{\prime\prime}$}9 \;$ N $\; 17\hbox{$^\circ$}\; 52\hbox{$^\prime$}\; 41\hbox{$.\!\!^{\prime\prime}$}2 \;$ W $\; 2364\:$m. The plates (Table 1) were exposed at the f/8.06 Harmer-Wynne focus where the plate scale is $25\hbox{$.\!\!^{\prime\prime}$}67$/mm and the field diameter $1\hbox{$.\!\!^\circ$}5$,Harmer & Wynne (1977), Carter et al. (1995).

  

Table 1: Details of photographic plates

For both plates the emulsion was Kodak IIIaF hypersensitised by baking in Forming Gas for 2 hours at 65 $\hbox{$^\circ$}$C, the filter 4 mm RG630, and the exposure 32 mins. This reproduces the R band with effective wavelength 650 nm. The R band was chosen to minimise atmospheric dispersion as the plates were exposed at a zenith distance $\sim 50\hbox{$^\circ$}$.Experience gained from similar plates suggests that the faintest images of astrometric quality are $R \approx 17$.

The plates were measured on the RGO PDS in Cambridge at orientations of $0\hbox{$^\circ$}$ and $90\hbox{$^\circ$}$. The reference stars which were taken from the PPM catalogue (Bastian & Röser 1993) and the measures were reduced with a six coefficient fit after removing the distortion of the Harmer-Wynne design following Taylor et al. (1990). The ASTROM program written by Wallace (1994) was used for all reductions.

The 16 reference stars were measured at the beginning and end of both measuring runs so that there are four measures of each; thus the rms error of the measuring machine and the rms error of the catalogue can be separated and are presented in Table 2.

  

Table 2: Photographic measuring errors

The measuring error is the accuracy with which the machine can centre on an image. The rms error of the PPM is the goodness of fit of the measures to the PPM positions. The expected error is derived from the published errors in the PPM Catalogue. The last two values are expected to be the same; their difference is not statistically significant for samples of this size.

The plates were compared with the CCD images and 166 stars in common were identified and measured. As each programme star was measured twice the expected internal rms error in one co-ordinate is $0\hbox{$.\!\!^{\prime\prime}$}03$.There are only eight stars in common with the GSC1.2 (Morrison & McClean 1996).