7 Statistical results

The actual number of envelopes mapped in ¹²CO($J=1\rightarrow 0$) with combined data from the IRAM interferometer and the IRAM 30 m telescope and mapped in ¹²CO($J=2\rightarrow 1$) with the IRAM 30 m telescope is 46. Two objects have been mapped in ¹²CO($J=2\rightarrow 1$) only (CL Mon, HD 187885) and two in ¹²CO($J=1\rightarrow 0$) only (RY Dra and 19480+2504).

7.1 Table contents

The results of the ¹²CO($J=1\rightarrow 0$) and ¹²CO($J=2\rightarrow 1$) maps analysis are given for each object and summarized in Tables 4 and 5. The first column of Table 4 contains the abbreviated IRAS designation and the second gives the most common name. The next two columns show the equatorial coordinates (epoch J2000) of the source, obtained by fitting interferometric data alone, and the estimated errors. Column 5 lists either the flux density of the radio continuum at 112GHz or gives $5\sigma$ upper limits. Columns 6-11 and 12-17 tabulate the results obtained in the ($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) line emission, respectively: the terminal ¹²CO velocity of the envelope (i.e. the expansion velocity or the maximum projected velocity), the systemic velocity with respect to the local standard of rest, the spatially integrated flux density at the systemic velocity, the velocity integrated lined intensity, and the main beam temperatures as observed towards the star position. The epochs of observations for the interferometer are in Col. 12, for the 30 m telescope in Col. 17.

Table 5 lists the results of the gaussian fits. Columns 3-12 and 13-17 give the results for the ¹²CO($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) transitions, respectively. Columns 3-7 (index 1) tabulates the flux density, the major and minor sizes, the position angle (east to north) and the degree of asymmetry of the main envelope component. When a second component was fitted to the visibility profile, the results are given in Cols. 8-12 (index 2). The major axis is marked ``U" (unresolved) when the envelope was found to be roughly equal or less than the estimated beamsize of the 30 m telescope, and is marked ``?" when the data was to scarse or noisy to allow any size determination.

7.2 Atlas contents

The results of the ¹²CO($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) data analysis are presented at the end of the paper. There are two pages for each object, one for each transition. The pages are ordered by increasing right ascension. The page heading identifies the ¹²CO transition and the star's most common name and coding in equatorial coordinates (epoch B1950). Each page is divided in four panel rows:

row 1: while the three panels on top of the ¹²CO($J=1\rightarrow 0$) page show channel maps obtained from the combination of the interferometric and single-dish data, the panels on top of the ¹²CO($J=2\rightarrow 1$) page show channel maps obtained from single-dish data alone. The integrated velocity intervals for the panels are roughly $-V_{\rm exp} \le V \le -V_{\rm exp}/3$, $-V_{\rm exp}/3 \le V \le V_{\rm exp}/3$ and $V_{\rm exp}/3 \le V \le V_{\rm exp}$. The range of velocities used for the central panel is indicated in the integrated flux panel. The synthesized beam obtained from the combination of the two data sets is shown in the inset. The contour levels are marked in the wedge on top of each panel and start at five sigma. Map units are in Jy/beam and K km/s. The ¹²CO($J=2\rightarrow 1$) maps were not recentered to zero offset, the central position being undetermined deviations up to 2.5$^{\prime\prime}$ are possible.

row 2: the left panel ¹²CO($J=1\rightarrow 0$) shows the integrated flux obtained at zero spacing by fitting gaussian profiles to the visibilities. The error bar is set to the one sigma noise level W^-1/2, where W is the weight of the single-dish data at zero spacing. The central panel shows the global visibility profile for velocities in the $-V_{\rm exp}/3 \le V \le V_{\rm exp}/3$ range and gaussian curves representing the major and minor axes of the fitted profiles. The uv-coverage is shown to the right.

The left panel ¹²CO($J=2\rightarrow 1$) shows the flux integrated over the channel maps (continuous line) and the flux towards the star position (dashed line). The central and right panels show the apparent full widths along the major and minor axes, prior to beam deconvolution.

row 3: the major and minor axes of the gaussians which were fitted to the global visibility profile are shown in the left and central panels of the ¹²CO($J=1\rightarrow 0$) page. The asymmetry parameter (L-l)/(L+l), where L and l are the major and minor axes respectively, is shown to the right.

The ¹²CO($J=2\rightarrow 1$) left panel shows the radial intensity profile (continuous line) and the presumed shape of the single-dish beam (dashed line). Positional offsets in right ascension and declination where obtained by fitting gaussians to the channel maps and are given in the central and right panels.

row 4: the ¹²CO($J=1\rightarrow 0$) panel displays positional offsets in right ascension and declination (left and center) and position angle (north to east) as obtained by fitting gaussians to the global visibility profiles.

The ¹²CO($J=2\rightarrow 1$) panel lists the name of the source, the equatorial coordinates (epoch J2000) obtained by fitting only interferometric data, the interferometric on-target time for equivalent single-baseline observations, the number of snapshots, the synthesized beam and the one sigma noise level in the ¹²CO($J=1\rightarrow 0$) channel maps shown in the top panel row, the primary calibrators, the amount of flux retrieved by the interferometer, and it summarizes the results found in both the ¹²CO($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) transitions.

 

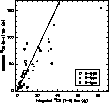Figure 2: Comparison of integrated ($J=2\rightarrow 1$) vs. ($J=1\rightarrow 0$) 12CO fluxes. The dotted line traces envelopes in the optically thick F230/F115 = 4 limit

We have not included the low-declination source VX Sgr in the atlas and in Table 5, as the data quality was too marginal.

7.3 Statistical error estimates

Positional errors are normally distributed, whereas errors in flux density and width, as a consequence of their positivity, are not. To quantify the uncertainties in position, width and flux we have carried out Monte-Carlo simulations. We modeled circular gaussian profiles sampled at twice the angular resolution of the telescope with normally distributed noise. The results (see also the Appendix) show that the probability to underestimate the width of a gaussian depends on the signal-to-noise ratio in the samples. At signal-to-noise ratios larger than 10 the probability to underestimate or overestimate the width is almost even, the probability distributions become gaussian and the uncertainties can well be approximated by standard deviations. Similar results are found for the flux density estimates.

7.4 Integrated fluxes

We have first compared the relative ¹²CO($J=2\rightarrow 1$) / ($J=1\rightarrow 0$) intensities in our source sample. In Fig. 2 we show the integrated flux of both lines (Sects. 4.2, 6.2); the dotted line represents the expected ratio for optically thick emission and a common excitation temperature, which is equal to 4. As we see, the optically thick ratio agrees well with observations in most cases. In two oxygen rich objects, RS Cnc and R Cas, the observed ratio is higher than expected. The CO profiles in these stars are peculiar and do not show the parabolic or flat-topped shape expected for optically thick lines. It is then possible that in RS Cnc and R Cas the J-dependence of the opacity leads to the observed high line ratio. In other objects, like the carbon rich CIT 6 and the oxygen rich IRC+20326, the ($J=2\rightarrow 1$) / ($J=1\rightarrow 0$) relative intensity is smaller than 4. This is not likely to be due to pure opacity effects but to a particularly low excitation of the ($J=2\rightarrow 1$) line. Note that it is not impossible that in certain cases the excitation and line-strength effects cancel, which could yield line ratios close to the optically thick limit. However, the systematic presence of optically thick emission in the ¹²CO lines is confirmed by the general properties of the observed profile shapes (Sects. 4.3 and 6.3) and we conclude that such departures from the optically thick situation are rare.

There certainly is a strong correlation (see Fig. 4) between the CO luminosity and the physical extent of the envelope. Such a correlation may be partially due to the effects of the errors in the assumed distance on these parameters, since the distance value enters the determination of both the luminosity and linear size. However, such errors are not expected to exceed a factor 2, which is not enough to explain the empirical relation. Moreover, a correlation between the envelope thickness and the radius of the CO emitting region is expected if this is mainly given by CO photodissociation (see below). We accordingly think that the relation depicted in Fig. 4 between the CO luminosity and the CO radius is, at least partially, real. We also can see in Fig. 4 that oxygen rich envelopes seem to be less extended and luminous than carbon rich ones. This could be a direct consequence of the selection criteria used to set up the star sample. In fact, the selected oxygen rich sample is on average $3\times$ closer than the carbon rich one, which consequently resulted in a typically $10\times$ more luminous than the carbon star sample. However, we did not select nearby oxygen rich stars and farther carbon rich objects, we just chose the most intense (and better studied) sources. This distance factor mainly reflects the fact that oxygen rich stars are more abundant and then can be found closer to us. Again, if the distance errors are not very large, the separation between the different groups in Fig. 4 is real and we must conclude that absolute CO luminosities are larger in carbon rich stars.

 

Figure 3: Comparison of the envelope sizes in the 12CO($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) line emission. In the density bounded limit (dotted line), when the envelope runs out of 12CO molecules, both the ($J=1\rightarrow 0$) and ($J=2\rightarrow 1$) transitions trace the same regions. The size of envelopes smaller than the 13$^{\prime\prime}$ beam of the 30 m telescope is generally overestimated

7.5 Expansion velocities

We have measured the ¹²CO($J=2\rightarrow 1$) and, when available, the ($J=1\rightarrow 0$) terminal velocity for all the circumstellar shells in our sample. The expansion velocities are, as expected, significantly similar for both CO lines. Only in ten objects the differences exceed 10%, and only in three stars, V CrB, T Cep and R Cas, the differences exceed 20%. In all these cases the difference between the expansion velocities derived from the ¹²CO($J=1\rightarrow 0$) line and from the ($J=2\rightarrow 1$) line can be considered as negligible due to the noise level, uncertainties in the baselines or lack for spectral resolution. V CrB and T Cep show weak and narrow CO lines which, particularly at 115GHz, makes difficult a good measurement of the line width. In spite of the peculiar profiles of R Cas which are quite different in both lines, a close inspection reveals again that the adoption of the same FWHP for both lines would not be incompatible with our data.

Although most sources show, as we have mentioned, the rounded or flat-topped profiles characteristic of circumstellar envelopes, anomalies are (at some level) present in a non-negligible number of stars. Some sources show more or less prominent spikes (U Cam, RS Cnc, R Cas, OH127.8+0.0, 04307+6210, S Cep) or relatively intense wings (M1-92, IRC+10420). In some cases, like U Cam, the profile seems in fact to be composite due to the particular structure of the envelope. Except for the two peculiar sources M1-92 and IRC+10420 with expansion velocities well above 25kms^-1, most of the velocities seem to fall all over the range found for AGB envelopes. M1-92 is known to present a high-velocity bipolar outflow that contributes to most of the profile width. This is probably also the case of IRC+10420. Both sources are described more in detail in Sect. 8.

 

Figure 4: CO luminosity vs. linear size for oxygen, carbon and S ([C/O] $\sim 1$) chemical types

7.6 Sizes and asymmetries

The envelope sizes measured in both lines are compared in Fig. 3. As we see, many stars show size ratios close to 1, as expected if the observed radii were given by a cut-off of the CO density at a given point. A certain number of stars, however, shows a somewhat larger size in the ($J=1\rightarrow 0$) line, which must be due to level population effects, since this line is of course easier to excite (in contrast opacity effects would lead to larger sizes in the ($J=2\rightarrow 1$) line). This conclusion is strengthened by the fact that most sources showing a significant discrepancy with the hypothesis of a common spatial cut-off for both lines, like CIT 6 and IRC+20326, also show a low ($J=2\rightarrow 1$) to ($J=1\rightarrow 0$) ratio. But we must note that others, in particular IRC+40540, are anomalous in relative size but not in relative intensity: IRC+40540 which is carbon rich, shows clearly parabolic CO profiles (see also notes on individual envelopes).

Most envelopes are found to show a significantly circular appearance. However, the global visibility profiles show that there is a non-negligible number of stars with peculiar circumstellar envelopes. It appears that many of these are surrounded by an inner envelope and an outer shell with morphologies that are not easily interpreted owing to the limited resolution achieved here. The bulk of the CO emission is in general found in the outer envelope which mostly appears spherical symmetric. The presence of an inner envelope, in some case indirectly suggested by a central tip in the spectral profile, suggests quite a substantial, if not abrupt, change in the mass loss rate in the envelopes of these stars testifying for a thermally pulsing activity. Some of these stars may already have left the AGB.

 

Figure 5: Comparison of measured sizes and calculated photodissociation radii in 31 envelopes. Photodissociation radii are calculated according to Loup et al. (1993). The dotted line is a linear fit (see Eq. 7)

Another finding is that a fairly large number of these envelopes shows a more or less pronounced asymmetry. The ¹²CO($J=2\rightarrow 1$) observations firmly establish the existence of a pronounced morphological asymmetry in the outer envelope of RAFGL 2155 and $\chi\,$Cyg, an asymmetry which is likely to be due to an anisotropic interstellar UV radiation field. In some objects, however, departure from sphericity occurs already in the innermost regions. This is in particular the case of the envelopes around RAFGL 3068 and IRC+40540, and possibly also around RAFGL 3099 (not indicated in Table 5). As shown in Table 5 and in the atlas, there are hints for developing asymmetries in many other stars, but the limited dynamical range hardly allows to draw clear conclusions.

7.7 Mass loss rates and photodissociation radii

We have used our ¹²CO($J=1\rightarrow 0$) data to perform a self-consistent calculation of the envelope mass loss rate $\dot{M}$ and photodissociation radius $R_{\rm CO}$, following the method described by Loup et al. (1993). The input parameters are:

1:

the envelope expansion velocity measured in ¹²CO($J=1\rightarrow 0$) and listed in Table 4,

2:

the distance of the star derived from the bolometric fluxes, as given by Loup et al. (1993 - Table 2 herein),

3:

the main beam temperature of the ¹²CO($J=1\rightarrow 0$) line as seen by a 7meter telescope (the calculation assumes that the envelope is unresolved) which we derive from the integrated ¹²CO($J=1\rightarrow 0$) flux (Table 4).

4:

the fractional CO abundance which was assumed to be constant and equal to $5\,10^{-4}$ for oxygen rich stars and 10^-3 for carbon rich stars and S-type stars (Zuckerman & Dick 1986).

We show in Table 3 the calculated photodissociation radii and mass loss rates, together with the assumed distances and some other properties. In Fig. 5 we show the comparison of the computed photodissociation radii of these envelopes, $R_{\rm CO}$ and their measured half-maximum radii, $\theta_{\rm CO}$. The correlation between both parameters is obviously significant.

In our procedure, the photodissociation radius is calculated from the CO total intensity (through the mass loss rate), therefore Fig. 4 reveals the existence of a correlation between the CO luminosity and the envelope size. In the case of optically thick emission, a relation of this kind can be expected, the radius being approximately identified with the point at which the line emission becomes optically thin and from which the emission starts decreasing sharply. However, in such a case the extent of the ($J=2\rightarrow 1$) line, which is always the most opaque, would have systematically shown a larger size than the ($J=1\rightarrow 0$) line, which is not the case in our data, see Sect. 7.4. Accordingly we conclude that the correlation shown in Fig. 5 indicates that the effects of photodissociation dominate the CO envelope size.

It is also noticeable in Fig. 5 that the measured envelope radius is always smaller than the calculated photodissociation radius. This is indeed expected, as the radius $\theta_{\rm CO}$ is equivalent to the size of the envelope at half the maximum intensity (see Sect. 6.4) whereas the photodissociation radius $R_{\rm CO}$ delimits a spherical region around the star in which the total mass of CO molecules is contained. The size of this region is mainly given by the intensity of the interstellar UV radiation field and the mass loss rate, since the molecule shielding from the external field depends on the envelope opacity.

Unquestionably, the mass loss processes that take place are certainly not smooth, steady and spherical in all the circumstellar envelopes of the sample. However, except for RY Dra, V814Her, RAFGL 2155, $\chi\,$Cyg and IRC+40540 which are slightly asymmetric at larger scales, for U Cam which has a detached shell, and for all envelopes with a hint for asymmetry (see Table 5), all other envelopes in the sample can reasonably be considered as spherical from an observational point of view and the simple model described above was applied to them.

Thus, leaving aside all envelopes of non-spherical appearance, we derived from a sample of 31 stars an empirical formula with which we estimate the photodissociation radius $R_{\rm CO}$ of an envelope from the measured CO radius $\theta_{\rm CO}$ at half maximum intensity

$$R_{\rm CO} = 1.5 \times \left [ \frac{\theta_{\rm CO}}{''} \right ] + 8.4''.$$ (7)

Even though, this relation (dotted line in Fig. 5) may not be too appropriate for estimating the photodissociation radius of an envelope, we have subsequently used it to compute the photodissociation radius of envelopes of, to our knowledge, unknown distances. Accordingly, by reversing the computational scheme described by Loup et al. (1993), we derived estimates for the mass loss rates and the distances of IRC+10420, 19480+2504, 20028+3910, HD 235858 and 23321+6545 (see Table 3). The calculations, however, were inconclusive for IK Tau and CIT 6, the last one showing hints for an asymmetric structure.

7.8 Non-detections and marginal detections

We have already seen in Table 2 that for 7 sources the quality of our data did not allow a proper interpretation. In some cases, galactic contamination was important, in others the CO emission was too weak. For OH39.7+1.5 and OH104.9+2.4 both contamination and weak emission are noticed. AC Her was not detected, we therefore do not confirm a previous tentative detection (Alcolea & Bujarrabal 1991) at a level of $\mbox{$T_{\rm MB}$}\mbox{($2\rightarrow 1$)}\sim 0.1\,$K, although our noise rms at this frequency is about 0.04K, not low enough to draw definitive conclusions. In some sources like R LMi and $\mu$Cep the ($J=2\rightarrow 1$) line is intense, but the ($J=1\rightarrow 0$) emission is too weak. In R LMi our $\mbox{$T_{\rm MB}$}\sim 0.1\,$K is compatible with the data by Bujarrabal et al. (1989). Le Borgne & Mauron (1989) give an intensity $\mbox{$T_{\rm MB}$}\mbox{($2\rightarrow 1$)}\sim 0.15\,$K for $\mu$Cep. Our data confirm this figure, but we found the ($1\rightarrow 0$) line too weak ($\sim 0.04\,$K) to be accurately mapped. We only show CL Mon in the ($J=2\rightarrow 1$) emission, the ($J=1\rightarrow 0$) data was too scarse.