4 Data analysis: $\bf ^{12}$CO($\bf J=2\rightarrow 1$)

4.1 Positions

The envelope central positions adopted to perform the ¹²CO($J=2\rightarrow 1$) observations are those reported by Loup et al. 1993. Due to pointing uncertainties and to the shift-and-add technique used to combine several maps, discrepancies between these coordinates and the actual map centers are meaningless. In the position-velocity diagrams, however, the zero position of the ¹²CO($J=2\rightarrow 1$) maps is chosen to correspond to the maximum of the ¹²CO($J=2\rightarrow 1$) emission.

4.2 Fluxes and main beam temperatures

The ¹²CO($J=2\rightarrow 1$) main beam temperature $T_{\rm MB}$ reported in the parameter summary of each envelope and in Table 4 is the average of the three central 1MHz channels in the spectral profile observed towards the envelope center. Channels affected by a galactic CO contribution have been omitted.

The flux density reported in the summary and in Table 4 is the average value of the three central channels in the spatially integrated ¹²CO($J=2\rightarrow 1$) spectral profile S(v) of each envelope. The integrated flux density profile has been obtained by adding the spectra with a uniform weight on a regular grid with a spacing d. The flux spectrum in Jy is given by

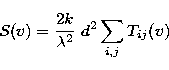$$S(v) = \frac{2 k}{\lambda^2} ~d^2 \sum_{i,j} T_{ij}(v)$$ (1)

where T_ij(v) is the main beam temperature observed at velocity v and positions (i,j), and where the grid spacing d expressed in radians is either 7.5'' or 5'' depending on the map, and k is the Boltzmann constant.

A comparison of the spatially integrated flux spectrum S(v) with the flux spectrum collected in the telescope beam towards the envelope central position, S₀(v), allows comparison of the envelope extent with the beam size: if both fluxes coincide, the envelope is unresolved by the telescope beam. For a gaussian beam of half power beam width h (in radians), the relation between the main beam temperature profile T₀₀(v) observed towards the envelope center and the flux spectrum in the central beam S₀(v) is

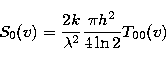$$S_0(v) = \frac{2 k}{\lambda^2} \frac{\pi h^2}{4 \ln 2} T_{00}(v)$$ (2)

which is equivalent to a conversion factor of 7.35Jy/K for the ¹²CO($J=2\rightarrow 1$) line observed at the 30 m telescope. Both flux spectra, integrated S(v) and central S₀(v) are plotted for comparison for each envelope (see Atlas). The 30 m telescope half power beam width at 230GHz, was estimated to be 13$^{\prime\prime}$ $\pm$ 1.5$^{\prime\prime}$, including beam smearing effects due to tracking errors.

We also give in Table 4 the total ¹²CO($J=2\rightarrow 1$) emission of the envelope (i.e. the flux integrated both spatially and over velocity).

4.3 Velocities and line shapes

The star systemic velocity $V_{\rm lsr}$ and the envelope expansion velocity $V_{\rm exp}$ have been derived from the full width at zero level (FWZL) of the ¹²CO($J=2\rightarrow 1$) lines. To minimize the effect of noise on the derivation of the FWZL, we have defined as the extreme line channels those for which the 20% to 90% intensity contours still show a centrally peaked pattern. The resulting velocities are given in the parameters list of each envelope and in Table 4. The errors are typically one channel half-width (1.3kms^-1 for most envelopes, 0.7kms^-1 for the 8 narrow line envelopes mentioned above).

We must keep in mind that this calculation of the expansion velocity tends to overestimate the true value of this parameter when the line profiles present conspicuous wings, the origin of which is expected to be related to local velocity dispersion or to the presence of bipolar outflows independent of the general envelope expansion. Fitting a truncated parabola systematically leads in such cases to lower estimates of the expansion velocity. This discrepancy can be significant in stars with low expansion velocities. In particular for objects in which the emission of the bipolar outflows is dominant, the meaning of an expansion velocity determined in this way, is just the maximal projection on the light of sight of the axial velocity.

Most envelopes present sharp-edged and round-topped lines, as expected for optically thick emission coming from a spherically expanding envelope. In a few cases (OH127.8+0.0, U Cam, S Cep IRC+60427) an interstellar ¹²CO($J=2\rightarrow 1$) contribution appears as a narrow peak or dip in the spectrum. As far as the signal to noise ratio of the data allows to conclude, some envelopes show ``unusual'' line shapes, with wings or shoulders, which suggest changes in the mass loss activity of these stars (see for instance U Cam, T Dra, RS Cnc and M1-92).

4.4 Sizes and asymmetries

To derive a more quantitative estimate of the envelope size in the ¹²CO($J=2\rightarrow 1$) line, we have fitted as a function of the velocity channel a 2D gaussian to the observed spatial distribution. Plots of the fitted minor and major axis (without beam deconvolution) and of the centroid shifts relative to the mean centroid position are shown for each envelope as a function of the channel velocity.

In a spherical expanding envelope with a constant (or monotonically increasing) radial velocity, the radius of the region emitting at a given radial velocity V_z or -V_z with respect to the systemic velocity is proportional to $\sqrt{1-(V_z/V_{\rm exp})^2}$. A decrease of this radius with the absolute value of V_z is, therefore, expected. As shown in the figures, such a behaviour is indeed observed in most sources, although the uncertainties in the measured size is high.

Once deconvolved from the telescope beam (h), the fitted major and minor (M and m) axes averaged over the three central channel maps provide a measure of the envelope size (L and l)

$$L = \sqrt{M^2 - h^2} \mbox{\hskip1cm} l = \sqrt{m^2 - h^2}$$ (3)

and a quantitative estimate of its asymmetry, given by the parameter

f = (L-l)/(L+l).

We have carried out a worst-case beam deconvolution to filter out envelopes with intrinsic elliptical shapes and mask out those whose asymmetry is possibly due to beam distortion. For this deconvolution, the telescope beam was assumed to be elliptical ($14.5'' \times 11.5''$) and its position angle was made to coincide with the position angle of the gaussian fit. This deconvolution provides a lower limit $L_{\rm min}$ to the actual envelope major axis and an upper limit $l_{\rm max}$ to its actual minor axis. We have then performed a conservative selection of the ``non-spherical'' envelopes, considering that any real departure from circular symmetry shows up even in the lower limit to the asymmetry parameter $f_{\rm min}$ given by

$$f_{\rm min} = (L_{\rm min}-l_{\rm max})/(L_{\rm min}+l_{\rm max}).$$ (5)

When $f_{\rm min}$ is lower than 0.1, which corresponds to a difference smaller than 20% between the axis limits, or when the sizes L and l are not determined with better accuracy than 5$\sigma$, the envelope is considered as spherical. We choose such a highly conservative limit to rule out any asymmetry due to possible uncertainties in the determination of the telescope beam or of the envelope sizes. In such a case, we give a single size in the identification panel of each star and in Table 5, which is the average of the fitted axes deconvolved by a circular beam of width h=13''

$$s = \sqrt{(M+m)^2/4 - h^2}.$$ (6)

Otherwise, the envelope is considered as asymmetric. Table 5 contains the envelope deconvolved minor l and major L axis (assuming a circular beam h) and the resulting asymmetry parameter f.

In addition, the plot of the envelope emission centroid versus velocity provides informations on the geometry and kinematics: for a spherically expanding envelope the centroid is expected to keep the same position at any velocity. On the other hand, if there is departure from overall spherical symmetry, the centroid is expected to move along an axis of symmetry. This behaviour is particularly obvious for RS Cnc, M1-92 and R Cas but exists also possibly for a few other envelopes, namely for Y CVn, $\chi$ Cyg, T Cep, IRC+40540 and IRC+60427.