The aim of the
calculation described here is to derive a quantity
to be maximized in order to obtain the optimal screening. This
quantity (hereafter the efficiency function) is defined as the ratio of
a source signal to noise ratio computed in a time screened
observation (
) and in the entire unscreened observation
(
), as a function of the amount of rejected exposure time.
We define a circular source cell and an annular background
cell, whose sizes are related to the local PSF.
The following quantities refer to the unscreened observation:
C = total counts in the detection cell (measured)
T = total counts in the background cell (measured)
S = source counts
B = background counts in the detection cell
= fraction of source counts in the detection cell
= fraction of source counts in the background cell
r = ratio of the background to detection cell area.
We can thus write, following the recipe of Harnden et al.
(1984) and Kashyap et al. (1994):
With simple algebra we can obtain from Eqs. (1 (click here)) and
(2 (click here)) the following expression for the source counts:
Adopting Poissonian statistics on the measured quantities C and T we
can also write the standard deviation on the source counts as:
Using the above equations, we can now write the signal to noise ratio
of the source for the unscreened observation in terms of S and B:
If a fraction x of the total observation time is screened out, the
expressions for screened C and T becomes:
where B(x), the total background present in the screened
observation, is equal to B (Eqs. (1 (click here)) and
(2 (click here))) for x equal zero (unscreened observation). The source is
assumed to be constant over the observation.
Analogously to what we have done for the unscreened observation we can
derive the screened SNR:
Using Eqs. (6 (click here)) and (7 (click here)), this becomes:
We can now define the efficiency function 
= 
to be maximized in order to obtain the
optimal screening of the observation under analysis.
For further discussions it is useful to rewrite the above equation
to stress the dependence of the
efficiency function on the ratios B/S:
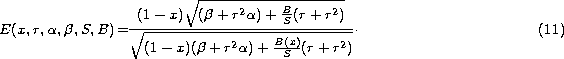
The parameters r, , and depend on the geometry of the
source and background cells and can be tabulated once the PSF of the
instrument is known as a function of the off-axis angle at a given energy
(or for a given input source spectrum).
We point out that this formalism is very general with respect to the
choice of the geometry of the source and background cells, and, in
addition, it is independent from the shape of the instrumental
PSF.