

Up: Photometry with adaptive
When trying to detect a faint structure around a star, either
a companion or an extended object, the easiest solution is to
subtract a point spread function, properly scaled and placed, from
the image of the main star. This procedure should theoretically remove
the light from the star and leave only the surrounding structures.
But here again some problems appear. The adaptive optics PSF is
the sum of two components: a diffraction-limited core surrounded
by a large halo due to variations of uncorrected high order modes
and imperfectly corrected low order modes.
This halo is therefore affected by strong variations with time
which are independent of the fluctuations of the central core.
These variations are even higher when two different objects are
compared because of the halo's dependence on parameters like
the brightness of the guide star.
To assess the limits for detection of a faint companion next to
a star, we used observed images of the single stars HR 2019 and HR 2076,
and subtracted one from the other.
For each image of HR2019, the integration time was 75 seconds,
the signal to noise ratio 7500 and the Strehl ratio 0.26.
For HR2076, these parameters were respectively 200 seconds,
10000 and 0.22. The delay between the two sets of images was 10
minutes. The subtraction method was applied to four
different couples of images in order to obtain different residuals.
Finally, we computed the standard deviation of these
residuals. To work out the average detection limit for a point like
object at a given distance of a bright star, we computed an azimuthally
averaged radial profile of the standard deviation of the different
residuals.
Figure 5 (click here) shows the radial
dependence of the detection limit. The full line corresponds
to the profile a star. The dotted line shows the radial profile of
the standard deviation of the four different residuals. For example,
we could detect on this basis
a companion fainter by about 7 magnitude at 1 arcsec
from the main star and fainter by more than 9 magnitudes at 2 arcsecs. This
result is in excellent agreement with the observations by Tessier (1995).
Note that far from the star (more than about 2
arcsec), the uncertainties are dominated by readout and sky noises.
An important point is that Fig. 5 shows
azimuthally averaged profiles. But the shape of the PSF is
far from having a circular symmetry. Lots of
non-axisymmetric small features appear, especially on the first diffraction
rings. Figure 5 should therefore be considered as an
over-optimistic estimate.
As an illustration of this method, we used adaptive optics data
taken on January 21st 1996 to
look for a possible companion to the star Betelgeuse. We subtracted
the images of different calibration stars from images of Betelgeuse.
No companion was visible down to the approximate limits indicated above.
Near to the star, the main problem was the presence of several
residual features whose position and intensity changed depending
on the calibration star used. One of these features stood out by
being always present at a position approximately constant.
If this feature were real, it would lie at about
0.5 arcsec to the south-west from Betelgeuse
and be 4.5 magnitude fainter. These data would be
consistent with a reported detection by Karovska et al. (1986) using
speckle observations. More details are given in Esslinger (1997).

Figure 5: Three radial profiles (in magnitude
and relative to the main star). The full line is the
profile of the star before subtraction. The dotted line
shows the radial profile of the standard deviation
of four different residuals.
This gives us the limiting magnitude for detection of a companion
at a given distance from the main star. The dashed line
(the lowest) corresponds to the standard deviation of a set of four images
taken on the same star
The previous test gives us an estimate of the global noise
affecting the subtraction procedure. It would be interesting
to work out the part due to the each main cause of noise.
With this aim in mind, we compute the standard deviation of
our set of 75-second exposures of HR 2019. This gives us the
detection limit if we only had to deal with variations of high
order modes and photon noise, and did not have the difficulty
of mismatch between PSFs from different stars.
The radial dependence of this limit
corresponds to the dashed line in Fig. 5 (click here).
This shows that the main source of error in our procedure
is indeed the variation of the PSF between the observations of the
science object and the reference star, confirming the results
by Tessier (1995).
We can also compare the relative contribution of photon noise compared
to the noise introduced by uncorrected or imperfectly corrected modes.
We can work out the photon noise from the number of photons per pixel
in the original image at a given distance from the peak. We find
for instance that, at the centre of the PSF, the level of photon noise
is about 7 magnitudes fainter than the peak intensity, thus 3 to 4
magnitudes fainter than the dashed line in Fig. 4. At a distance of
1 arcsec, photon noise is 10 magnitudes fainter than the peak intensity
and thus 1 magnitude below the same line. From this, we see that photon
noise is usually not important compared to the noise introduced by
uncorrected or imperfectly corrected modes.
These results are obtained in a direct mode. Obviously the search
for faint structures around a bright object can be much improved
by using a coronagraph. For example, Beuzit et al. (1997) used a coronagraph
with the Adonis system to study the circumstellar disk around Beta
Pictoris. In their observations, they would have been able to
detect a companion fainter by 11 magnitude at 1 arcsec and by
13 magnitudes at 2 arcsecs. This is an improvement of 4 magnitudes
compared to our results.
The subtraction procedure can be used to carry out photometric
measurements. Another possibility is to use a photometric method
designed for such cases: point spread function
fitting, as for example in DAOPHOT (Stetson 1987).
To assess the accuracy of photometry in this case,
we took images of the star HD5980 and its calibration star SAO255763
observed in December 1995 in the K band.
For HD5980, the integration time was 200 seconds,
the signal to noise ratio was 7000 and the Strehl ratio 0.32.
For SAO255763, these parameters were respectively 120 seconds,
45000 and 0.35. The delay between the images of the two objects
was 20 minutes and the pixel scale 0.050 arcsec.
With the image of HD5980, we artificially created an image of a main star
and its faint companion situated at a given distance and with a given
difference in magnitude.
The position of the companion was chosen to avoid the diffraction
spikes of the main star and to limit the influence of the other residual
features. We also performed the same procedure on images of
Betelgeuse and its calibration star HR2076.
The integration time for the images of Betelgeuse and HR2076
were respectively 6 and 200 seconds, the signal to noise ratios
25000 and 10000, and the Strehl ratio 0.22 for both objects.
The delay between the two observations was 10 minutes
and the pixel scale 0.035 arcsec.
We then applied the point spread function fitting algorithm DAOPHOT
to these images, providing it with an image of
the right calibration star. Comparing the result of DAOPHOT
and the known magnitude of the companion then enabled us to
work out the error in the magnitude estimation. As a comparison,
we also performed the same procedure with other stars but
no significant differences appeared in the results.
Figures 6 (click here) and 7 (click here) present results
of such investigations as contour plots. They show, for given separations
and differences in magnitude, the error which is made
in the magnitude estimated by DAOPHOT.
Figure 6 was created using an image of Betelgeuse
and Fig. 7 using an image of HD5980.
For Betelgeuse, we varied the separation from 0.25 to 1.98 arcsec with a
step of 0.25 arcsec. In the case of HD5980, this was done for a separation
between 0.21 and 2.12 arcsec with a step of 0.21 (the difference is mainly
due to the different pixel size). In both cases, we considered differences
in magnitude between 0 and 10 with a step of 1.25 magnitude.
The contour plots were smoothed to minimise the small irregularities
induced by residual features in the PSF.
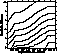
Figure 6: Error in the photometry of a faint companion as a function
of the distance and the difference in magnitude. The original image was
created with an image of Betelgeuse and DAOPHOT used an image of HR2076.
The contours are 0.001 (1), 0.003 (2),
0.01 (3), 0.03 (4), 0.1 (5), 0.3 (6), 1 (7) and 3 (8) magnitudes

Figure 7: Error in the photometry of a faint companion as a function
of the distance and the difference in magnitude. The original image was
created with an image of HD5980 and DAOPHOT used an image of SAO255763.
The contours are 0.001 (1), 0.003 (2),
0.01 (3), 0.03 (4), 0.1 (5), 0.3 (6), 1 (7) and 3 (8) magnitudes.
Note that the range in separation is not exactly the same as in the
previous figure
Figure 7 (click here) can be considered representative of the
performances of DAOPHOT in good conditions. It gives an estimate
of the best performance an adaptive optics system can achieve
when measuring the light of a faint companion next to a bright star.
The figure shows that a very good photometric accuracy (an error of
about 0.01) can only be achieved further than about 1 arcsec and
for a difference in magnitude not larger than 3 or 4.
Good photometric accuracy (an error between 0.01 and 0.1) can only be
achieved for a difference in magnitude less than 2 near the star,
and for a difference of 6 or 7 magnitudes further than 1 arcsec.
Only a poor accuracy (more than 0.1) is available near the main star
in most cases and, beyond 1 arcsec, for differences in magnitude larger
than 6 or 7.
When comparing the two figures, it can be noted that
the results are slightly better in the case of HD5980.
This is due to a longer exposure time (200 seconds instead of 6),
therefore smaller fluctuations in the halo, and also to a more careful
choice of calibration star. But note that
the two figures, even though they were
obtained in very different conditions and during different runs,
are nevertheless very similar, which indicates that they can
be considered typical and unlikely to be much improved in similar
atmospheric conditions.
We carried out a similar procedure using images of HD5980 and
SAO255763 obtained in the H-band. The integration times
were respectively 200 and 100 seconds, the Strehl ratios 0.13 and
0.15, the signal to noise ratios 5500 and 35000,
and the delay between the images 15 minutes.
Again the results were very similar, only slightly worse.
For a difference in magnitude of 2.5 between the main star and
its companion, the errors in the magnitude estimation were
respectively 0.15, 0.02 and 0.002 at 0.5, 1 and 2 arcsec,
compared to 0.15, 0.015 and 0.001 in the K band for the
same couple of objects. For a difference in magnitude of 5,
the errors were 0.6, 0.2 and 0.02 in H, compared to 0.6, 0.15
and 0.01 in K. This result confirms that only slight improvement
is obtained when the Strehl ratio is higher, at least in the
range 0.10 to 0.35. Better results could obviously be obtained for
higher Strehl ratios, say above 0.4.


Up: Photometry with adaptive
Copyright by the European Southern Observatory (ESO)

