Before applying our method to stellar interferograms obtained with the GI2T
interferometer, we have evaluated its performances on simulated data from
a numerical model for the GI2T+CP40. The model includes atmospheric disturbed
wavefronts, photon-noise and the PCH effect itself following the
operational mode of the GI2T described in Sect. 2.1.
In a first step, we produce phase disturbed wavefronts with a typical D/r0=10
characteristic of good atmospheric conditions at the Calern Observatory.
The wavefronts on the apertures are assumed uncorrelated (the baseline is larger
than the outer scale). From each wavefront we produce the continuous distribution
of intensity in the focal plane of the GI2T by computing the squared Fourier
transform of the complex amplitude on the pupil. We have to produce
these wavefronts at different wavelengths in order to simulate the spectrograph.
We produce monochromatic interferograms at different wavelengths for a given state
of turbulence. We select the central strip of these interferograms (one speckle wide)
that we reassemble in increasing wavelengths in order to simulate the dispersed
fringes over 100 Å (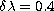
Å). Next we generate the
photon noise using this continuous distribution as the probability density
of photon arrival on the detector. We average the AC of these short
exposures for a typical number of 2000 different wavefront samples. We have
chosen to simulate the PCH by substracting a narrow 2D gaussian from the
center of the averaged AC. Thus by a Fourier transformation, we obtain
a biased power spectrum, which is taken as the starting step for removing the PCH (Fig. 2 (click here)).
We emphasize that the choice of a gaussian is just to mimic a PCH effect in the AC.
It does not influence the correction of the actual observations by GI2T on stellar sources.
Before the 2D polynomial fit of the noise background, we mask the low frequency and the
two high frequency peaks, but also the horizontal and diagonal spikes introduced by the
interferograms windowing (these spikes are shown in Figs. 2 (click here) and
3 (click here)). The horizontal spike is due to the spectral windowing.
The field windowing is done with an angle of 10 degrees which ensures that
the fringe peaks are not contaminated by the associated spike. The width of
the masks are fixed by the extent of low and high components in this
spectrum.
In order to determine the polynomial degree for the best fit, we can make the following
assumption based on the expected power spectrum. Knowing that the CC does
not suffer from the PCH, it is possible to estimate the fit quality
from the ratio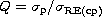 
. We compute therefore
the power spectrum and the cross-power spectrum corresponding respectively
to the spectral band 
and two spectral bands
, 
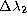. For a given image,
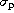and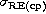 
are N and
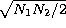respectively at high spatial frequencies. In order to
compare the standard deviations of power and cross-power spectra, one must
normalize 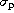by N2 and 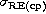by
N1N2. Hence:
Now the best fit is obtained according to two criteria: the average noise background
in the unbiased corrected power spectrum should be as close as possible to the theoretical
zero value. Second the final ratio Q should approach the theoretical value fixed by
N, N1 and N2. From Table 1 (click here), one can see that Q
converges rapidly for increasing polynomial degrees. For instance, it
stagnates at its theoretical value of 0.73 after the polynomial degree
has reached 5.
| polynome |  |  | Q |
| degree |  |  | |
| 3 | 1.266 | 5.1 | 0.75 |
| 4 | 1.244 | 3.2 | 0.74 |
| 5 | 1.243 | 3.5 | 0.73 |
| 6 | 1.243 | 4.0 | 0.73 |
| 7 | 1.243 | 1.9 | 0.73 |
and 
are the standard deviation and
the mean value of the photon noise in the power spectrum, expressed in
fractions of the total energy. The theoretical ratio Q is 0.73 according
to the number of photons in the different spectral windows
The next step for validating our approach is to apply the method to actual interferometric
data. As previously done on simulated spectra, we have analized the Q convergence versus
polynomial degree. From Table 2 (click here), one can see that it stagnates at
its predicted value of 0.77, fixed by the photon numbers in each spectral
window of 
Cep interferograms, after the polynomial degree has
reached 10. The need to iterate to high degrees comes from the
fact that the PCH artifact appears actually as
a more complex 2D distribution (Fig. 4 (click here)). For instance, and
depending on the average photon rate per pixel, it can exhibit positive
"ears'' (see Fig. 1 (click here) top) due to the CP40 centroiding hardware
electronics. These "ears'' create an additional modulation of spectral
densities that high order polynomial fits completly eliminate
(Fig. 3 (click here)).
Figure 3 (click here) illustrates the results of our method applied to a bright star
( Cep, V=2.4) and a faint star (P Cygni, V=4.8).
Figure 3: Results of the correction technique on actual GI2T observations.
The two top images display the biased and corrected power spectra of
Cep. These at the bottom display PCyg. The polynomial degree is 11.
The horizontal and vertical directions correspond respectively to the wave
number and to the angular frequency
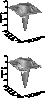
Figure 4: Fits of the PCH artifact computed from the Cep (top) and PCyg (bottom)
biased power spectra (coordinates are in arbitrary unit)
| polynome | | | Q |
| degree |  | | |
| 5 | 4.431 | 18 | 1.10 |
| 6 | 3.659 | 4.0 | 0.92 |
| 7 | 3.648 | 4.0 | 0.91 |
| 8 | 3.229 | 9.5 | 0.81 |
| 9 | 3.225 | 7.4 | 0.80 |
| 10 | 3.108 | 2.7 | 0.78 |
| 11 | 3.107 | 4.4 | 0.77 |
| 12 | 3.107 | 3.8 | 0.77 |
Cephei
on october 17th 1994. and are the
standard deviation and the mean value of the photon noise in the power
spectrum, expressed in fractions of the total energy. The theoretical ratio
Q is 0.77 according to the number of photons in the different spectral
windows
The visibilities obtained from the GI2T are determined by computing the
ratio of high to low frequency energies in the power spectrum. In theory
the support of the high-frequency components are defined by the AC of the
output pupil of the GI2T. In practice, the geometry of this ouput pupil is
subject to mis-alignment of the optics or telescopes guiding errors. Also,
optical path difference variations spread the high frequency energy accross
the wave number axis. Therefore, the high frequency support is not exactly
known. Until now, we have used the following criteria for determining the
fringe support: the points close to the cut-off frequency being at the
level of the photon noise, only the frequencies where the signal is twice
as large as the photon noise were taken into account. Thus the visibility
measurement is directly signal to noise dependent. With the present
correction where the PCH is removed, the high frequency peak can be
integrated on a support larger than its cut-off frequency without changing
the total energy. This is due to the fact that points outside this peak have
now a zero mean value.
Therefore, the estimate of the high frequency energy does not depend on
the exact extent of its support anymore. However its signal to noise ratio
is determined as the ratio between the high frequency energy
and an energy defined as the integration of the standard deviation of the noise
over a support corresponding to the high frequency peak.
This support, that is not necessary for the
visibility measurement itself, is determined by taking into account just the
points exceedings twice the standard deviation of the noise. The uncertainty
on a visibility measurement is defined as the following (M94b):
From Table 3 (click here), one sees that the effect of support variation in the wave number direction corresponds to visibility variations smaller than the error on the latter. The same result is obtained by growing the support in the angular frequency direction.
| support size | Visibility |
| (pixels) |  |
 |  |
 |  |
 |  |
 |  |
 | |
 |  |
. In the angular
frequency direction: 20 pixels correspond to 
. In our case,
nm, 
nm, D=1.5 m and S/N=13.8)Cep
In this paragraph, we demonstrate the improvement of visibility estimates
with our technique over previous data reduction methods (M94b, Mourard et
al. 1997). We use observations of Cep (night of October 16, 1994)
in the spectral band 669 to 675 nm near the HeI line. The 30 minutes of
observation are divided in sequences of 3 minutes. For each sequence, the
power spectrum is obtained by Fourier transforming the averaged AC of the
20 ms frames recorded by the CP40. Each short exposure contains 120 photons
on average. The power spectra are processed to remove the artifact due to
the PCH. Thus, the visibilities are derived from the unbiased power spectra.
The result is presented in Fig. 5 (click here).
From the set of individual visibility measurements, we calculate a nightly average and a standard
deviation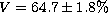 
. This standard deviation gives a good estimate for the error on the
visibility. The same work has been carried out (Mourard et al. 1997) by using the old PCH
correction method. The hole was filled in using polynomial interpolations along the central rows
of the AC (in the direction of dispersion). The obtained nightly average and standard
deviation were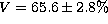 
. So, the relative error on the visibility has been reduced by about 1/3 by using
the new PCH correction.
Figure 5: Short-sequence visibility measurements for Cep on one night (S/N=14.0)