3. Element diffusion

A general discussion on the relevance of element diffusion in the evolution of Pop.II stars has been already given in a previous paper (Castellani et al. 1997: Paper II) and it will be not repeated here. Here we only recall that the diffusion of both He and heavy elements is taken into account, according to the algorithm adopted in Thoul et al. (1994).

 

Z M

(Gyr) (K)

0 . 0002 0 . 6 30 . 8 -0 . 078 3 . 751

0 . 0002 0 . 7 17 . 7 0 . 140 3 . 786

0 . 0002 0 . 8 10 . 9 0 . 330 3 . 814

0 . 0002 0 . 9 7 . 1 0 . 536 3 . 848

0 . 0002 1 . 0 4 . 9 0 . 702 3 . 890

0 . 001 0 . 7 18 . 7 0 . 026 3 . 770

0 . 001 0 . 8 10 . 9 0 . 187 3 . 794

0 . 001 0 . 9 6 . 7 0 . 348 3 . 818

0 . 001 1 . 0 4 . 8 0 . 551 3 . 847

0 . 006 0 . 65 35 . 1 -0 . 255 3 . 721

0 . 006 0 . 70 26 . 6 -0 . 172 3 . 733

0 . 006 0 . 80 15 . 4 -0 . 027 3 . 754

0 . 006 0 . 90 8 . 7 0 . 101 3 . 774

0 . 006 1 . 0 5 . 1 0 . 245 3 . 794

. . . . .

Table 6: Selected evolutionary quantities for models with diffusion at the track TO. The age at the track TO is in Gyr

 

Table 6 (click here) gives selected evolutionary properties of models for the various choices on the stellar mass and for the investigated metallicities. As a whole, our results closely follow the general trends discussed by Proffitt & VandenBerg (1991) in their pioneering paper to which we refer the reader. Figure 5 (click here) compares the run in the HR diagram of isochrones with and without element diffusion for a selected metallicity and for the labeled choices on the cluster age whereas Table 7 (click here) gives detailed information on the isochrone TO luminosity and effective temperature.

  
Figure 5: H burning isochrones for Y=0.23, Z=0.001 and for the labeled ages for the present models without and with element diffusion (upper and lower panel, respectively). The time interval between consecutive isochrones is 1 Gyr. Note that the standard isochrones are calculated until a luminosity lower than that of the helium flash

 

(Gyr) (K)

8 0.557 3.840 0.881

9 0.501 3.831 0.852

10 0.450 3.822 0.826

11 0.406 3.814 0.804

12 0.346 3.809 0.783

13 0.313 3.804 0.766

14 0.283 3.800 0.750

15 0.255 3.796 0.736

16 0.228 3.793 0.723

17 0.204 3.789 0.711

18 0.180 3.786 0.700

8 0.429 3.814 0.888

9 0.383 3.807 0.861

10 0.342 3.801 0.837

11 0.305 3.796 0.816

12 0.259 3.791 0.795

13 0.232 3.788 0.779

14 0.206 3.784 0.764

15 0.183 3.781 0.750

16 0.160 3.778 0.737

17 0.140 3.775 0.726

18 0.120 3.773 0.715

9.5 0.265 3.776 0.926

10 0.244 3.774 0.914

11 0.204 3.770 0.891

12 0.185 3.767 0.874

13 0.156 3.763 0.856

14 0.129 3.760 0.840

15 0.090 3.757 0.823

16 0.067 3.755 0.809

17 0.047 3.752 0.797

18 0.031 3.750 0.785

Table 7: Selected TO quantities for H burning isochrones with diffusion for the labeled assumptions about age and original chemical composition

 

Tables 6 (click here) and  7 (click here) correspond to Tables 2 (click here) and 3 given in the previous section for computations neglecting element diffusion. Figure 6 (click here) shows the dependence of (isochrones) TO luminosity on cluster age, as compared with similar results but without allowing for element sedimentation.

  
Figure 6: Dependence of the TO luminosity on the cluster ages for the three labeled metallicities. The results for canonical models (dashed line) are compared with similar results but for models with element sedimentation (solid line)

In the case of sedimentation the best fitting of the data connecting ages to TO luminosities gives the following relation for ages between 8 and 18 Gyr:
Log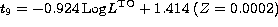
Log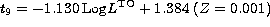
Log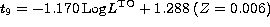

which again reproduce the results to within a few 10⁸ years.

According to the discussion given in Paper II for the case Z=0.0004, one finds that element diffusion moderately decreases theoretical expectations for TO luminosities for each given cluster age. Figure 6 (click here) now shows that such an effect depends on the assumed metallicity, increasing when the metallicity is decreased. As a matter of the fact, the effect of diffusion on the TO luminosity is larger in the most metal poor isochrones since the diffusion in the stellar envelopes is larger due to the thinner convective envelopes on MS stars. At the lowest metallicity 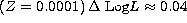: thus, for a given observed TO luminosity, allowing for sedimentation would decrease age estimates by about 10%. On the contrary, when Z=0.006 one expects negligible variations.

Table 8 (click here) gives selected structural parameters of models at the He flash, to be used as input to the He-burning models (for a discussion of the effects of diffusion on the luminosity of the RGB "bump", see also Cassisi et al. 1997).

 

0 . 7 0 . 5188 0 . 2144 20 . 33 3 . 359 2 . 056

0 . 8 0 . 5148 0 . 2261 12 . 77 3 . 352 2 . 139

0 . 9 0 . 5113 0 . 2344  8 . 51 3 . 344 2 . 209

1 . 0 0 . 5081 0 . 2402  5 . 96 3 . 334 2 . 290 Z=0.001

0 . 7 0 . 5107 0 . 2178 22 . 24 3 . 410 1 . 825

0 . 8 0 . 5068 0 . 2294 13 . 98 3 . 404 1 . 917

0 . 9 0 . 5041 0 . 2377  9 . 28 3 . 398 1 . 983

1 . 0 0 . 5018 0 . 2434  6 . 46 3 . 393 2 . 043 Z=0.006

0 . 7 0 . 5034 0 . 2184 31 . 36 3 . 460 1 . 399

0 . 8 0 . 5001 0 . 2308 19 . 91 3 . 457 1 . 495

0 . 9 0 . 4975 0 . 2392 13 . 30 3 . 457 1 . 578

1 . 0 0 . 4958 0 . 2446  9 . 20 3 . 530 1 . 657

. . . . . .

Table 8: Selected evolutionary quantities for stellar models with element diffusion at the He flash. The age at the He flash is in Gyr

 

On this basis we present in Fig. 7 (click here) a comparison between HB evolution with or without diffusion; in the same figure the path in the HR diagram of these models is also compared with similar results from CCP.

 

M LogL

(K) (Myr)

0.53 1.352 4.395 -

0.54 1.369 4.352 -

0.55 1.386 4.318 86.6

0.58 1.437 4.237 -

0.60 1.478 4.192 78.1

0.62 1.524 4.145 78.0

0.65 1.593 4.072 76.0

0.70 1.678 3.952 73.9

0.72 1.703 3.909 -

0.75 1.734 3.849 72.9

0.77 1.751 3.813 -

0.80 1.773 3.772 66.6

M LogL

(K) (Myr)

0.53 1.337 4.343 95.0

0.55 1.376 4.263 92.8

0.60 1.540 4.095 84.8

0.65 1.671 3.866 81.4

0.70 1.730 3.735 80.3

0.75 1.760 3.719 78.7

Table 9: Selected evolutionary quantities for HB models with diffusion. The time spent during the central He burning phase is in Myr

 

Table 9 (click here) gives details on the ZAHB structures and on the corresponding helium burning evolutionary times. HB structures presented in both Fig. 7 (click here) and Table 9 (click here) assume a 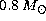model as H-burning progenitor. However, Table 8 (click here) shows that, e.g., increasing the RG masses (thus decreasing the cluster age) 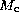decreases but increases, with balancing effects on the predicted HB luminosities. As a result, numerical experiments disclose that HB data based on a 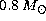progenitor can be safely taken as representative of HB models in the range 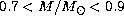, at least, thus covering quite a large range of cluster ages.

  
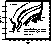
Figure 7: Comparison of the HB evolution for models with (solid line) and without (dashed line) diffusion for Z=0.001 and Y=0.23. Similar results from CCP (dot-dashed line) are also shown

  
Figure 8: TO luminosities for selected labeled ages and ZAHB luminosities at 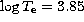as a function of metallicity, for models with (solid line) and without (dashed line) element diffusion

Figure 8 (click here) summarizes the results of this paper concerning cluster ages, showing the run with metallicities of ZAHB and TO luminosities, with or without diffusion, and for selected choices about the assumed ages. In this figure, data concerning the TO luminosity have been supplemented with similar data but for Z=0.0004, as given in Paper II with a "step 4" physics which is fully compatible with present computation as far as central H burning models are concerned. As already discussed, present HB are brighter than estimated in Paper II (see Table 1 (click here)). However, the same Fig. 8 (click here) shows that present computations keep predicting that diffusion decreases the HB luminosity by about , in agreement with the results of Paper II.

  
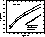
Figure 9: The calibration of age in terms of the difference in luminosities (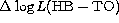) between ZAHB (at 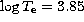) and TO, as predicted by present models with (solid line) and without diffusion (dashed line) and Z=0.0002. The results are compared with original predictions by CCP (dotted line)

Figure 9 (click here) shows the calibration of age in terms of the difference in luminosities between ZAHB (taken at 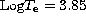) and TO, as predicted with or without diffusion, and as compared with original predictions in CCP. As discussed in Paper II one finds that diffusion plays a minor role in that calibration. However, the same Fig. 9 (click here) shows that the new physics, as a whole, reduces by about 4 Gyr theoretical calibrations based on the old physics.

The detailed comparison between theory and observation is a delicate question, beyond the scope of this theoretical paper. However, one may test present predictions by comparing with recent estimates of HB luminosities derived by recent Hipparcos parallaxes measurements. This is shown in Fig. 10 (click here), which compares the data presented by De Boer et al. (1997) with our theoretical predictions converted in M_v, B-V magnitudes according to model atmospheres by Kurucz (1992). One finds that the HB luminosity level appears in quite good agreement with the quoted observations. Here we only notice that the two stars which lie below the ZAHB around both have been corrected for a rather large reddening (E(B-V)=0.10), one -to our knowledge- devoid of recent metallicity estimates.

  
Figure 10: a) Theoretical ZAHB for standard models compared with Hipparcos estimates of HB magnitudes from De Boer et al. 1997 (see text). When available, labeled metallicities are from Gray et al. 1996. b) As a) but for models computed by accounting for element diffusion

  
Figure 11: The dependence on metallicity of the difference in luminosities between ZAHB (at 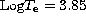) and TO (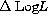(HB-TO)), as predicted by present models with (solid line) or without diffusion (dashed line) for selected labeled ages. Present results are compared with original predictions in CCP (dotted line)

As for the outcome of the improved theoretical scenario, let us recall that in Paper I it has been already shown that in the step 4 scenario the color magnitude diagram of a typical metal poor galactic globular can be reproduced by a 12 Gyr (no diffusion) isochrone. Taking into account that, at 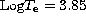, our best HB models without diffusion turn out to be more luminous by , one estimates that the "new" age shifts toward 11 Gyr without sedimentation, and even lower if sedimentation is taken into account.

Figure 11 (click here) shows that present results give a rather low dependence of 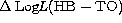on the cluster metallicity. As a matter of the fact, assuming, e.g. an age of 12 Gyr one finds that passing from Z=0.0002 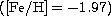to Z=0.001 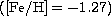we predict an increase in 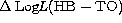corresponding to 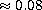mag, independent of any assumptions about the efficiency of sedimentation; this difference increases when the cluster age is decreased.