The fact that the slopes in Fig. 5 (click here) are different for Saharan dust
and for non-Saharan dust episodes means that the aerosol particles have at
least different size distributions. Using Mie theory, the extinction
coefficient may be defined as
where 
is the extinction efficiency factor,
n(r) the particle size distribution in the atmospheric column, r the
particle radius, m the particle refractive index, and 
the
wavelength of the incident light.We computed the extinction efficiency factors
for the wavelengths used in this work using the Mie scattering code of
Wiscombe (1980) and obtained Fig. 6 (click here). The difference
between the extinction efficiency factors at two different wavelengths is
just a shift in particle sizes as shown in Fig. 6 (click here)a. There is a
particle radius for which the efficiency factors have reached the value of 2
at all wavelengths. Particles with this and larger radii contribute to the
extinction coefficient in the same quantity regardless of the wavelength.
The radius interval where the extinction coefficients vary with wavelength
can be determined by applying the criterion of Heintzenberg et al.
(1981), who represented the ratios of the extinction efficiency
factors at different wavelengths as a function of particle radius. Then, the
extinction coefficients are wavelength dependent (slopes different from
unity) if the aerosol particle sizes are in the radial interval where these
ratios are not constant. Also, the extinction coefficient is not wavelength
dependent (slopes equal to unity) if the aerosol particle sizes are outside
that interval and consequently the ratios are constant. Note that the
dependence on wavelength is an effect of the independent information
content in a set of multi-wavelength optical data. Figure 6 (click here)b shows
the criterion of Heintzenberg et al. (1981) applied to the
wavelengths 450, 770 and 870 nm, for the complex refractive index of
1.55-0.005i (
). Fouquart et al. (1987),
Carlson & Benjamin (1980), and Patterson (1977)
considered this refractive index for Saharan dust aerosols. From
Fig. 6 (click here)b, the particles with sizes around 100 nm, lead to extinction
coefficients that show wavelength dependence.
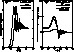
Figure 6: a) Extinction efficiency factors at 450 and 870 nm for a
refractive index of 1.55 - 0.005i. Note that both curves are exactly the
same except for one being shifted from the other. b) Ratios of
extinction efficiency factors for selecting the interval of radius where the
extinction coefficients can show wavelength dependence
This section shows that the extinction coefficient wavelength dependence is in good agreement with the criterion of Heintzenberg et al. (1981). Both Saharan and non- Saharan aerosol conditions are simulated to show how dust particles cause the non-wavelength dependency. Atmospheric aerosol size distributions are characterized by a multi-modal model, and each mode is represented by a lognormal distribution. We will consider the following three modes: (1) the "accumulation mode'' with the smallest particle sizes, (2) the "coarse mode'' with larger sizes than the accumulation mode, and (3) the "dust mode'' with the largest sizes. Aerosol size distributions have not been measured at Teide Observatory on a long-term basis, but Saharan dust optical properties and size distributions have been studied in many African locations in recent years. D'almeida (1987) measured the size distribution in Timbuctu and in Agadez for three different weather regimes: 1. "desert background'', when aerosols are present at a relative low concentration for the site; 2. "desert with wind carrying dust'', when some dust aerosol particles are transported from the desert and added to the background aerosols, and 3. "sand storm'', high concentrations of dust particles come directly from the desert. Trimodal lognormal size distributions were then fitted to the measured data. Obviously, the size distribution measured during a sand storm is not representative of Teide Observatory aerosol size distributions because most of the larger particles are not transported very far. Therefore, we assumed only the "desert background'' and the "desert with wind carrying dust'' size distributions to calculate approximate values of the extinction coefficients for Saharan dust episodes at Teide Observatory. The third mode was used in the study for further clarification. The refractive index assumed in this case was 1.55-0.005i.
To represent a non-Saharan episode, we assumed size distributions from Whitby (1978), which are derived from averages of measurements on sites of the same category. We chose the categories representative of "clear day background'' and "polluted clear days''. We assumed a refractive index of 1.45, which is representative of sulphuric acid components (Palmer & Williams 1975) at 20% relative humidity (Charlson 1978). This relative humidity is in the interval of relative humidities measured at Teide Observatory. A layer 1 km thick was considered in both cases. The other atmospheric layers were considered to contribute to the extinction coefficients similarly in both conditions, with and without Saharan dust. We seek particle sizes that affect the extinction coefficient dependency with wavelength and consider only spherical particles using Mie theory. Figure 7 (click here)a shows these four size distributions and Fig. 7 (click here)b the corresponding extinction coefficients computed using the distributions of Fig. 7 (click here)a. In Fig. 7 (click here)b we have also included two more results obtained for Saharan dust episodes but using only the "accumulation mode'': "accumulation mode of desert with wind carrying dust'' and "accumulation mode of desert background''. Also to estimate the influence of the "dust mode'', we calculated the extinction coefficient for Saharan dust episodes but only for the accumulation and coarse modes (not plotted in Fig. 7 (click here)b) concluding that the third mode contribution ("dust mode'') to the extinction coefficients was only of about 1%. Also extinction coefficients calculated considering both the whole size distribution and only the accumulation and coarse mode, were not wavelength dependent for Saharan dust episodes, and the extinction coefficients calculated for just the accumulation mode of the size distribution showed wavelength dependence. On the other hand, the extinction coefficients calculated for the Whitby size distributions ("clear day background'') showed wavelength dependence either way, considering the whole size distribution and only the accumulation mode. It can also be concluded from Fig. 7 (click here) that: (1) The aerosol particles in the first mode of all the size distributions considered (Fig. 7 (click here)a), yield extinction coefficients that are dependent on wavelength. The radius range containing the independent information in the wavelengths is around 100 nm. But since the efficiency factors of particles with radii smaller than 20 nm is close to zero (see Fig. 6a), their contribution to the extinction coefficient is negligible. Therefore, these smallest sizes of the accumulation mode do not make any difference to the slopes of Fig. 5. (2) The large number of particles with radii over 2000 nm approximately, with large volume, makes the extinction coefficients independent of wavelength in the Saharan dust cases. (3) In the non-Saharan dust cases, the small number of particles with radius larger than 2000 nm is not enough to make the extinction coefficients independent of wavelength. Hence, only the particles with a radius of about 100 nm lead to the wavelength dependence of the extinction coefficients, as was concluded from the criterion of Heintzenberg et al. (1981).
Figure 7: a) Known aerosol size distribution in different conditions
taken from the
literature and used in this article. b) Extinction coefficients
computed using Mie theory for the whole size distribution of a) and
in two cases only for the accumulation mode (see text)
Before obtaining the aerosol size distribution from the measured extinction coefficient at Teide Observatory, we introduce the limitations of the method.
Aerosol size distributions can be obtained from inversion of multi-wavelength
extinction coefficients (i.e. inversion of Eq. (1)) using the inversion
algorithm of King et al. (1978). However, the inversion
problem is ill-posed and there are many solutions that reproduce the input
data with an error smaller than 0.1%. The assumptions needed in the
inversion are the assumptions of Mie theory that considers spherical
particles, the aerosol composition through the refractive index, and the
radius range for which, the spectral optical depths contain independent
information of the particle sizes. These assumptions lead to many
uncertainties in the inversion solutions (Gonzalez Jorge & Ogren
1996). (1) Dust aerosols are rarely spherical particles,
Heintzenberg (1978) concluded that applying Mie theory to
non-spherical particles systematically distorts the size distribution
leading to a shift in the concentration maximum to smaller sizes. (2) The
assumptions of a wrong refractive index slightly alter the shape of the
retrieved size distribution. In this case, the maximum of the retrieved
size distribution modes decreases as the assumed real part of the refractive
index increases with respect to the real one. Depending on the assumed
refractive index, 1.45 or 1.55-0.005i, the retrieved modes have more or
fewer particles, respectively. (3) To obtain the size distribution with the
inversion method, a finite size range is required. We chose the range
between 20 and 3000 nm because it covers the largest possible size range in
which particles can lead to extinction coefficients with wavelength
dependence. This finite size range ignores the contribution of the larger
particles to the extinction coefficients. As a consequence, extra particles
may be placed around 3000 nm. Also, extra particles may appear around the
minimum between two retrieved modes or around 20 nm. To increase the
selected size range the wavelength interval needs to be extended (1) to the
UV to retrieve smaller sizes, and (2) to the IR to retrieve larger
particles. The finite size range may lead to errors of about 80%, 30% and
30% in the retrieved total number of particles
, total surface area 
, and total volume
, respectively
(Gonzalez Jorge & Ogren 1996). The large error in the total
number of particles is due to the size distribution truncation for sizes
smaller than 20 nm. Since these particles contribute little to the total
surface area and the total volume, not including them in the retrievals
yields smaller errors in the retrieved total surface area and total volume
than in the retrieved total number concentration of particles. For this
reason we will represent the retrieved aerosol size distributions measured
at Teide Observatory as volume size distribution (i.e., total volume of
particles at each radius range 
).
For the purpose of this section we need to select the extinction coefficient values to be inverted. One of the more important parameters for the inversion is the number of different wavelengths simultaneously available. As explained in Sect. 2, the aim of the observational campaign was not this kind of study but helioseismology. Because to this, the set of filters was changed several times during the whole campaign. The five wavelengths we are using in this work were never simultaneous, only two by two or three by three and at different periods. Since the inversion algorithm gives better results using more than three wavelengths, we have created the extinction coefficients based on the straight-line fit of Fig. 5 (click here) (Table 3 (click here)) to the real data. To compute the extinction coefficients for "clear days'', we use the straight lines of Fig. 5 (click here)a, we select extinction values for 680 nm from 0.01 to 0.06 in steps of 0.01 and compute the corresponding to the other four wavelengths using the straight lines. For "dust'' episodes we do the same but using the straight lines of Fig. 5 (click here)b and choosing the extinction values for 680 nm from 0.1 to 0.8 with steps of 0.1.
For the inversions we assumed the size range from 20 nm to 3000 nm, and the refractive indices 1.55 - 0.005i and 1.45 for Saharan and non-Saharan episodes, respectively. Figure 8 (click here) shows the result for "clear days'' and Fig. 9 (click here) for "dust'' episodes. Note in Fig. 8 (click here) how the maximum of the accumulation mode volume for particles with radii below 80 nm decreases as the extinction coefficient increases, whereas it stays approximately constant for particles with radii between 80 and 100 nm. For particles larger than 100 nm the volume increases, these particles being responsible for the increase of the extinction coefficient even when their volume is not too high because the extinction efficiency factor increases very rapidly over this range of radii (Fig. 6 (click here)a). In Fig. 9 (click here) the maximum of the coarse-mode volume increases with increasing extinction coefficients for Saharan dust episodes. Clearly, size distributions retrieved from extinction coefficients during Saharan dust have larger volume concentration at the coarse sizes than size distributions during other situations, as expected from the extinction coefficient wavelength dependence. The fact that all the changes in the coarse mode with increasing extinction coefficient are increases in the volume maximum and not shifts of the mode to larger sizes can be a result of using a size range limited from 20 to 3000 nm and the extinction coefficients computed from the straight-line fits. This last is an effect of constraining all the extinction coefficients to have exactly the same wavelength dependence, which means constraining the retrievals to vary the number of particles but not their sizes. It should not be ignored that the extinction coefficients are not exactly on the fitted lines, and a change in the extinction coefficients could be explained also as a shift of the coarse-mode maximum to larger sizes.
From the retrieved size distributions for K680= 0.06 (Fig. 8 (click here)) and K680= 0.1 (Fig. 9 (click here)) it might be inferred that the transition between no dust and dust episodes is straightforward. However, the retrieved size distributions assuming the refractive index of 1.55-0.005i for K680= 0.09 (Saharan dust conditions) had less coarse particles than the retrieved size distributions assuming 1.45 for K680 = 0.07 (non-Saharan dust conditions). This discrepancy was related to the refractive index assumption. The change in the aerosol composition during the dust invasion is gradual as is the change in the extinction coefficient. Therefore, it would be more appropriate to assume a combination of the two models, suggesting that aerosol size distributions and compositions of both conditions may be mixed in the transition from non-Saharan dust to Saharan dust episodes. Even though we chose refractive indices according to the literature, there is still work to be done on aerosol refractive indices. However, a wrong assumption of the refractive index in the models would only yield a systematic increase or decrease in the maximum of the size distribution modes and would not alter the general trend.
Figure 8: Aerosol volume size distributions retrieved from the extinction
coefficients at Teide Observatory for non-Saharan dust episodes
(clear days). The input data were obtained from the linear fits to the real data
(Fig. 5 (click here)a). See text
Figure 9: Aerosol volume size distributions retrieved from the extinction
coefficients at Teide Observatory for Saharan dust episodes
(dusty days). The input data were obtained from the linear fits to the real data
(Fig. 5 (click here)b). See text