The basic problem
of the conical scan technique is how to retrieve the
pointing errors, i.e. the best estimates of the two numbers 
and 
.
One possibility is given by the
simple fact that as conical scanning operates by displacing the
antenna beam to successive positions, it is possible to measure
the difference in the relative signal strength, expressed by
. The signal difference,
, is a function of the angular difference, 
,
and as we shall see below it can be used to calculate the pointing errors.
However, we shall first review the standard method, consisting of recording
the antenna signal and computing sums weighted by sine and cosine factors.
We then discuss two analytical methods which exploit
the measurement of the signal difference. In each case, we assume
that a total of N measurements are taken in one 
scan,
at intervals, each one lasting 
seconds.
We also note that the standard method, as discussed below,
assumes that 
is
known at the time of the pointing measurement. This may not always be
the case, especially if the pointing source is variable
and has not been observed for a long time. The two successive
analytical methods, however, do not need the knowledge of .
This can be an important advantage when the flux density of the pointing
source is poorly known a priori. However, we shall show that an
inaccurate at most leads to over- or underestimates in the
amplitude of the pointing error, 
, but still accurately
estimates the ratio 
, i.e. the direction towards the source.
is unimportant for small , and hence a sequence of scans
converges rapidly.
The standard method consists of directly fitting the antenna signal
using Eq. (6 (click here)). The target position 
provides the
variables and the best-fit model is found minimising the value of
. When this method is used without further simplifying
Eq. (6 (click here)), it is much slower than fitting the signal difference or
using the dot-product technique, which we discuss below. However, the
antenna signal is much less noisy than the signal difference and, being a
numerical method, we can use any beam shape to fit the data, and not just
a Gaussian beam as it is assumed in Eq. (6 (click here)).
The standard fitting method is very simple in those cases where Eq. (6 (click here)) can be linearized, and a much quicker least-square fit technique can be used, making this method more useful in all practical cases.
As 
and are constants, only the right-hand side
exponential in Eq. (6 (click here)) is time variable, for 
.
Expanding this factor to first order:
or, using an angle 
to define the unknown
direction of the pointing offset , such that
then, Eq. (7 (click here)) can also be written as:
We then see that the expansion to first order
made in Eq. (7 (click here)) is
valid when 
, i.e. 
and
for 
and 
, respectively
(for the case 
see below).
Solution of Eq. (7 (click here)) for and is straightforward;
in fact, multiplication by 
and 
, and then
integrating with respect to
between 0 and 
exactly cancels the constant and the
orthogonal (
) terms, leaving:
where we have defined:
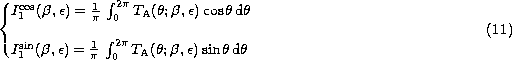
and 
are recognizable as the first sine and cosine
term of the Fourier series of 
. We give further
details in Appendix A, where
we also discuss the case of an elliptical
antenna beam, and the useful information that can be obtained utilizing
the Fourier series.
Equations (10 (click here)) are the analytic least square fits to and
in the linearized Eq. (7 (click here)), and make the standard fitting
technique an analytical method similar to those
discussed in Sect. 3.2 (click here).
We note that Eqs. (10 (click here))
contain 
on their right-hand side, which is unknown.
In the assumption of small pointing errors
this is not a concern. However, the angular
direction of the pointing offset, , can be
obtained with no approximations
by taking the ratio of Eqs. (10 (click here)) and using
Eqs. (8 (click here)):
Also, this result is completely general. If the ratio of
Eqs. (11 (click here)) is taken with being
given by Eq. (6 (click here)), rather than Eq. (7 (click here)), it can be
easily shown that 
.
Once the direction of the pointing offset is known, we can then solve
Eqs. (10 (click here)) for using its definition,
:
which can be numerically solved for if one can discriminate
between the double-valued solution.
One method is to use an initial ON-OFF measurement. This is a
sensitive estimate if is large, compared to the values
leading to the approximation contained in Eq. (7 (click here)),
which cannot be used in this case. From Eq. (6 (click here)) for
, the ratio of measured to expected antenna temperature is:
and it is thus straightforward to obtain:
For 
the pointing error is larger than 1/4 beamwidth. In such
cases the approximation used in Eq. (7 (click here)), which leads
to Eq. (13 (click here)), is not as
good as that from Eq. (15 (click here)). However, the value of
calculated by Eq. (12 (click here)) is totally
independent of the approximation used in Eq. (7 (click here)), as
stated above, provided that the beam is Gaussian.
The telescope pointing direction should be changed using
and the estimate of from Eq. (15 (click here)), until the
pointing error is less than 1/4 beamwidth. Once 
Eq. (13 (click here))
can be used . This estimate is more sensitive for small
than Eq. (15 (click here)), and is not subject to baseline errors, as it
uses only the variation of 
during the conical scan, rather than
its mean value. Hence, applying a sequence of pointing corrections will move the
telescope in such a direction as to reduce the offset.
If 
the error is larger than 1 beamwidth. Such a result should
be flagged to the telescope operator,
as it may be the result of radio frequency
interference (RFI) or an incorrect source position.
In Fig. 2 (click here) we show the difference between the least-squares solutions
and the approximation given by the use of
Eq. (7 (click here)), for various values of and for 
.
We note that the maximum peak-to-peak amplitude in the response is obtained when
. In fact, the exact value for the conical
scan radius corresponding to the maximum peak-to-peak
amplitude is expected to be from Eq. (9 (click here)) equal to
. Given the
relatively low value of 
in Fig. 2 (click here) (see also
the top panel of Fig. 5 (click here)), the fits
representing the results of the linearized standard method (dashed lines)
lie reasonably close to those obtained by minimising a (solid lines),
but in each case the linearized method underestimates the true error.
One potential pitfall of the conical scan method arises from the absence of any modulation for perfect pointing, which could be confused with total absence of the pointing source or some other breakdown in the system. However, an intentional offset of the boresight position by a small fraction of a beamwidth can provide a known modulation amplitude to prove that the system is functional.
Figure 2: Comparison between the fit to the antenna signal (points)
utilising the linearized standard method (different types of
dashed lines) and the fit (solid lines). The pointing error
is fixed (, or ,
in FWHM units) and we consider three different
values of , the radius of the scan, in FWHM units: 0.2 (filled
triangles and short-dashed line), 0.4
(filled squares and dotted line), and 0.6 (filled circles and
long-dashed line). The data shown are for 
s,
and a 
(we have also
assumed that the detection bandiwdth is 
MHz and the
system temperature 
K)
When is taken small enough (
),
then can be approximated using Taylor's expansion to first order
and Eq. (6 (click here)):
If we now define a normalised signal difference
,
one finally gets:
can be a very noisy signal, because of the operations
involved: the difference between two signals close in
intensity, and the division by the signal itself, 
which,
depending on the relative position of the source with respect to the center
of the beam, can be very close to the noise level in
some parts of the scanning circle.
Equation (17 (click here)) can be compared with the measured signal difference,
and because of its simple mathematical form it can be fit with a quick
generalised linear least square technique, without having to numerically
minimise a -value, as we explained in Sect. 3.1 (click here).
The results are discussed later in Sect. 4.1.2 (click here).
An important consequence of normalising the signal difference is that
Eq. (17 (click here)) is independent of the absolute flux density of the
pointing source. Therefore, as we mentioned earlier in this section,
the fitting method and the successive dot-product method are not
affected by the (poorly known) values of . Equation (17 (click here)) is
also independent of , although the resulting signal-to-noise
ratio (SNR) will depend on the radius of the conical scan, as is shown
in Fig. 4 (click here).
This method still
assumes a Gaussian beam shape, although this is generally not the case.
The angle-error estimate can be accomplished by the hardware,
using a pair of phase-sensitive
detectors with a reference input from the scan system.
The phase detectors perform
essentially as dot-product (DP, hereafter) devices with sine-wave
reference signals at the frequency
of scan and of proper phase to obtain the
two numbers and . This can be
easily seen analytically by multiplying the normalized
signal difference by a sine-wave, 
, obtaining:
where 
is an instrumental phase factor.
By filtering out the two oscillating
components in the previous expression (see Sect. 4.1.3 (click here))
one is left with:
which gives and for 
and
, respectively; c
is a numerical factor depending on the filtering process (see
Sect. 4.1.3 (click here)).