2. The instrumental profile

2.1. Parasitic light

As is well known, the transmission of light through a Fabry-Perot interferometer is given by the Airy function:

where R is the coating reflectance, t the spacing between the plates, the refractive index of the material between the plates (air in our case), the angle of incidence, and the wavelength of the incident light.

For fixed , t and , the transmitted light consists of a series of narrow peaks (orders), the separation of which in wavelength is the Free Spectral Range (FSR), and for small :

Let us suppose that the interferometer plates are perfectly flat and parallel (t constant), and that the interferometer is illuminated by a perfectly collimated raybundle, normally incident on the plates (). In this case, the Full Width at Half Maximum (FWHM) of each order of the FPI only depends on the reflectance, and with sufficient accuracy, for R greater than about 0.85, it is:

Due to the periodicity of its passband, an FPI obviously demands a prefilter to be used as a spectroscopic device. In the case of an emission spectrum, with well spaced lines, an interference filter may be sufficient, but in the case of an absorption spectrum, like the solar one, a single order of the interferometer must be isolated. For this reason, the passband of the order sorter must be narrower than the interferometer FSR, which in turn, through Eqs. (2) and (3), depends on the required FWHM of the transmission order. If the use of the FPI is not limited to the strongest solar lines, the isolated order must be significatively narrower than a typical photospheric line, with a FWHM 100 200 mÅ. If we impose 20 mÅ, corresponding to a spectral resolution 300000, a FSR 1 Å is obtained for the interferometer. An order sorter with a FWHM 1 Å will be therefore necessary.

As described in Paper I, on the IPM a Universal Birefringent Filter is used as order sorter for the FPI. Each passband of the UBF has a shape which resembles a sinc² function, with a FWHM = 0.250 Å and a FSR = 128 Å at H. An interference filter (IF), with a FWHM 50 Å, is then sufficient to isolate a single UBF passband.

From the spectroscopic point of view, the instrument therefore consists of three filters mounted in series. If , and respectively are the IF, UBF and FPI spectral transmissions, the overall instrumental profile ) is:

When the maximum of the UBF transmission profile coincides with one of the FPI orders, it follows that the overall instrumental profile consists of one main peak and some side lobes. These unwanted transmission bands contribute to the parasitic light, defined as:

where and respectively are the wavelength of the transmission peak and of the first zero of the UBF passband.

As shown in Paper I, the parasitic light can be minimized by a suitable matching of the interferometer FSR with the spacing of the UBF zeroes. However, it must be taken into account that, decreasing the operating wavelength, the relative wavelength position of the UBF passband zeroes shrinks with respect to the maxima of the FPI transmission orders. For extended operating wavelength ranges, this therefore prevents the minimization of the parasitic light contribution from the UBF side lobes, that is obtained by adjusting the adjacent orders of the FPI on the first zeroes of the UBF passband. A realistic compromise is obtained by choosing an interferometer with a 3 mm plate separation. In this case, the side orders of the FPI coincide with the third zeroes of the UBF passband at H (FSR = 0.75 Å). The parasitic light is minimum ( 0.7%) at 6563 Å, and maximum ( 2.2%) at the blue edge of the useful wavelength range (4600 Å).

In practice, however, the aforesaid suppression of the unwanted orders of the interferometer is not secured if the UBF passband sensibly differs from the theoretical one and/or the tuning between the UBF and the FPI is not correct. These conditions therefore require a very careful research of the tune solutions for the nine crystal groups forming the UBF (see Paper I), and a wavelength stability of the UBF and of the FPI such as to secure variations of the parasitic light and of the overall passband transparency smaller than the required photometric precision (1%).

For a relative detuning of 9 mÅ at 5500 Å, the peak transparency of the instrumental profile decreases of 1%, while the parasitic light increases of 0.4%. As the interferometer is very stable in wavelength (see Sect. 2.3), this result requires a wavelength stability of the UBF better than about 10 mÅ. This is obtained by measuring the resistance of a platinum wire, wound on the crystal groups, and by applying small corrections to the angular position of each group. The drifts of the UBF passband can then be compensated, securing a wavelength stability of 1 mÅ, better than required.

2.2. Spectral resolution

As shown in Sect. 2.1, to reduce the parasitic light, a maximum plate separation of 3 mm must be adopted for the interferometer. This condition imposes a lower limit to the FWHM of the instrumental profile (Eq. (3)), lowering therefore the attainable spectral resolution. In particular, for a coating reflectance R = 0.95 (see Table 1 (click here)):

Although the reflective resolution is much larger than the demanded one ( 300000), we have to consider that in practice, if the raybundle associated with a given image point contains a range of values and/or covers an area of the FPI plates where, due to flatness errors, the plate separation t fluctuates, the transmission profile will be broadened with respect to the reflective one (see later). To evaluate the effective spectral resolution, we have therefore to consider the geometry of the rays incident on the interferometer plates.

 

Manufacturer Queensgate Instruments Ltd.

Type Mod. ET50 piezo-scanned and capacity servo-controlled

Clear aperture 50 mm

Plate separation 3 mm

Wedge angle 15'

Coating Multilayer broadband Wavelength range

Reflectivity 0.95 at 5500 Å Flatness errors of

each plate at 5461 Å after coating

Cavity tuning 2000 nm

Resolution 12 bits Settling time (response to step input) Temperature sensitivity of the interferometer Temperature sensitivity of the CS100 controller

Electronic noise equivalent 10 pm Hz^-1/2 rms displacement of interferometer plates with CS100

 

Two different optical mountings can be adopted. In the case of the so called classical mounting, the image formed by the telescope is collimated and the FPI is placed near the image of the entrance pupil. Each image point is then formed by a camera lens, which focuses a beam of rays propagating through the interferometer at the same angle with respect to the optical axis. In this case, the FWHM of each order of the FPI is larger than the reflective one (). In fact, the raybundle associated with each image point covers an area of the FPI plates within which the plate separation t fluctuates; for = 0, this is accounted for by the term in the following equation:

where p are the flatness errors (defects) in fractions of .

Moreover, for what concerns the off-axis image points, the largest effect is a shift of the transmission orders towards the blue (), following the well known equation:

In classical mounting, therefore, the final image plane is spectrally dishomogeneous, in the sense that the wavelength of each order is not the same on each point, but depends on its distance from the optical axis, and this is also true for a perfect interferometer.

Instead, in the case of the so called telecentric mounting, the entrance pupil is collimated and the FPI is placed near an image plane. Consequently, all the image points are formed by ray cones normally incident on the interferometer and containing all the possible directions allowed by the optics. In this case, the FWHM of each order of the FPI is larger than the reflective one, because the raybundle corresponding to each image point contains a range of values. Moreover, as the plate separation is not infinitely small, the ray cones always cover a small, but finite area of the FPI plates, and therefore, on each point of the final image plane, the FWHM of each order is also broadened by small scale flatness fluctuations.

In practice, to avoid that the interferometer plates are focused on the final image, the FPI is not placed on the image plane, but as far away as possible from it. In this case, each ray cone corresponding to each image point covers an area of the interferometer plates, the size of which depends on the distance of the FPI from the image and on the relative aperture of the beam. As the beam incident on the interferometer has a very small aperture (see later), the area covered by each ray cone is only some millimeter in size.

In conclusion, the FWHM () of the interferometer orders will be broadened by the flatness errors as well as by the varying , accounted for by the and terms respectively on the following equation:

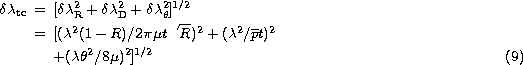
where are the small scale flatness errors in fractions of .

Generally p is defined as twice the maximum deviation of the considered surface from its ideal mathematical reference surface; this parameter combines therefore coarse and fine shape errors. However, in telecentric mounting, the broadening of the instrumental profile on each point of the final focal plane is produced by flatness errors, the scale of which is significatively smaller than the area of the interferometer plates. For this reason in Eq. (9) instead of p, has been used, which, as previously said, just represents the surface fluctuations at small scale. Since obviously , the term in is generally smaller than the corresponding one in ; in other words, the broadening of the instrumental profile produced by flatness errors is generally larger in classical than in telecentric mounting.

Also in the case of telecentric mounting, the final image plane is spectrally dishomogeneous, but in the sense that the wavelength position and the FWHM of each order randomly changes from a point to an other, due to the t fluctuations. However, unlike the case of the classic mounting, this is true only for a real interferometer.

Between the two optical mountings, the telecentric one has been adopted for the IPM. In this case it is possible to minimize the spectral dishomogeneities of the final image plane and to contain the broadening of the instrumental profile, produced by the varying , within the limit imposed by the demanded spectral resolution. As a matter of fact, for the adopted interferometer (see Table 1 (click here)), a surface accuracy of /150 after coating at 5461 Å is claimed by the manufacturer. As a consequence, the maximum wavelength fluctuation of the instrumental profile on the final image plane is 13.3 mÅ peak to peak (728 ms^-1) at 5500 Å. Moreover, assuming , , R = 0.95, and imposing a spectral resolution at 5500 Å, we obtain from Eq. (9) , i.e. an f/190 relative aperture of the beam incident on the interferometer. In classic mounting, instead, an exceedingly small relative aperture (f/820) should be used to have the same wavelength variation from the center to the edge of the field (Eq. (8)). In practice, an f/192 relative aperture has been adopted, corresponding to .

Assuming = 5500 Å, = 1, , R = 0.95, , (see Table 1 (click here)), we find:

where the inequality symbol is due to the assumption .

Following Eq. (9), we may conclude therefore that the FWHM of the instrumental profile and the spectral resolution of the IPM are:

2.3. Wavelength stability

As the overall instrumental profile essentially is one order of the interferometer, its wavelength stability essentially depends on the interferometer itself, and, in particular, on the stability of the optical length of the cavity, i.e. the product between the geometrical distance of the plates and the refractive index of the air between them.

On the adopted interferometer, the plate separation, as well their parallelism, are stabilized by a capacitance servo-control. A three channel bridge system, the CS100, uses capacitance micrometers to derive error signals when the spacing or the parallelism change. These signals are then used to drive piezo-electric staks which move to correct the errors. Because this is a close-loop system, non-linearity and hysteresis in the piezo-electric are entirely removed.

The CS100 however can erroneously adjust the geometrical distance of the plates, thus producing wavelength instabilities of the interferometer, due to different effects: i) changes in the dielectric constant of the air, producing a wrong signal from the capacitance micrometers, ii) changes in the spacing between the pads of the micrometers, produced by thermal effects on the capacitor pillars, iii) electronic drifts produced by thermal effects on some components of the CS100.

Moreover, for what concerns the refractive index of the air, this obviously depends on the atmospheric changes of pressure, temperature and humidity.

The environmental effects on both the capacitance micrometers and the optical length of the cavity are easily eliminated by placing the interferometer in a sealed chamber. The residual thermal effects have then been eliminated by accurately thermostatizing both the interferometer and the electronics.

In particular, as the FPI has a thermal sensitivity of 3 mÅ C^-1, to obtain a wavelength stability of 1 ms^-1, the interferometer must be thermostatized within 5 10^-3 C. To this purpose the FPI chamber has been enclosed in a copper box, externally warmed by a sheet resistance, and covered by heat insulating panels; two fans mix the air to make the temperature uniform inside the box, and a thermostatic system allows one to obtain a thermal stability of 0.1 C at about 37 C. Then, a second sheet resistance, wrapped around the sealed chamber and controlled by a second independent thermostatic system, maintains the interferometer at about 38 C within 5 10^-3 C (Fig. 1 (click here)), for variations of 2 C of the ambient temperature.

  
Figure 1: Temperature inside the interferometer chamber vs. time. The temperature has been evaluated by measuring the resistance of a Pt100, with a resolution of 1 m ( 2.5 10^-3 C), and the fluctuations relative to the mean ( 38 C) have been plotted

As regards the CS100, its thermal sensitivity is 0.1 mÅ C^-1, and a thermostatization within 0.1 C, obtained by controlling the speed of two fans cooling the electronics, is therefore sufficient to secure the demanded wavelength stability.

Finally, to test the residual drift of the interferometer, the ¹¹⁴Cd red line at 6438 Å, emitted by an isotopic spectral lamp, has been used. The stability of this line (secondary wavelength standard) is 2 10^-8 , corresponding to 6 ms^-1 in velocity units (Engelhard & Bayer-Helms 1972).

The following assembly has then been used to perform the test. The interferometer, used in axial mode, was placed between two lenses: the first one collimates a pinhole, where a macrophoto lens forms an image of the lamp discharge tube, the second one forms an image of the pinhole on the cathode of a photomultiplier. A second photomultiplier, used as reference, directly sees, via a fiber optic, the light emitted by the lamp. The photomultipliers are both used in photon counting and are preceded by an interference filter, centered at 6438 Å, sufficiently narrow (FWHM = 50 Å) to isolate the Cd red line.

This assembly was first used to accurately measure the profile of the Cd line and to locate on it a linear range, which was found between 60 and 80% of the peak intensity. The two points, at the center of the linear ranges on the blue and on the red flank of the line, have been then located at 13 mÅ from the line peak.

Let us define now as velocity signal the quantity:

with

where , and respectively are the wavelengths of the line peak and of two points on the blue and on the red flank of the line; and are the intensities measured on and ; and are the corresponding intensities measured by the reference photomultiplier. Fixed = 26 mÅ, we have, within the linear range:

K has been then evaluated by a linear fitting of S, measured at five around ( = 1 mÅ). The so obtained value for K is:

It follows from Eqs. (13) and (14) that, if the wavelength stability of the interferometer must be measured within 1 ms^-1 ( 0.02 mÅ), we must be able to measure a variation . It is easy to show that, assuming , the rms errors on S and respectively are and . If we impose , we obtain therefore 10⁷ counts.

To measure this signal in a short time, a photon counting at frequencies of some MHz is obviously necessary. At this rate however the non linearity effects become relevant and the dead time of the chain formed by the photomultiplier, the amplifier-discriminator and the counter must be known. To this purpose, the following second assembly has been used. By means of a beamsplitter cube, the light emitted by a photodiode is seen simultaneously by the two photomultipliers. Between the diode and the cube a shutter allows one to measure the dark counting and a filter wheel, carrying a neutral density (D = 0.1), allows one to reduce the signal of a known amount. For each photomultiplier, the ratio R between the signals with and without density has then been measured at different light levels, up to 6.3 MHz. R has been then reported versus Log I, where I is the signal without density, and the dead time has been obtained by the best fit of the data. The same dead time has been found for the two photomultipliers (38 ns) and, accounting for it, the newly measured R are constant within 0.5%, up to 6.3 MHz.

The first described assembly, used to measure the profile of the Cd red line, has been then used to measure the wavelength stability of the interferometer. To this purpose, the position of the line peak has been located, and then the velocity signal S has been measured on two points at 13 mÅ from the line peak and on two other points at 14 mÅ. By using crossed polarizers, the signals on the two photomultipliers have been adjusted to 2 MHz and an integration time of 5 s has been used, to secure a sensitivity of 1 ms^-1. The measurement has been repeated each minute for two days and the results are shown in Fig. 2 (click here), where the wavelength drift, obtained by Eqs. (13) and (14), is plotted versus time. The curves a and b respectively refer to the measurements performed at 13 and 14 mÅ, and, for the sake of clarity, they have been arbitrarily shifted along the y axis. To evaluate the error on the measured drifts, the curve c has been then obtained as a difference between a and b. As it may be seen, c is a horizontal straight line with a superimposed noise, amounting to 0.85 ms^-1. If we suppose that the error on a and b is similar, we may conclude that the error on each measured drift is 0.60 ms^-1, significatively larger than the expected error = K^-1 = 4.9 10^-3 mÅ ( 0.23 ms^-1). This discrepancy can be explained as due to the electronic noise of the CS100, which causes the interferometer plates to make small amplitude random movements about their mean position. Queensgate claims an electronic noise equivalent displacement of the FPI plates amounting to 10 pm Hz^-1/2 (see Table 1 (click here)). For a 3 mm separation, this means a noise ms^-1 Hz^-1/2, where t is the integration time. If t = 5 s, the electronic noise will be therefore = 0.45 ms^-1, and finally the total expected noise, photometric plus electronic, will be 0.5 ms^-1, very similar to the measured value of 0.6 ms^-1.

 
Figure 2:   Wavelength drift of the Fabry-Perot interferometer vs. time. The curves a and b refer to independent measurements of the 6438 Å Cd line position, respectively at 13 and 14 mÅ from the line peak. For the sake of clarity, the two curves have been arbitrarily shifted along the y axis. The curve c, a horizontal straight line with a superimposed noise of 0.85 ms^-1, has been obtained as a difference between a and b

By carrying on the analysis of Fig. 2 (click here), it may be seen that the a and b curves show a very slow, nearly linear trend. From a linear fitting to the mean of the two curves, a drift of 0.014 mÅ h^-1 (0.65 ms^-1h^-1) is found. This drift, amounting to 0.67 mÅ (31 ms^-1) in 48 h, cannot be ascribed to the the spectral line, the stability of which is 6 ms^-1, neither to temperature effects on the interferometer, as shown by Fig. 1 (click here), but more probably to some electronic drift of the CS100. Other shorter measurements of the interferometer wavelength stability have been performed and different drifts have been found, but none larger than 5 ms^-1 has been observed over a period of ten hours.

Moreover, the residuals of the linear fitting, shown in Fig. 3 (click here), evidentiate wavelength instabilities amounting to 0.34 mÅ  (16 ms^-1) peak to peak. The cause of these fluctuations is not evident; their amplitude, however, very similar to the line instability, suggests that probably they must be ascribed to the spectral lamp, rather than to the interferometer itself. To test if these fluctuations could be ascribed to the lamp power supply, the recommended cathod heating current (0.8 A) and the discharge current (0.3 A) have been changed from 0.6 to 0.9 A and from 0.2 to 0.5 A respectively, but no variation on the velocity signal within 1 ms^-1 has been observed. It is evident, therefore, that to have a more accurate knowledge of the instrumental wavelength drift a more stable source, as, for example, a frequency stabilized laser, should be used.

  
Figure 3: Residuals of a linear fitting to the mean of the a and b curves of Fig. 2 (click here), showing wavelength instabilities amounting to 0.34 mÅ (16 ms^-1) peak to peak

In conclusion, after the inclusion of the interferometer in a sealed chamber and a careful thermostatization, the instrumental profile shows a very high wavelength stability: the maximum expected drift on 10 h, as in the case of a very long solar observation, is about 0.2 mÅ (10 ms^-1).

Anyhow, as a measurement of the instrumental wavelength drift demands a short time to be performed ( 2.5 s for an integration time of 1 s), such a measurement can be alternated to the observations and used to compensate the drift, by correcting the biasing voltage applied to the interferometer. However, in practice, because the smallest voltage step allowed by the CS100 corresponds to a wavelength shift of about 1 mÅ, too large with respect to the observed drift, this correction will seldomly be useful: when the instrument does not work correctly.

On the other hand, the measurement of the drift can be also useful a posteriori to verify the instrumental behaviour, and, in case, to correct the data for drifts exceeding the wavelength stability of the Cd lamp.