Molecular clouds at high galactic latitudes are the most promising hunting
grounds for neutron stars accreting from the interstellar
medium because:
(1) the density of the interstellar medium (ISM) is high
(
compared to typically 
or less
outside) and we therefore expect higher accretion rates and more
luminous sources;
(2) the increased column density through the cloud screens out
background sources;
(3) the location of the cloud at galactic latitudes above
cuts down the number of chance coincidences
with unrelated field stars.
An increased absorption due to the higher column density affects all sources and their spectra. For a single source population, distributed isotropically within the sampling volume, I therefore expect fewer and less luminous X-ray sources with on average harder spectra inside the projected boundaries of molecular clouds. Accreting compact objects show the opposite behavior because they are directly interacting with the material in the cloud. Prominent soft X-ray sources without bright optical counterparts are for this reason good candidates for accreting objects inside the clouds. However, high absorption due to material in the vicinity of the source can obscure accreting objects deep inside a cloud. These objects will be lost from the sample in the current search technique. For the time being, I assume that their number is small.
One sample of clouds is particularly well suited for this
search. Magnani, Blitz and Mundy, hereafter MBM, (1985)
published a comprehensive survey of the sky outside the galactic plane.
Areas of apparent optical
extinction at latitudes 
and declinations greater than
on the Palomar Observatory Sky Survey (POSS) and
the White Oak extension were identified by MBM through visual
inspection. These candidate areas were then observed at 115GHz with
the 5m telescope of the Millimeter Wave Observatory near Fort Davis,
Texas because emission at the CO (J = 1-0) transition frequency at
115.2712GHz is a tracer of molecular clouds.
Figure 1 (click here) shows the distribution in galactic coordinates of all
clouds detected in this survey. The apparent lack of clouds around
is due to the declination constraints of the survey.
Figure 1:
Distribution of MBM clouds in galactic coordinates. The mark C41
indicates the position of the cloud complex 41-44 that casts
a deep shadow on the diffuse soft X-ray background. An area
south of was not covered in this survey
because it is unaccessible to the Texas telescope.
Circles merely indicate the position of the cloud
Fiftyseven clouds in 35 complexes were detected at high galactic latitudes,
.
Additionally, 66 clouds were detected at intermediate latitudes
.
Twentythree of the complexes at high galactic latitudes were
later mapped to obtain their morphology. These 23 complexes cover an
area of 
. Including the clouds that have not been
mapped raises the area covered by clouds at high galactic latitudes
to 
.
The clouds at intermediate latitudes were not
mapped by MBM, therefore estimating the covered area in this region
is more difficult. An upper limit to the area is the area searched
in the ROSAT All-Sky Survey of 
per position.
The area searched at intermediate latitudes was 
.
The total area covered by clouds at high latitudes and at
intermediate latitudes is therefore 
.
MBM derive a range of densities for the mapped clouds
of 35 to 500
with a mean value of 140.
The velocity dispersion of the ensemble is 
and
the mean velocity with respect to the local standard of rest is
. The average distance to the clouds is
105pc and the mean radius of a cloud is 1.7pc.
I searched the ROSAT All-Sky Survey for sources that coincide with the
cloud sample of MBM. For clouds where no maps were given by the
authors, I used a search radius of 
around the position of
the cloud. For the mapped fields, I approximated the often complex
shape of the cloud with a mosaic of rectangles. The rectangles were
chosen with a generous overlap into empty areas, generally at least
. All X-ray events detected during the ROSAT All-Sky Survey
within the above areas were extracted from the archive. In a second
step I binned these event lists into images. On these images, I
performed a source detection, following the standard procedures for
ROSAT data with some adjustments for survey data. The procedure
consisted of an initial source detection, the creation of a background
model and a renewed source detection. All sources with smaller
separation than the point spread function of the telescope were merged
and a likelihood value for the existence of the source at that position
was calculated.
During the source detection I chose a reduced likelihood threshold of 8.0,
compared to the standard 10.0 value. Accepting a lower value for the
likelihood of existence of a source results in an increased number of
spurious sources.
These are mere fluctuations of the background and are not real objects on
the sky. However, the benefit of this is a higher sensitivity to faint
sources close to the detection limit of the survey.
In this manner, I find 353 sources within 
,
covering an area substantially larger than the area covered by the clouds.
I then compared the positions in this initial source list with the maps
published by MBM.
I considered any source found inside the lowest contour level of a cloud
as a candidate object and included it in the identification program. The
lowest contour in the CO maps of MBM corresponds to an antenna temperature
of 0.5K. For the unmapped clouds, a maximum
distance from the position of the cloud according to MBM of 20 arcminutes
was used as a cut-off. I intentionally set the cuts to err on
the side of inclusion rather than missing an interesting candidate.
Out of the initial 353 sources 90 sources are found
inside the projection of an MBM cloud. One source out of this
sample was later identified as a double detection leaving me with
89 sources.
The next step was a classification of all sources, based only on their X-ray characteristics. For faint sources the ROSAT Position Sensitive Proportional Counter (PSPC) yields only moderate energy resolution. However, the resolution is sufficient to parameterize the spectrum of a source by a hardness ratio. ROSAT hardness ratios are defined as the number of detected counts in the hard band minus the number of counts in the soft band divided by the total number of counts in the two bands. In this way, any source spectrum is related to a number between -1 for soft sources and +1 for hard sources.
The ROSAT band from 0.1 to 2.0 keV is split into four bands,
three of which are independent: A (0.1 - 0.4keV: 11-40),
B (0.5-2.0keV: 50-200),
C(0.5-0.9keV: 50-200) and D(0.9-2.0keV: 90-200).
The numbers after the colon indicate the selected ROSAT PSPC
pulse height channels.
The gap between 0.4 and 0.5keV is due to the carbon absorption edge
which renders the PSPC entrance window essentially opaque in this
energy range. The hardness ratios HR1 and HR2 are then defined
as the ratio of number of detected counts in the respective bands:
When a source is not detected in one of the bands a hardness ratio of -1 (for sources only detected in the soft band) or +1 (for sources detected only in the hard band) is assigned. For some faint sources it is only possible to determine HR1 and not HR2, because the source was detected neither in band C nor D. These sources shown an asterisk in the HR column in Table 2 (click here). Two sources are so close to the detection limit that no hardness ratios could be derived. The hardness ratios are generally uncertain in the last digit due to photon statistics.
Figure 2:
X-ray Color-Color diagram of the complete sample.
left: Single dots -- sources not coincident with clouds.
Dots surrounded by a circle -- sources inside of cloud boundaries.
Sources only detected in the soft or the hard band are
assigned -1 or +1 values.
right:
Histogram of source distribution in HR1 (bottom) and HR2 (top).
Unhatched histograms -- sources outside of clouds.
Hatched histograms -- source inside of cloud boundaries.
(Note: the histograms for HR1 are split
into two panels to account for the very high last bin)
Figure 2 (click here) shows the derived X-ray Color-color diagram, comparing all detected sources with the sources that coincide with MBM clouds. The distribution in the harder band, HR2, appears not to be affected by whether a source is found in front of a cloud or outside the projected boundaries of a cloud. This is not surprising as the column density through the clouds is not sufficient to significantly attenuate X-ray emission above 0.5keV.
In the softer band, HR1, a significant difference between the two
groups of sources is found. The ratio of the hardest sources
(
) to the total number of sources is the same for both groups.
However, the fraction of soft sources is much higher in the sample
coinciding with the clouds than in the sample outside of the clouds.
This finding does not match the expectation from the simple single-population source model. A possible interpretation is a two-population model: a soft, local population and a second hard, more distant population. The harder, preferentially fainter sources, fall below the detection limit of the survey due to the additional absorbing column through a molecular cloud. As a result the distribution is dominated by the soft, local component that does not suffer from absorption because of the proximity to Earth. The same effect is seen with much higher statistical significance in the sample of sources in galactic dark clouds, see Paper II.
For bright sources it is often possible to fit different source models to their X-ray spectra, to derive a goodness of fit parameter and then decide on the most appropriate model. However, my sources are in general too faint to derive well constrained parameters and I have to assume a source model.
My survey is driven by the idea that the dominant emission from slowly accreting sources will be well described by a black body spectrum. This surface emission has to penetrate intervening material in the immediate vicinity of the source and interstellar material between the source and Earth. These two components can be summarized in a single absorption column to the source. The initial source spectrum plus absorption form the source spectrum arriving at the telescope. This spectrum has to be folded with the energy-dependent vignetting of the imaging system and the detector response matrix.
The initial source spectrum, including absorption, can be written as:
where 
is the column density in 
, X(E) the
photo-electric absorption cross section, T the radiation temperature
and E the photon energy.
This source model was then folded with the detector response matrix
and integrated over the four energy bands. The result is a theoretical
X-ray Color-Color diagram for different source temperatures and
absorption columns (see Fig. 3 (click here)).
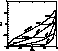
Figure 3:
Assuming a black body source spectrum, the expected hardness
ratios are plotted for four given source temperatures
(dashed lines) and a range of absorption columns.
Dotted lines indicate the ROSAT hardness ratios for a
given absorption column and a range of source temperatures
At the low end of the temperature range, up to 100eV, even small amounts of absorption will lead to a "hard'' value for HR1 because the band between 0.1 and 0.4keV suffers quickly from even modest absorption. This effect can easily hide intrinsically soft sources in the hard segment of the diagram. Conversely, HR2 responds much more slowly to absorption due to its higher energy. Therefore HR2 is a better parameter in searches for soft sources beyond the local void of the interstellar medium.
The most powerful classification parameter in the search for compact
objects is the ratio of X-ray to optical flux. Previous studies,
based on observation made with the EINSTEIN observatory, have pointed
out that there is a strong correlation between this ratio and a given
class of astronomical objects.
Maccararo et al. (1988) order the classes starting
with hot B and F stars with 
through
galaxies to AGNs and BL Lac objects with 
.
They used the following relation to calculate the ratio of X-ray
to optical flux (Maccacaro et al. 1988) where the units of the
X-ray flux are 
Obtaining CCD photometry on more than 350 sources as an initial screening procedure would require a prohibitively large amount of telescope time. Fortunately, digitized versions of the Palomar Observatory Sky Survey (POSS) and the UK-Schmidt plates are available. The CDROM set distributed by the Space Science Telescope Institute supplies data with a spatial resolution of 1.7''. Most of the northern hemisphere data is based on the red Palomar E-plates and the southern hemisphere data is based on the SERC Southern Sky Survey and the SERC J Equatorial extension.
The data from these CDROMs can be related to standard photometric systems.
However, the color systems of the ESO R and SERC J surveys
(magnitude mr, mj) are different from the BVR system
(mB, mV, mR).
I use the color transformation from Hörtnagel et al. (1992)
and invert their relations to get:
For the Palomar northern plates Humphreys et al. (1991) derive
the following color transfer function:
Ignoring all non-linear terms I simplify this to
I looked for a simple method to apply these relationships to the digitized sky survey data set. I used the standard photometry routine magnitude/circle in the MIDAS (Munich Image Data Analysis System) environment to determine "instrumental magnitudes'' from the DSS images and applied the above conversions. The result of this approximation for a set of Landolt standards is shown in Fig. 4 (click here).
Figure 4:
Magnitude calibration of the Digitized Sky-Survey data sets:
top: E-Plates:
triangles -- Landolt standard stars on same POSS I E-plate;
dots -- stars from Humphreys et al. from three other POSS I
E-plates. A single line is fit to the data for simplicity.
bottom: IIIa-J-Plates:
Different symbols mark Landolt standard stars from three
plates
Standard stars on the same survey plate follow closely
a linear relation between my derived instrumental magnitudes
(
) and the magnitudes calculated from the Johnson BVR
system (
, 
). Because I did not include a correction for
different exposure times for each plate, a larger scatter was introduced.
This is in particular visible in the plot for the J-Plates. For simplicity I
ignore these various offsets, which appear to be of lesser importance for
the E-Plates, and fit one regression line for each plate set:
This rule of thumb serves my purpose of making an initial estimate of
the X-ray to optical flux ratio well, but has to be treated very
carefully in individual cases. Large color terms can
render the estimate meaningless due to the involved systematics.
Notwithstanding the above argument, the derived values are an important
tool to classify quickly large numbers of sources without any telescope
time. For the future, STScI has announced the completion of a
calibration set for each individual survey plate that will take
individual offsets into account and will yield much more reliable
numbers. Currently only one plate of the POSS survey is included
in the DSS for each position on the sky and it is therefore not
possible to derive color-information from the DSS.
Further assumptions have to be made to estimate the X-ray flux
of each source.
Most survey sources (with integration times of only 
) did
not collect enough photons to extract a meaningful spectrum.
In the absence
of more information on the source spectrum I apply the rough rule
for ROSAT: 1 cnt/sec = 
(ROSAT User Handbook, MPE 1997).
As I lack all color information on the optical counterparts, I replace mV
with the magnitudes in the photographic pass bands , 
of
the survey plates and obtain:
where 
is replaced with either 
or 
,
whichever is available.
Figure 5:
Distribution of the logarithm of the optical to X-ray flux ratio
for different subsamples. Number of sources
per logarithm bin:
A) all 353 sources;
B) only sources inside the projection of an MBM cloud;
C) soft sources with a HR1<0;
D) distribution of soft sources (HR1<0.0) that coincide
with clouds
The distribution of this ratio is plotted for all 353 detected
sources in Fig. 5 (click here). The four panels in this figure show
the distribution of the X-ray to optical flux ratio for all
sources (panel A) and three other sub groups. The distribution
of this value does not vary significantly for sources found
coincident with clouds (panel B), although there
might be a hint of fewer sources with high values of
.
The soft source population, where HR1<0.0, has a strong signature
of sources with bright optical counterparts and
between
-4.5 and -3.5. Finally, the soft sources, HR1< 0.0 that
coincide with clouds appear to be completely devoid of sources with
high values for this ratio.
In the search for point sources I also discovered a previously
undescribed extended feature. The MBM clouds 41 through 44 cast a
distinct shadow on the soft X-ray background. The left panel in Fig.
6 (click here) shows the ROSAT image in the 0.1 to 0.4keV range. The right
panel shows an image from the IRAS 
m survey of the same
area. Numbered crosses mark corresponding coordinates in the X-ray and
the IRAS image. A lighter shade corresponds in both images to a higher
intensity. The intensity of areas with reduced diffuse X-ray emission and
outside differs by up to a factor of 2.5. The structure of the
diffuse background as seen with ROSAT has been most recently described
by Snowden et al. (1995). Shadowing structures have been
described on several occasions in the past (e.g. Snowden et al.
1993). However, the complex of clouds 41 to 44 casts one of the
cleanest and deepest shadows so far identified. The absorption contours in
the X-ray image accurately trace the areas of emission on the IRAS image.
The IRAS image shows that the apparently isolated peaks of CO emission
(Magnani et al. 1985) belong in fact to the same structure.
Figure 6:
ROSAT All-Sky Survey image of MBM clouds 41 to 44
(left) and IRAS 100
image of the same region (right).
Numbered crosses mark corresponding locations on the sky.
In both images lighter shades indicate increased emission.
The shadow on the diffuse X-ray background (left) closely matches
the bright emission band in the infrared image (right).
The images extend over approximately 3 by 3 degrees, north
is up and East to the left