An azimuthal asymmetry of the geometry of the light scattering by non-spherical particles (see Fig. 1 (click here)) provokes the non-coincidence of the directions of the radiation pressure force and of the wave-vector of incident radiation. This fact was mentioned in the literature (e.g., Kerker 1981) but the detailed consideration has been made only for infinite cylinders (Voshchinnikov & Il'in 1983a) and spheroids (Voshchinnikov 1990).
Figure 1: Geometry of light scattering by a prolate spheroid
with a/b=4. The wave-vector of incident non-polarized radiation
forms
the angle 
with the rotation axis of spheroid.
Short-dashed curve shows the angular distribution of
the scattered radiation (phase function).
The part of scattered radiation which is symmetric relative to the direction
of incident radiation is plotted by long-dashed curve.
The directions of the resulting radiation
force as well as its components in the radial and transversal directions
are indicated
The radiation pressure force on a non-spherical particle
may be written as follows:
where 
is the flux of non-polarized radiation of
a point source at frequency 
,
c the velocity of light,
and 
are the unit vectors
in the radial and transversal directions (
,
, 
is the wave-vector of incident
radiation), and
the radiation pressure cross-sections
for the corresponding directions.
We approximate the flux in Eq. (4 (click here)) by the Planck function
with the effective temperature of the star 
and
consider the Planck mean cross-sections and efficiency factors
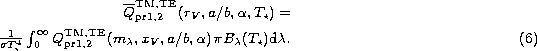
Here, 
is the Stephan-Boltzmann constant,
the refractive index of the grain material,
the size parameter,
the angle between the rotation axis of
the spheroid and the wave-vector (
),
G the geometrical cross-section of a spheroid (the area
of the particle shadow) that is
for an prolate spheroid and
for an oblate spheroid.
The superscripts TM and TE are related to two cases of
the polarization of incident radiation (TM and TE modes).
The efficiency factors 
are calculated from
the solution to the light scattering problem for spheroids
(see Voshchinnikov & Farafonov 1993 for details).
For both modes, they can be expressed as follows:
where 
is the
extinction efficiency factor,
and the coefficients 
and 
are
In Eqs. (11 (click here)) - (12 (click here)), 
is a parameter,
the dimensionless intensity of scattered
radiation (phase function; Fig. 1 (click here)).
From a symmetry consideration, it is clear that for spheroids
if 
or 
. The detailed expressions
for calculations of the factors 
are given in the paper of
Voshchinnikov (1990).
For randomly aligned particles, the Planck mean cross-sections
have to be averaged over all orientations
For perfect dynamical alignment, the Planck mean cross-sections
are averaged over all rotational angles 
.
This gives for prolate spheroids
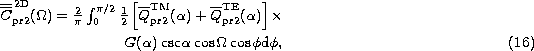
where the angle is connected with 
and
(
). For oblate spheroids randomly aligned
in a plane, we have 
and
The radiation pressure force 
is
the main force acting on dust grains in the envelopes of late-type giants.
Its ratio to the gravitational force 
is much larger than 1 in almost all cases
(Voshchinnikov & Il'in 1983b).
As weak magnetic fields and small electric charge on grains
are expected in the envelopes,
we can neglect the Coulomb drag and Lorentz forces
(see Il'in 1994 for details).
Thus, the equation of the stationary grain motion should be
where 
is the drag force due to collisions of a grain
with surrounding gas particles.
It is proportional to the gas density, the grain velocity relative to the
gas 
, and
the geometrical cross-section of the grain.
For rotating grains, the averaged geometrical cross-section
or 
should be used.
The corresponding expressions are given in Appendix A.
The force is antiparallel to 
for spherical particles.
For non-spherical grains and subsonic drift velocity,
the angle between these two vectors depends on the type of reflection
of the gas particles from the grain surface.
If the mirror reflection occurs, then is perpendicular
to the major semiaxis of a spheroidal grain; for diffuse reflection,
forms a small angle with 
,
and the value of this angle depends on the difference between the gas and
dust temperatures. The angle should be close to zero
for any type of reflection in the case of supersonic drift velocity.
From the equation 
,
the mean drift velocity of a rotating grain is
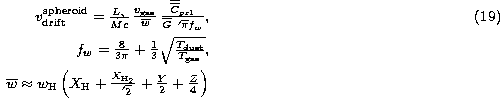
for subsonic motion
and
for supersonic motion.
Here, 
is the stellar luminosity, 
the mass loss rate,
the sound velocity, 
are
the relative abundances (by mass) of hydrogen (atoms and molecules),
helium and heavy elements, respectively.
Thus, the ratio of the drift velocities
for spheroidal and spherical particles of the same volume
is determined only by the cross-sections of the particles
where n = 1 for subsonic motion and n = 2 for supersonic motion.