The light curve,
The light curve mapping program presented here allows one to model
a light curve of a cataclysmic variable star, or any related
object. The model comprises an accretion disk and a Roche-lobe
filling secondary star.
The disk can assume nearly any three-dimensional shape.
The surface of the disk and the star are approximated
by a grid of tiles.
Given some combination of orbital inclination and stellar
masses, ray-tracing determines what fraction of each grid
element is visible at any orbital phase.
Each element is assigned an intensity value.
The total brightness observed from the system is the weighted
sum of intensities, Fi, of all individual elements, i.
The weight includes (a) the fractional
visibility of the element, (b) its surface area,
(c) the fore-shortening projection factor onto the plane of view,
and
(d) a limb darkening factor (optional; limb darkening may assume
its quadratic or linear approximation, or any other functional
dependence; see Wade & Rucinsky (1985) for limb darkening
coefficients for stars, and Diaz et al. (1996) for accretion
disks).
The light curve, ![]() , is derived by conducting this summation as
a function of orbital phase
, is derived by conducting this summation as
a function of orbital phase ![]() .
The visibility matrix
.
The visibility matrix ![]() accounts for the weight
factors for all grid elements, and as a function of orbital phase.
Thus,
accounts for the weight
factors for all grid elements, and as a function of orbital phase.
Thus,
![]()
By comparing the calculated light curve for some grid
brightness distribution with the measured light curve, the
intensities Fi of the grid elements can be adjusted
iteratively until the measured light curve is optimally fitted.
Within the uncertainty on the light curve, however, many different
solution are possible that fit the light curve equally well.
In order to obtain the smoothest possible, unique solution which
fits the data to a reduced ![]() of unity an additional constraint
is needed. This is found in the so-called entropy function
which is maximized.
The maximum-entropy solution to some problem may be looked upon
as the most likely
solution out of the ensemble of all possible solutions.
of unity an additional constraint
is needed. This is found in the so-called entropy function
which is maximized.
The maximum-entropy solution to some problem may be looked upon
as the most likely
solution out of the ensemble of all possible solutions.
The entropy value of an image is measured relative to some default image. The final maximum-entropy solution will tend towards the default image as much as the constraint imposed by the light curve and the associated uncertainties will allow. Following Horne (1985, who pioneered the application of the maximum-entropy criterion in the analysis of eclipse light curves in CVs), the default image for the accretion disk is taken to be the azimuthally averaged map of the solution itself. For the surface of the secondary star the default image is taken to be a straight average of all grid intensities. This choice of the default image optimises the solution for studying radial brightness structures on the disk, and it tends to supress structure on the stellar surface. More details on maximum-entropy optimization may be found in, for instance, Burch et al. (1983), Skilling & Brian (1984), and Skilling & Gull (1985).
In this light curve fitting technique the basic assumptions are that the secondary star fills its Roche lobe, the geometry of the binary system and the three-dimensional shape of the accretion disk is defined, and the orbital inclination is known. Furthermore, the intensity distribution with respect to the co-rotating frame must not change with time.
The grid consists of a large number of triangular tiles which together shape the surface of the accretion disk and the Roche-lobe filling star. The disk surface is build up around a Cartesian grid in the orbital plane. A third orthogonal coordinate is added to each point in the plane to define the disk's three-dimensional shape. The disk grid possesses a top and bottom surface, which allows for a realistic representation of the disk rim, and also allows accurate modelling of tilted disks. Within the three-dimensional shape of the disk, transparent - ``optically thin" - surface elements may be defined. An example of a grid structure is shown in Fig. 1 (click here).
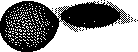
Figure 1: An example showing the geometry of a grid of surface elements,
comprising the secondary star and
the accretion disk. The accretion disk is flaring out towards the edge.
The mass ratio is unity and the inclination angle is 70 degrees
The fact that the disk may assume some three dimensional geometry aggravates the problem of obtaining a unique solution, in particular in conjunction with the secondary star. A high level of ambiguity in the solution may be present, depending on the exact geometry. Such ambiguity arises when light coming from different parts of the binary system have similar impact on the light curve. Bright (or dark) structures on for instance the rim of a thick disk can in some cases be incorrectly interpreted as a brightness structure on the star, since both result in a similar phase-dependent contribution to the light curve. In such situations the light curve can not be used to distinguish between the different brightness structures, and the final solution is defined by the entropy constraint, not by the data. Light curves from eclipsing systems provide the best information on the brightness distribution and allow most accurate distinction between bright structures on the star and the disk. Even more so than in the case of standard eclipse mapping, with 3D light curve fitting results must always be treated with caution, and simulations must be carried out for each choice of geometry in order to understand and eliminate spurious results.
The vast range of possibilites in choice of geometries makes it virtually impossible to characterize the 3D light curve program in a general sense. The parameter space is too large to describe for all possible geometries how uncertainties on the light curve, or errors on the assumed geometry or on the binary system parameters affect the resulting maps. One qualitative example is presented in the next section. Apart from the flexibility in geometry, this technique is comparable to the standard eclipse mapping technique, and similar limitations and considerations on its use apply (see Horne 1985, 1993).