2. Method

2.1. The logarithmic transformation

Practical experiments with the surface curvature of astronomical images have soon revealed to us the superiority of dealing with the logarithm of the intensity, , rather than with the intensity itself. The justifications of this transformation are easily understood:

i)

The range of curvatures will be narrower on the images than on the intensity images insuring a better detection of faint objects;

ii)

Point-like objects such as stars may be viewed, at least in a first approximation, as having a Gaussian shape. The logarithmic transformation will generate similar paraboloids (i.e. having the same parameters) for which the maximum of curvature takes place at their tops. Practically, the logarithmic transformation of the star images will exhibit a coarse paraboloidal shape which will be easily localized from the maximum of curvature.

2.2. Surface curvature

Let x and y be the two spatial coordinates and , the log transform of the intensity value. We now closely follow the formalism introduced by Peet & Sahota (1985) and specify any point on the surface by its position vector:

The first fundamental form of the surface is the expression for the element of arc length of curves on the surface which pass through the point under consideration.
It is given by:

where

The second fundamental form arises from the curvature of these curves at the point of interest and in the given direction:

where

and

Casting the above expression into matrix form with:

the two fundamental forms become:

Then the curvature of the surface in the direction defined by V is given by:

Extreme values of k are given by the solution to the eigenvalue problem:

which gives k₁ and k₂, the minimum and maximum curvatures, respectively. k₁ and k₂ are invariant under rigid motions of the surface. Two other curvatures are often defined, the Gaussian or total curvature K = k₁ k₂ and the mean curvature M = (k₁ + k₂)/2 but it turns out that the principal curvatures k₁ and k₂ are best suited to the detailed characterization required by our problem.
As curvature is a geometric property of surfaces, we must introduce a continuous representation of the discrete 2-dimensional array of data in order to calculate local derivatives and then, local curvatures. We retain the so-called facet model (Halarick 1984) which considers a square window of data points (L is an odd integer) centered on the pixel of interest and calculates the 2-dimensional polynomial fit of degree N (), satisfying the criterion of least square errors (other functional representations may be chosen, see Laffey et al. 1985). This polynomial represents the local continuous surface with continuous derivatives up to order N. The window size L can, for instance, be adapted to the spatial extent of the Point Spread Function (PSF). It is very often the case in astronomical images that the PSFs are undersampled; then the lowest size corresponding to L = 3 is retained so as to minimize the error introduced by the facet model. This, in turn, maximizes the chance of detecting point-like objects but may result in a large number of false alarms due to local noise (e.g. noise spikes). When the ultimate goal is to restore the background, a trade-off should be reached which insures a minimal percentage of valid pixels as discussed in Sect. 4 (click here). When the PSFs are oversampled, then a larger size is recommended to limit the false alarms. For the simple facet model of second order, i.e. a window implemented in our examples, the surface is approximated by a quadric

and the practical calculation of k₁ and k₂ is extremely simple.

It is quite convenient to discuss the surface curvature in the (k₁, k₂) space as illustrated in Fig. 1 (click here). With the above convention and only the corresponding half plane is therefore allowed. Also, according to the above definitions, if a curve on the surface is concave up, the surface curvature in that direction is positive and vice-versa. The allowed half-plane of Fig. 1 (click here) is divided in three regions by the k₁ and k₂ axis. The two axis themselves correspond to parabolic points, ridges on the k₁ axis (k₁ < k₂ = 0) and valleys on the k₂ axis (k₂ > 0 = k₁). The second quadrant k₂ > 0 > k₁ is the region of the saddle points. The elliptic points are located in the remaining two half-quadrants, distinguished by their concavity : pits for k₂ > k₁ > 0 and peaks for k₁ < k₂ < 0. Obviously, a flat is at the origin k₁ = k₂ = 0.

  
Figure 1: Surface curvature visualized in the plan of the two principal curvatures k₁ and k₂

  
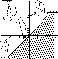
Figure 2: A practical k₁, k₂ diagram for an astronomical image. The regions of interest are related to specific parts or curvatures of real objects