for minima
During the observations of XY UMa in this work,
times of four primary and two secondary minima were
obtained and are given in Table 2 (click here). The 
values were computed using the following light elements
given by Geyer et al. (1955):
| H JD | Min | Filter |
|  |
| 2400000.+ | ||||
| 49433.5427 | I | B | 0.0088 | -0.0001 |
| 49433.5436 | I | V | 0.0097 | 0.0008 |
| 49436.4161 | I | B | 0.0082 | -0.0007 |
| 49436.4175 | I | V | 0.0096 | 0.0007 |
| 49443.393 | II | V | 0.0397 | ...... |
| 49443.395 | II | B | 0.0417 | ...... |
|
|
Figure 3: The versus epoch numbers diagram for XY UMa
The diagram of XY UMa is shown in Fig. 3 (click here).
This diagram contains other times of minima which
can be found from the literature: Apart from our minima we used
all visiual, photographic, and photoelectric minima
from the list compiled by Pojmanski &
Geyer (1990), and BBSAG observers, and Hanzl (1991),
and two photoelectric minima observed
recently by Jeffries et al. (1995).
deviations in Fig. 3 (click here) were calculated
with the ephemeris given in formula (1).
The arbitrary weights of the points were chosen from
Pojmanski & Geyer (1990). So, small points on
this diagram represent uncertain data of weight 0.
Photographic and photoelectric data are
represented by filled dots of sizes proportional to
their weights. Also, asterisks on this diagram represented
the residuals of secondary minima.
As it is clearly seen from the figure, the orbital period of XY UMa
changes with time. However, as it was stated by Pojmanski &
Geyer (1990), the asymmetry seen in the vicinity
of the secondary minimum affects the precise determination of the times
of secondary minima, and accordingly, in the period analysis of
XY UMa only the residuals pertaining to the times
of primary minima were used as it was the case with earlier works.
In order to calculate the phases of the observations of XY UMa,
the light elements of the system have been derived by using
the photoelectric primary minima times with E > 17000
cycles (see Fig. 3 (click here)) as;
with the weighted least squares method. In the light curves
which were formed using these phases, primary minimum
coincides with the phase 0.0 (see Fig. 1 (click here)).
The diagram of XY UMa in Fig. 3 (click here) indicates that the orbital
period of the system is changing in a sinusoidal character.
There are two mechanisms which explain such periodic orbital
period variations of eclipsing binary systems:
(i) a third body, and (ii) apsidal motion. Apsidal
motion is unlikely in the case of XY UMa, since
the orbital eccentricity of XY UMa is too small, and
the residuals of primary and secondary minima
times do not give a sinusoidal curve caused by apsidal motion
(i.e, times of secondary minimum of XY UMa in
Fig. 3 (click here) do not trace out a sinusoidal curve of equal amplitude
but exactly 
out of phase to a sinusoidal curve
traced out by times of primary minimum).
Therefore, the third body hypothesis can explain
the sinusoidal variation of the orbital period of XY UMa.
However, if this sinusoidal variation
character is, in fact, shape of the orbital period modulation,
the Applegate mechanism can explain orbital period modulation
of XY UMa. We shall investigate these suggested two models in turn.
Such an curve in Fig. 3 (click here) could easily be represented
with a light-time effect which results from orbiting around
a third body. According to third body hypothesis,
time delay which are resulting from the movement on the
eccentric three body orbit may be calculated as follows (Irwin 1959):
where a sini is the projected distance of the third-body
to the eclipsing pair (in km), c is the speed of light (in km/day).
e is the eccentricity; v is true anomaly;
is the longitude of periastron passage of
the orbit of three-body system, while 
is the epoch of periastron
passage and 
is the period of the orbit of three-body system.
The ephemeris for the minimum is now given by:
Unfortunately, the theoretical curve given this formula
do not fit to the old photographic data of Geyer (1977).
Therefore, a quadratic term (= 
) was added to
the Eq. (4):
where Q is the coefficient of the quadratic term and
gives change (increase or decrease) of the orbital period
of the eclipsing binary (in day). Finally, using Eq. (5)
to observed minima times of XY UMa, we have
performed the weighted regression method with
differential correction for T0, P, Q, 
i, e,
, ,
and parameters which are given in Table 3 (click here).
| Parameter | Value | Standart deviation |
| T0 HJD | 35216.5039 | 0.0013 |
| P (day) | 0.47899433 | 1.30 10-7 |
| Q (day) | 1.85 10-11 | 3.38 10-14 |
 i (km) |  |  |
| e | 0.41 | 0.09 |
|
|  | 12 |
|
(cycles) | 16205 | 3739 |
|
(cycles) | 24804 | 1168 |
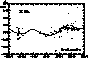
Figure 4: The versus epoch numbers diagram for XY UMa.
The residuals were calculated according to
linear part of the ephemeris given in Table 3 (click here).
The continuous line represents
an appropriate fit to the data
The Q parameter in Table 3 (click here) shows that the orbital period of XY
UMa is secularly increasing. The period increase is found
to be about 
s per century.
The mass transfer and mass loss phenomena can
be held responsible for the secular increase seen in
the orbital period of the system. Furthermore, existence of
MgII emission lines which is believed to be originated from
the circumbinary environment (Gurzadyan & Cholakyan 1995)
supports this proposal. The primary component of XY UMa is close to
fill out its Roche lobe (see Sect. 4). So, this primary component may be
responsible for the mass loss.
The orbital period increase of XY UMa and the
mass of the mass losing primary component greater than
the mass of other component indicates that the only case IV
from mass-loss cases discussed by Singh & Chaubey (1986)
is possible to XY UMa. The mass loss in the case IV
in which the ejected material escapes out from
the binary system may be calculated as follows:
Using Eq. (6) to m1=0.90 
and
m2=0.75 which are given in Sect. 5,
we have calculated 
for the mass loss rate for primary component to
observed value 
.
The 
residuals of all observed minima times of
XY UMa which were calculated according to the linear part
of the ephemeris given in Table 3 (click here)
are plotted versus epoch numbers in Fig. 4 (click here). In this diagram the
theoretical curve of the light-time effect is also plotted.
The parameters given in Table 3 (click here) show that the eclipsing pair
revolve around a center of mass of the three body system
with a period of 32.5 yr. The projected distance of the
third-body to the XY UMa is 1.487 AU. These values
lead to a small mass function of f(m3) = 0.0031
for the hypothetical third-body.
So, the masses of the third-body were computed for
different values of the inclination of three-body system and
are given in Table 4 (click here). In this computation m1=0.90
and m2=0.75 which are given in Sect. 5 were applied.
| Inclination | m3 () |
 | 0.483 |
 | 0.361 |
 | 0.297 |
 | 0.259 |
 | 0.237 |
 | 0.225 |
 | 0.221 |
According to Table 4 (click here) the minimum mass of the third-body was
found to be 0.22 . This value is different from
that found by Pojmanski & Geyer (1990) for third-body hypothesis
on XY UMa. The cause of this difference is that Pojmanski and Geyer
have been fixed the orbital period on the least square fitting process
for the light-time effect since the earlier photographic data
could not be fit. Instead of this artificial method
applied by Pojmanski and Geyer on analysis of XY UMa,
in this work, a quadratic term was added to Eq. (4)
given for light-time effect and all the parameters
were left free on fitting process. Such a method could be
considered more reliable since it does not include
an artificial effect in the process of fitting
a theoretical curve to data.
If the relative orbital inclination of three body system is equal to orbital inclination of XY UMa, the semi-major axis a3 of the third-body orbit around the center of mass of the triple system is about 11.2 AU. This value shows that the third-body, if it exists, revolves around much beyond the outer Lagrangian points of XY UMa and its orbit should be stable.
If the third-body is a main-sequence star,
the mass-luminosity function (
)
for the main-sequence stars with 
given by Demircan and Kahraman (1991) gives the bolometric absolute
magnitude of the third-body 
.
Whereas, the bolometric absolute magnitude of XY UMa
is obtained to be about 
in the
photometric analysis in this work. So, the third-body is
more than about 
fainter than XY UMa,
and then the lines of the third body on the
spectrum of XY UMa are unobserved. If one considers the distance
to XY UMa as 100 pc given by Dempsey et al. (1993),
the separation between the tertiary
body and the eclipsing pair may be found as 
.
As a result, either the faintness of the third-body in
the system or its small separation with the
eclipsing pair makes its direct observation with
the current equipment
almost impossible, leaving the third-body hypothesis in dark.
Zeilik (1997) has found the evidence for a third light from another star in his recent photometric analysis. He stated that if the maculation effect is large, and centered around zero degrees, the timing may be in error. So, he found that one have to use clean light curves to get the correct times for the primary minima in such cases. But, the main problem is, in his work, to correctly determine the effects distorted the light curves, and then to correctly clean the distributive effects from the light curves. It can be clearly seen that the probable errors in the cleaning processes will damage both the naturalness of the light curves and the normal light curves.
At this stage of the orbital period analysis, the cause of the orbital
period change in XY UMa is thought to be caused by
the period modulation of the sine variation.
Therefore, the sinusoid with amplitude 
, period and
a moment of minimum was added to the ephemeris (T0 and P)
to get the best fit to the data:
However, a quadratic term (= ) was added to
this equation since the earlier photographic data
could not be fit. So, using the sine equation
with a quadratic term to all observed times of minima of XY UMa,
we have performed the weighted regression method
with differential correction for
T0, P, Q, , and parameters.
The parameters found are given in Table 5 (click here).
| Parameter | Value | Standart deviation |
| T0 HJD | 35216.5021 | 0.0011 |
| P (days) | 0.47899433 |  |
| Q (days) |  |  |
|
(days) | 0.0079 |  |
|
(cycles) | 12953 | 190 |
|
(cycles) | 23713 | 615 |
|
|
Figure 5: The versus epoch numbers diagram for XY UMa.
The residuals were calculated according to linear
part of the ephemeris given in Table 5 (click here).
The continuous line represents
an appropriate fit to the data
According to this Q parameter, the increase in the orbital period was
found to be 
s per century.
This increase in the orbital period is related to the case IV
from mass loss cases discussed by Singh & Chaubey (1986).
Accordingly, the mass loss rate for the primary component is
estimated to be 
.
The 
residuals of all observed minima
times of XY UMa which were calculated according to the
linear part of the ephemeris given in Table 5 (click here)
are plotted versus epoch numbers in Fig. 5 (click here)
together with the theoretical curve of the sine equation with a
quadratic term.
The primary component of XY UMa is a RS CVn type star with a surface magnetic activity. The star-spot activity is evident from the light curve analysis in this work (see Sect. 4). So, for the cause of the orbital period changes seen in the system, the activity in the primary component might be taken responsible and the Applegate gravitational coupling mechanism (Applegate 1992) can explain the sinusoidal variation seen in Fig. 5 (click here).
The Applegate mechanism requires that the active star be variable,
and that the period of the luminosity variation
be the same as the period of the orbital period modulation.
Applegate (1992) explains that maximum luminosity should
coincide with an curve minimum if the star's outside
spins faster than its inside but should coincide with an
curve maximum if the outside spins slower than the inside.
In the case of XY UMa, Geyer (1976) has presented that
the average brightness of the binary system changed between
1955 and 1975 in a sinusoidal manner by 0.18 mag in V
and 0.20 mag in B, indicating a periodic variation
of about 28 to 30 years, and that the lowest
system brightness was observed in 1961, and the highest in 1975.
According to Geyer's paper, the mean brightness
and the orbital period of XY UMa vary
with the same cycle length, 
years.
But, the maximum system brightness in 1975 or minimum
system brightness in 1961 does not coincide with the
minimum or maximum of curve in Fig. 5 (click here). However, due to the big
asymmetries in the light curves of the system and insufficient data,
this conclusion could not be taken as final.
Only systematic and continuous observations may help to
decide on the existence of any connection between
the mean brightness and period variations.
Here, we use Applegate's
formalization in an effort to examine the orbital period changes
of XY UMa. We assume that the characteristics
of the active 
component of the system are:
, 
, and 
given in Sect. 5.
(i) The diagram of XY UMa in Fig. 5 (click here)
shows a modulation with a semi-amplitude of 
day and a modulation period of 
yrs.
This gives the observed orbital period change of
0.181 s. (ii) The angular momentum transfer,
which produces the 0.181 second period change, has been computed to be
.
(iii) The moment of inertia of the shell has been
computed to be 
by assuming
the mass of the shell is one-tenth of the active component's mass.
(iv) The variable part of the differential rotation is
. (v) The energy required to transfer the
angular momentum is 
ergs.
(vi) If the energy requirement is
supplied by the nuclear luminosity of the star with
no energy storage in the convection zone,
the star will be variable with the RMS luminosity variation
of 
which give rise to
only about 
mag light variation of the system.
(vii) The mean subsurface magnetic field which is
provide the RMS torque required to periodically exchange
between the outer shell and
inner part of the star is obtained to be about 10 k Gauss.
If the hypothesized magnetic cycle can be estimated from
an diagram as the time between one period decrease
and the next (Hall 1990), the diagram
for XY UMa in Fig. 5 (click here) gives the magnetic cycle of
the primary component as 31.1 yrs.
This value agrees with the magnetic cycle for solar-type dwarfs
computed by Hall (1990). Finally, the Applegate model gives
reasonable solution to the orbital perid modulation of
XY UMa which is caused by the
magnetic activity of the primary component.