2. RASS data and detection of late-type stars

2.1. The ROSAT all-sky survey (RASS)

During the first half year, the ROSAT observatory carried out the first all-sky survey with an imaging X-ray telescope. The whole sky was scanned along great circles perpendicular to the direction to the Sun. Because of the Earth's motion around the Sun, the plane of these circles slowly rotated around an axis through the ecliptic poles, thus covering the whole sphere within 6 months. Each point of the sky was observed several times as the scan paths of 2 degrees width (i.e., the field of view of the PSPC detector) progressed along the ecliptic. Therefore, the data of any particular source consist of a number of "snapshots'' of up to 30 s duration, separated by the orbital period of the satellite () and distributed over an interval of at least 2 days. Towards the ecliptic poles, the cumulative exposure time increases due to the larger number of scans covering a particular position. Depending on the ecliptic latitude (and down-time due to radiation belts of the Earth), the effective exposure time varies between and (at the poles), with typical values of on the ecliptic. Given a typical energy-conversion factor for soft sources of (cf. Sect. 2.4) the typical detection limit of RASS observations (i.e., ) amounts to . For a more detailed description of the RASS we refer to Voges (1992) and Belloni et al. (1994). Details of the ROSAT observatory in general can be found in Trümper (1983) and Trümper et al. (1991), the PSPC detector used during the RASS is described by Pfeffermann et al. (1986).

The source detection was performed by means of a maximum likelihood algorithm (Cruddace et al. 1988) in the course of the standard analysis software system (SASS; Voges et al. 1992). The significance of an X-ray source is expressed by the likelihood ), where P is the probability of existence; e.g., a likelihood of Li = 7 corresponds to a source existence likelihood of 99.9%. The result of the SASS is a comprehensive list of several 10⁴ sources, each source described by the sky position in RA and Dec., its source detection likelihood, count rate, hardness ratio, extent, and corresponding errors. The data for the brighter X-ray sources have recently been released as the ROSAT All-sky Survey Bright Source Catalogue (Voges et al. 1996b), which contains sources with Likelihood and count rate larger than , that have at least 15 photons.

2.2. Selection of stars

We used the Bright Star Catalogue (BSC; Hoffleit & Warren 1991) as input sample for our search of X-ray bright late-type giants. Specifically, we selected the stars according to their spectral classification, i.e., all stars of spectral types A, F, G, K, M, and C and luminosity classes I, II, III or intermediate classes (including III-IV). We further included those stars without MK spectral classification but with the old Harvard prefix "g'', and we also included all composite-spectrum stars with at least one component being of the abovementioned kind. Since the BSC is complete down to apparent visual magnitude and has a rather sharp cut-off at , the input sample forms a well defined (optically) flux-limited sample of stars. Given that stars of luminosity class III (or brighter) are normally absolutely brighter than , nearly all giants within a space volume of about 100 pc radius around the Sun are included in the BSC. In total, our input sample contains 3839 stars.

Since about 1 percent of the sky was not included by the RASS, a few BSC stars are not covered by X-ray observations. Those stars with less than 50 s exposure time are listed in Table 1 (click here).

 

HR Name Sp. type V

276 G8III 6.32

437 G7IIIa 3.62

527 G9III 5.91

731 27 Ari G5III-IV 6.23

904 7 Eri M1III 6.11

935 M3III 5.27

959 K1III 6.15

1195 G9II-III 4.17

1285 K0III 6.59

1316 K3-4III 6.71

2851 F0III 5.25

2864 6 CMi K1+IIIBa0.4 4.54

2917 K2III 6.76

2955 G8III 6.19

2965 M2IIIab 5.77

2967 M3II-III 5.56

2974 G20-Ia 6.56

2995 G6/8III 6.89

3095 1 Cnc K3+III 5.78

3376 K0III 6.28

3390 K3III 6.24

3426 A6II 4.14

3444 M0III 5.71

3445 F3Ia 3.84

3452 A5II 4.77

3461 K0III-IIIb 3.94

3477 G5III 4.07

3487 A1III 3.91

3496 F2Iab 5.75

3520 A2III 4.93

3534 G8III+A3-5V 6.42

3978 K1III 6.52

4007 M3III 6.40

4128 M2IIIe 6.43

4538 G6Ib 4.97

4704 K0III 5.74

4972 A8II-III 6.33

5122 K1III 6.42

5124 G5Ib 6.01

5251 G8-K0III 5.91

5362 G8III 5.56

5419 K1III 5.97

6076 K5III 6.29

6078 K4III 5.94

7069 111 Her A5III 4.36

7203 G6III 6.05

7217 o Sgr G9IIIb 3.77

7370 K4III 5.69

7388 K0-1III 6.13

7434 K0III 6.18

7536 M2II+A0V 3.82

7635 M0-III 3.47

7811 G6III 5.66

7813 K0III 6.41

7886 M6III 6.25

7903 A0III 6.08

7913 A7III 3.42

7934 K0III 5.41

7941 M5II-III 6.38

7968 K1II-III 5.05

8401 30 Aqr K0III 5.54

8618 40 Peg G8II 5.82

8660 45 Peg gG6 6.25

8929 K1III 6.02

9036 M2.5IIIb 5.08

Table 1: Stars of the input sample with less than 50 s exposure time or which are located in the region of the X-ray bright Vela supernova remnant

 

  
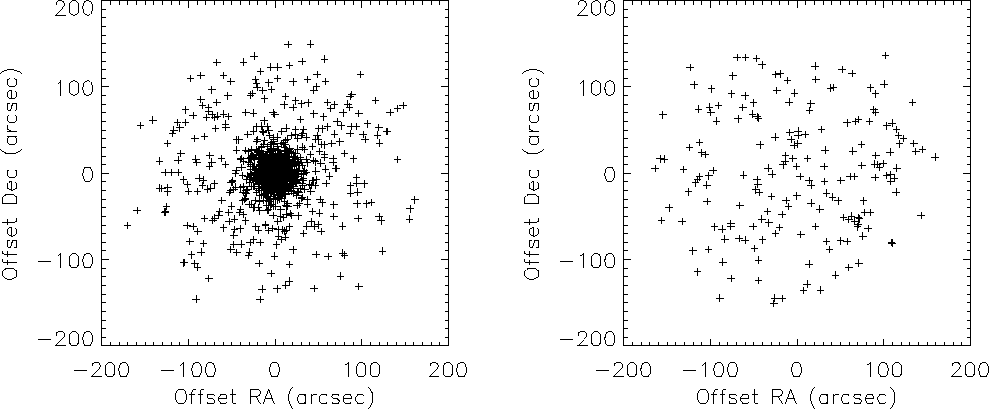
Figure 1: Distribution of offsets in RA and Dec between optical and X-ray position for matches of RASS sources with the whole BSC star sample (top) and with 10000 random sky positions (bottom)

2.3. Matches between input stars and RASS-sources

Our aim was to find X-ray sources detected in the RASS close to the positions of the input sample stars defined in the previous subsection. In the first step, we extracted all X-ray sources with a likelihood of in a square box of arcminutes dimension centered on the position of any (i.e., 9110) BSC stars. To find out up to what distance from the optically selected input positions an X-ray source can reliably attributed to a star, we proceeded as follows: We first constructed a sample of 10000 random sky positions by means of a Monte Carlo simulation. That sample was subjected to the same match procedure as the 9110 BSC positions. The two-dimensional distribution of the offsets in right ascension and declination between optical and X-ray positions is shown in Fig. 1 (click here) for both samples. The corresponding histogram of the offsets (in arcseconds) is plotted in Fig. 2 (click here), where the number of matches in each distance interval is normalized to the corresponding annular area, and where a correction factor due to the different numbers of input positions (i.e., 9110 vs. 10000) was applied. It is evident that for the BSC input sample the number of matches is strongly decreasing towards larger offset values, hence the vast majority of the obtained matches must be real. On the contrary, the similar number of matches for artificial sky positions is approximately independent of the offset distance (as expected), and has a more or less constant value of matches per square arcsecond. We further note that at an offset of arcseconds the number of artificial matches is about half the number of actual matches with BSC stars. That means, at that offset the (differential) probability of correctly identifying a BSC star with an X-ray source is about 50%.

Therefore, we chose 90 arcseconds as cut-off match distance between optical and X-ray position, up to which we attribute an X-ray source to a nearby BSC star.

  
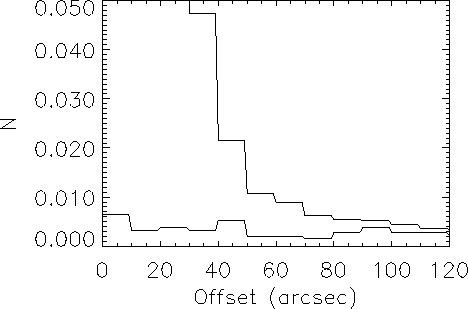
Figure 2: Histogram of offsets for the BSC star sample (upper line) and the random positions (lower line). The y-axis is given in numbers of matches within a given offset interval, divided by the area of the corresponding annulus

For about 200 X-ray sources extracted in this way and not included in the Bright Source Catalogue (Voges et al. 1996b), we checked the X-ray images by eye for reality. Specifically, we rejected photon distributions that are significantly contaminated by nearby strong sources or that are obviously extended. In questionable cases, we ran the standard source detection algorithm of EXSAS on the source images in different passbands and decided on the basis of the results which sources to retain in our final catalogue.

Confining now attention to the 3839 BSC positions identified with late-type giants and supergiants, we detected X-ray emission from 450 stars, i.e., the average detection rate is 11.7%. Since the total search area around these 3839 stars is 0.018% of the sphere, and the total number of RASS sources amounts to , we would expect 27.4 chance coincidences of late-type giants or supergiants with background (or foreground) X-ray sources (i.e., 6% of our detected sources). If we consider a maximum offset of 60 arcseconds, this would be even reduced to 12.2 chance coincidences. At least for one case, HR 4289, this has been verified (Hünsch et al. 1996b).

2.4. Determination of X-ray fluxes

The conversion of count rates (CR) into X-ray fluxes is generally performed by application of an energy-conversion-factor (ECF):

ECF depends on both the underlying X-ray spectrum of the source and the amount of interstellar hydrogen absorption. As the source spectrum can be assumed to be thermal emission from an optically thin plasma in the case of late-type stars, the main determining parameter is the temperature of the plasma. However, in addition to the general problems of determining spectral parameters from low-energy-resolution proportional counter measurements, the detailed analysis of X-ray spectra requires quite a large number of photons, i.e., bright sources or long exposure times. For most of the sources in our catalogue, these requirements are not fulfilled, thus their coronal temperatures are unknown. Moreover, information on the interstellar hydrogen column density is also lacking for most of the stars. For late-type stars, colour excesses are difficult to measure due to the large intrinsic scatter of the colour indices. On the other hand, giants are intrinsically bright objects, on average they are far away and the amount of interstellar absorption cannot be neglected in most cases.

Fortunately, a rough information on the energy distribution in the X-ray range is provided by the hardness ratio.

where H and S denote the source counts in the hard () and soft () passbands of ROSAT. The hardness ratio is an "X-ray colour'' that is influenced by both the plasma temperature and the hydrogen column density. Hünsch et al. (1996a) analyzed several PSPC pulse-height spectra of nearby giants and find from modelling the observed energy distributions by isothermal or two-temperature-component Raymond-Smith (1977) models a linear relation

Note that Schmitt et al. (1995) find a very similar relation for late-type main-sequence stars.

Since the SASS source detection was separately performed in both passbands, and since most of our X-ray sources were detected in both bands, the hardness ratios can be determined for most stars, although in some cases with quite large errors. In a few cases, where the sources were not detected in the soft passband, we set hr = +1.0 by definition. The error in the hardness ratio is given by

From the hardness ratios, we calculated individual energy-conversion-factors, which cover a range of . We refrain from estimating individual errors for since the error in ECF is very difficult to quantify. In general, we estimate the error to be within a factor of two for the weaker sources and less for the brighter sources.

Since the apparent flux depends on the distance, a more characteristic measure would be the X-ray luminosity . However, reliable distance measurements from parallaxes exist only for a minority of our sample stars. Spectroscopic parallaxes from luminosity classes are quite uncertain and absolute magnitudes from the Wilson-Bappu effect exist only for part of the stars brighter than . Therefore, we did not calculate individual X-ray luminosities. A distance-independent measure of the level of X-ray emission is the ratio of X-ray to bolometric flux. We calculated bolometric fluxes from the relation

where the apparent bolometric magnitude is given by . The bolometric corrections B.C. were taken from the tables of Schmidt-Kaler (1982) as given in the Landolt-Börnstein, by interpolating the values in colour index B-V and luminosity class whenever necessary. For the M-type stars, we used the spectral type instead of the colour index due to the weak dependence of B.C. on B-V.