Figure 2 (click here) shows a CMD of all 24999 stars that were identified independently on at least 4 frames. The V-I scale is so compressed by the occurence of very red stars that features like the horizontal branch are not easily recognizable. It is clear, however, that the dominant population is not the cluster but the field population of the Galactic bulge. To maintain good legibility by avoiding an inconvenient compression of the V-I scale, Fig. 5 (click here) plots only stars bluer than V-I =3.0. No selection with respect to photometric errors was done to maintain completeness. The full list of stars (Table 6 (click here)) is published in electronic form at CDS.
Figure 2: The colour-magnitude diagram shows all 24999 stars,
for which photometry could be obtained.
The V-I scale is strongly compressed by
the occurence of very red stars, so that the CMD features of the cluster
itself are hard to isolate. The cluster is embedded in a very rich population
of field stars, which is the main obstacle for a proper derivation of cluster
parameters.
Triangles are those stars redder than V-I = 3.0, which are closer
tha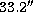n 
to the cluster center and accordingly have a high
probability of being cluster members. They show that the cluster is situated
in the foreground with respect to the red field star population
This CMD
shows why the investigation of this cluster is so difficult.
Practically all interesting structures in the CMD of NGC 6528 are contaminated
by the field population. While the horizontal branch (HB) can
be distinguished, the exact shape of the red giant branch (RGB) cannot
be clearly identified. OBB found strong differential reddening in the area
of NGC 6528 which further broadens the RGB and other features of the CMD.
Also a "tilted'' HB is recognisable, although less striking than
in other clusters like NGC 6553 (Subramaniam et al. 1997) or Terzan 5
(Grebel
et al. 1995).
The turn-off region is reached in our photometry. It is at
most 3.5 mag fainter than the HB, which is typical of old clusters
(e.g., Buonanno et al. 1989), but it is
completely hidden in the rich field. Here we skip any discussion of
the TO location due to the superior data of HST (Ortolani et al. 1995).
The problem now consists of properly selecting stars with a high
probability of being cluster members and statistically subtracting field
stars in order to isolate the significant features of the CMD.
A useful approach is to determine the radial distance beyond which the field
population starts to dominate over the cluster population.
A King model reads (King 1962)
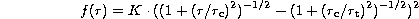
where K is the central stellar surface density (or surface brightness, respectively),
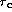the core radius and 
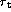the tidal radius.
Webbink (1985) quotes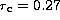 
arcmin and 
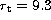arcmin, while
Trager et al. (1993) give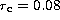 
arcmin and 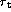= 16.6 arcmin. These differences illustrate the
difficulties of deriving structural parameters for a cluster so strongly
embedded in the field population. Our attempts to fit a King profile confirmed
the degeneracy of the parameters. However, our area is quite
limited so we cannot improve the parameter values.
We determined the radial profile of
the surface density, selecting stars brighter than V = 19 mag, where we are
complete except perhaps for the very center. We find for the central surface
density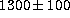 
stars/square arcmin. The observed density profile
together with two King models with the above parameters
are given in
Fig. 3 (click here). From this plot, the cluster and field
densities are equal at a radius 1.1 arcmin. At 2.5 arcmin, the field density
is already 8 times higher than the cluster density in case of the
Trager et
al. (1993) model.
The CMD of the field population (Fig. 4 (click here))
therefore consists of stars with radial distances larger than 2.5 arcmin.
Figure 3: This plot shows the observed stellar
surface density (logarithm of stars brighter than V=19 mag per square arcmin)
as a function of radius (triangles). Also plotted are two King models with
parameters quoted by Webbink (1985, solid line) and
Trager et al. (1993,
dotted line). At a radial distance of about 1.1 arcmin,
the field population equals the cluster population. For constructing the
field CMD, one should select stars with radial distances larger than 2.5
arcmin, where the cluster population is negligible
Figure 4: The CMD of the field population around NGC 6528. We
selected stars with radial distances larger than 2.5 arcmin to plot this
diagram.
Triangles are those stars redder than V-I = 3.0, which are closer
than 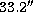to the cluster center and accordingly have a high
probability of being cluster members.
One recognizes that the giant branch of NGC 6528 constitutes a brighter envelope to this
star distribution and thus is located in the foreground
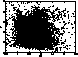
Figure 5:
This plot shows the CMD in V, V-I of the NGC 6528 region containing
only stars bluer than V-I = 3.5. It is obvious that this diagram is
overwhelmingly dominated by the population of the Galactic bulge. The
HB of the cluster is discernible while the RGB
cannot be clearly identified. The turn-off region is reached in our
photometry but the turn-off itself is completely hidden in the field
population
The location of the RGB is the basis for estimation of the metallicity and reddening. In Fig. 5 (click here), it is difficult to locate the cluster RGB among the numerous field stars. We found that statistical field star subtraction in the region of the RGB does not give useful results due to small number statistics. Selection according to distance from the cluster worked much better.
We found that selecting the stars with distances less than 100 pix (0.553 arcmin) gave the best representation of the RGB. We are using this selection to define a fiducial for the RGB and the HB (both given in Fig. 6 (click here)). Numerical values of the adopted fiducial are presented in Table 7 (click here).
It is interesting to note that the "tilt'' of the HB recognizable
in Fig. 5 (click here) vanishes in Fig. 6 (click here). Such tilts
have been repeatedly reported for metal-rich clusters.
Armandroff
(1988) proposed differential reddening as the cause, because the slope
of the tilted feature resembles in the most striking cases the reddening
vector. OBB already remarked that the HB gets more clumpy when HB stars
near the cluster center are considered, which is confirmed by Fig. 5 (click here).
This means that the tilt is mainly due to differential reddening in the field
population.
On the other hand, NGC 6553 (Ortolani et al. 1991;
Subramaniam
et al. 1997) and Terzan 5 (Grebel et al. 1995) are examples, where the tilted HB branch
is seemingly not induced by a smooth reddening gradient in the cluster field,
but rather by extremely patchy reddening. This conjecture is strengthened by the
fact that the "tilted'' HB is more striking with increasing foreground reddening.
However, a deeper discussion must include better data of highly reddened clusters.
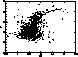
Figure 6:
CMD resulting from a selection with of stars closer than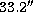
to the cluster center. This selection was used to define a fiducial for
the RGB and the HB, which is overplotted (filled
circles). It can be seen that the apparent "tilt'' of the HB,
which may be present in Fig. 2 (click here) vanishes if the stars
on the HB have a high probability of being cluster members
| V-I | V |
| 2.909 | 15.489 |
| 2.645 | 15.672 |
| 2.309 | 16.120 |
| 2.151 | 16.486 |
| 2.003 | 16.818 |
| 1.887 | 17.317 |
| 1.835 | 17.616 |
| 1.787 | 17.998 |
| 1.719 | 18.663 |
| 1.640 | 19.410 |
| 1.645 | 19.826 |
| 1.592 | 20.125 |
| 1.661 | 17.217 |
| 1.698 | 17.217 |
| 1.719 | 17.217 |
| 1.740 | 17.217 |
| 1.761 | 17.217 |
| 1.745 | 17.234 |
| 1.724 | 17.234 |
| 1.703 | 17.234 |
| 1.692 | 17.234 |
Figure 2 (click here) shows many very red stars, the reddest ones have V-I = 7. They cannot be late M dwarfs since they are preferably found among the brighter stars, so they should be intrinsically bright. OBB interpret their occurence as a continuation of the RGB, caused by the high metallicity of the cluster and suggest that these stars are affected by strong blanketing.
The cluster membership of these stars is naturally of interest. If giants with such red V-I colours occur in metal rich populations, we expect these stars to be present among to the Galactic bulge field stars as well. Indeed, the large majority of the stars redder than V-I = 3.5 does not show any concentration towards the cluster center and therefore likely belong to the bulge population.
However, a subsample have a high probability of being cluster
members, since a selection according to
radial distance (less than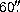 
from the cluster center) is equivalent to
the selection of the outer envelope of the distribution of the red stars (see
Fig. 4 (click here)).
This implies that the cluster is not embedded in the field population,
but is located in the foreground.
Garnavich et al. (1994) found a "curved giant branch'' in the V-I,
V-diagram
of NGC 6791, a metal-rich old open cluster. Their calculations show that the decreasing V
brightness can be understood simply as a consequence of a
rapidly increasing bolometric correction. Quantitative theoretical
statements concerning colours are difficult to make, since no detailed atmospheric models
exist for very cool giants (c.f. Gustafsson & Jørgensen 1994),
but models for cool dwarf stars show that already in the black or
grey body approximation the stellar continuum at or below temperatures
of 3000 K easily produces colours as red as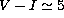 
.
In Fig. 7 (click here) a theoretical isochrone from Bertelli et al. (1994)
is overplotted. The isochrone has Z=0.02 and an age of 13.2 Gyr. The solid
line is the RGB while the filled circles trace the AGB. It turns out that,
if the reddest stars are indeed cluster members, the discrepancy between the
theoretical isochrone and the actually observed locus starts at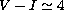 
.
The evolutionary status of the red stars is not clear, but one may suspect
in analogy to the theoretical isochrones that they are on the AGB rather than
on the
RGB.
To assess at least roughly their effect on integrated colours, we first calculate an integral V-I
colour of all stars in Fig. 2 (click here) and get 1.82 mag, while omitting the
stars with V-I > 3.5 (as in Fig. 5 (click here)) results in an integrated
colour of 1.70 mag. This effect is plausibly even stronger in the infrared. So
this red extension of the AGB/RGB stars must be taken into account, when modelling
spectra of elliptical galaxies. See the contributions by Bruzual (1996),
Worthey
(1996), Chiosi (1996) for a deeper discussion of related problems.
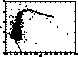
Figure 7: This plot shows the full colour range of stars with
the selection of being closer than 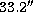to the cluster center.
Overplotted is a theoretical isochrone from
Bertelli et al. (1994) with an
age of 13.2 Gy and solar metallicity, including the Red Giant Branch (RGB,
solid line)
and
the Asymptotic Giant Branch (AGB, filled circles). While the isochrone traces the RGB and the AGB well to 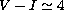, they deviate at redder colours and
also do not cover the full extension of the CMD. Whether
the reddest stars are RGB or AGB stars, is unclear
The question for the age of NGC 6528 is of high importance for
the metal-rich bulge population of which NGC 6528 is
a representative.
Is NGC 6528 placed among those few globular clusters
that are younger than the bulk of clusters, like Pal 12
(Gratton & Ortolani
1988) or Ruprecht 106 (Buonanno et al. 1990)? That "disk'' clusters may
be younger than halo clusters has been suggested for instance by
Richtler
et al. (1992) and Hatzidimitriou (1991).
Ortolani et al. (1991) cited
NGC 6553 as possibly younger. However, Richtler et al. (1994) showed that
three other clusters, which had been classified
as disk clusters (but in fact have properties more consistent with halo
clusters), could not be distinguished in age from the bulk of
globular clusters.
After the first version of this paper had been submitted,
Ortolani et al.
(1996)
published a CMD of NGC 6528, based on HST-data (WFPC2). Although the present data
are the deepest so far obtained from the ground for NGC 6528, they are definitely
less reliable concerning the turn-off location due to the strong crowding at the
relevant magnitude level. Therefore we renounce a deeper
discussion and simply refer to Ortolani et al. who found that NGC 6528 is
indistinguishable in age from the metal-poorer clusters in the galactic halo.
Sarajedini (1994) devised a simple method to derive metallicity and reddening
simultaneously from a V, V-I diagram by using two metallicity indicators,
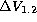, the magnitude difference between HB and RGB at the
unreddened V-I colour 1.2, and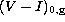 
, the (unreddened) V-I colour
of the RGB at the HB magnitude level. These metallicity indicators depend
in different ways on the reddening. Thus we can regard reddening and metallicity
to be determined, if both indicators give the same metallicity for the same
reddening. However, a direct application is not possible since in
Sarajedini's calibration, 47 Tuc appears with -0.7 dex as the most
metal-rich cluster, whereas one wants to have a calibration extended to at
least solar metallicity.
At present this is practically impossible to do in a purely empirical way. There are simply no V, V-I CMDs for clusters suitable for inclusion in the metal-rich domain as a supplement to Sarajedini's calibration. But there are also only a few theoretical isochrones available for clusters this metal-rich. The only published V-I isochrones for old and metal-rich clusters that we are aware of are those of Tripicco et al. (1995) and from Bertelli et al. (1994). Our approach is therefore to use these isochrones like empirically determined CMD loci and supplement the calibration set of Sarajenini.
The 12 Gyr, solar metallicity isochrone of
Tripicco et al. (1995) agrees very well
with a
linear extrapolation of Sarajedini's relations and its inclusion has
only a little effect on the coefficients. For this
isochrone,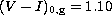 
and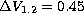 
. Measuring these
indicators, we adopted for the brightness of the HB MV = 1.05 mag, as
indicated by the red part of the theoretical HB of Tripicco et al. (1995).
A linear regression then leads to
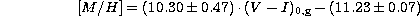
and
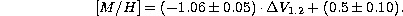
These relations can now be used individually to plot reddening against
metallicity, using the proper values for NGC 6528, for which we adopted
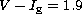and the numbers given in Table 8 (click here). These two
lines then intersect at a certain pair of values that
we regard to be the cluster reddening and metallicity.
It is apparent that the main uncertainty is introduced by
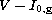, which loses sensitivity in the metal-rich domain. We conclude
from this method that the reddening of NGC 6528 is E(V-I) = 0.8
and a metallicity of
.
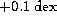| V-I |  |
| 2.62 | 0.06 |
| 2.72 | 0.39 |
| 2.80 | 0.64 |
| 2.95 | 1.00 |
| 1.16 | 1.16 |
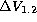for different values
of the reddening
If Sarajedini's relation is supplemented with the aid of the Bertelli et al. (1994) isochrones, the linearity is lost and a significant curvature is introduced. We chose the [13.2 Gy, Z=0.02] isochrone for extrapolating to solar metallicity.
For this isochrone,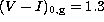 
and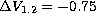 
.
Including this point in Sarajedini's relation,
leads to
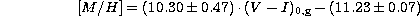
and
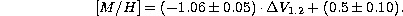
Applying the above relations, our result for reddening and metallicity is E(V-I) = 0.6 and [M/H]=-0.4 dex. The uncertainty expressed by this difference can presently not be avoided.
 |  |  | [M/H] (T) |  | [M/H] (B) |
 |  | 0.8 | +0.1 dex | 0.6 | -0.4 dex |
Calculating the distance based on HB brightness, we have to adopt a relation between brightness and metallicity for HB stars (basically for RR Lyrae stars). A recent compilation of related work has been given by Chaboyer et al. (1996). Their preferred relation is
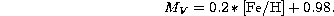
To span a representative range of values occurring in the literature, we
also adopted the relation favoured by Nemec et al. (1994):
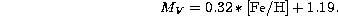
Moreover, the absorption depends on the colour of the star considered. Assuming
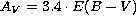(Grebel & Roberts 1995) as the appropriate relation
for our value of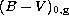 
, and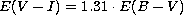 
, we get
the values for MV(HB), absorption, distance modulus and corresponding
distance listed in Table 10 (click here). This table shows the full dilemma
of distance determination of reddened globular clusters.
We note that the ration AV/E(B-V) might also be discussed. In case of NGC 6528, a change of 0.3 would cause a shift of 0.25 mag in the distance modulus.
Formally, there is
no hard reason to consider any of these values as being more reliable than
the others. However, since the structure of the CMD sets the cluster in
the foreground, the high values are not probable. The recent investigation
by Fusi Pecci et al. (1996) of M 31 globular clusters argues in favour of the
Chaboyer et al. relation, so the distance value of 6.6 kpc might be preferred.
One notes that
the external error is much more dependent on the uncertain metallicity,
absorption and HB brightness than on the photometric errors.
| E(V-I) | 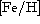 | MV(HB) | AV | m-M | D[kpc] | z[kpc] |  |
| 0.8 | +0.1 | 1.22 (N) | 2.08 | 13.91 | 6.0 | 0.4 | 2.0 |
| 0.8 | +0.1 | 1.02 (C) | 2.08 | 14.11 | 6.6 | 0.5 | 1.5 |
| 0.6 | -0.4 | 1.06 (N) | 1.55 | 14.60 | 8.3 | 0.6 | 0.7 |
| 0.6 | -0.4 | 0.90 (C) | 1.55 | 14.76 | 8.9 | 0.7 | 1.1 |