The zodiacal light is given in terms of ecliptic coordinates

with the zero point of

in the Sun. Description of a line of sight by elongation

and inclination i also is common. For the relation between these two sets of coordinates see Fig. 2 (click here) and Sect. 3.5 (click here) below.
Integrated starlight is naturally presented in galactic coordinates l,b.

For estimates of the diffuse background brightness at a given position, transformation between these three systems is necessary. Figures 3 (click here)-7 (click here) provide a simple way to do so graphically with about one-degree accuracy, which is sufficient for many applications. The underlying transformation equations are summarised below for ease of access.

Airglow, extinction and scattering are best described in the local horizontal system A, z (azimuth, zenith distance). The transformation to the other systems depends on time and on the observer's geographic coordinates. For the horizontal system, only the equations for the transformation to the equatorial system are given.

3.1. Ecliptic and equatorial coordinates

The obliquity of the ecliptic is essentially constant,

= 23.446

for equinox 1950, respectively

= 23.439

for equinox 2000.

The precession of the vernal equinox along the ecliptic is p₀ = 50.3 ''/year. Hence

The north ecliptic pole is at

= 18 h,

.
The north celestial pole is at

Both

and

are counted eastward from the vernal equinox. Apart from the minimal change in

, the transformation equations then are the same for 1950 and 2000:

3.1.1. Transformation

3.1.2. Transformation

3.2. Galactic and equatorial coordinates

By IAU decision, for equinox 1950 the north galactic pole (NGP) is at

= 12 h 49.0 m,

= 27.4

and the celestial pole at l = 123.0

, b = 27

24.0'. Hence the ascending node of the galactic equator is at

= 18 h 49.0 m = 282.25

= 33.0

. For equinox 2000, the coordinates of the north galactic pole are

= 12 h 51.42 m,

= 27

07.8', and we have

= 282.86

= 32.93

. The inclination of the galactic equator with respect to the ecliptic is

. As

and

, l is also counted eastwards.

3.2.1. Transformation

3.2.2. Transformation

3.3. Galactic and ecliptic coordinates

In ecliptic coordinates, for equinox 1950 the north galactic pole is at

= 179.32

= 29.81

, and the ascending node of the galactic equator at

= 269.32

, l₁ = 6.38

. For equinox 2000, the coordinates of the north galactic pole are

= 180.02

= 29.81

, and we have

= 270.02

, l₁ = 6.38

. The inclination of the galactic equator with respect to the ecliptic is

. As already mentioned, l is counted eastwards. With these parameters, the transformations are as follows:

3.3.1. Transformation

3.3.2. Transformation

3.4. Altazimuth and equatorial coordinates

The transformation depends on local sidereal time

and on geographical latitude

. Instead of elevation, zenith distance z = will be used. The zenith distance of the celestial pole is

. Both, azimuth A and hour angle

are counted from the meridian through west.

3.4.1. Transformation

3.4.2. Transformation

3.5. Alternate ecliptic coordinates

Instead of

also a sun-centered polar coordinate system is used. Its coordinates are the angular distance from the sun, called elongation

, and a position angle i, counted from the ecliptic counterclockwise,called inclination. The relation between the two sets of coordinates, when describing the position of a field-of-view with respect to the sun, is shown in Fig. 2 (click here).
It is unfortunate that the obliquity of the ecliptic, used in Eqs. (3 (click here)) and (4 (click here)), and the angular distance from the sun, used in Eqs. (11 (click here)) and (12 (click here)), both are designated by the same letter

. However we did not want to change the commonly used notations. In practice this dual meaning rarely should lead to confusion.

Figure 2: Relation between the coordinates used for presenting zodiacal light measurements.

is counted positive towards east, i is counted positive counterclockwise from the ecliptic west of the Sun

3.5.1. Transformation

3.5.2. Transformation

The reader is cautioned that in some papers the differential helioecliptic longitude

may be called "elongation" or may be designated as "

", contrary to our definition of elongation

as the angular distance from the sun to the field-of-view.

Figure 3: Relation between coordinates (lines) and (underlying dotted grid) for equinox 2000

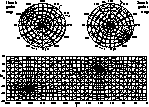
Figure 4: Relation between coordinates (lines) and l, b (underlying dotted grid) for equinox 2000

Figure 5: Relation between coordinates l, b (lines) and (underlying dotted grid) for equinox 2000 - alternative projection

Figure 6: Relation between coordinates (lines) and l, b (underlying dotted grid) for equinox 2000

Figure 7: Relation between coordinates l, b (lines) and (underlying dotted grid) for equinox 2000 - alternative projection

Site	I_B(max)	I_B(min)	I_V(max)	I_V(min)	Solar flux	Corresponding dates	ref.
ESO	22.74		21.69		164	78-02-05	1.
	(22.20)		(20.85)		168	80-12-06; 80-06-08; 88-12-05
		22.97			161	78-02-08
		(22.94)			116	78-02-08; 87-12-16; 87-12-19;
				21.91	162	78-02-07
				(22.02)	94	87-12-15; 87-12-16; 87-12-19;
Calar Alto	22.51(22.30)				61	95-05-26,27,28	2.
		23.05(22.98)			176	89-05-06; 90-06-26; 93-06-21
			(21.16)		206	89-05-04; 91-06-11; 91-06-16
				21.79	61	95-05-27,28,29
San Benito Mt.	22.37		21.32		233	80-04-11; 81-07-28; 82-06-22	3.
		23.08			78	76-04-30; 87-04-25; 87-06-29
				22.07	76	76-04-30; 87-04-28; 87-06-29
Kitt Peak	22.65				114	88-01-21; 88-03-17; 88-06-14	4.
		22.98			75	86-12-02; 86-12-30; 87-06-22
			21.60		114	87-11-20; 88-03-17; 88-06-14
				22.01	75	86-12-02; 86-12-31; 87-06-22
Crimea	21.91		21.10		122	68-04-28; 71-04-25; 70-08-09	5.
		23.05		22.05	136	68-03-29; 68-04-06; 68-04-28
Hawaii	22.27				210	88-11-13; 89-03-28; 89-09-12	6.
		23.03			142	87-08-26; 87-11-13; 89-06-10
			21.21		166	85-12-13; 88-11-13; 89-03-28
				22.05	102	86-06-02; 87-08-26; 88-07-18
McDonald	22.54		21.54		138	60-02-04; 72-12-30; 73-01-12	7.
Observatory		23.01			156	60-01-27; 72-01-11; 72-01-15
				21.92	159	60-01-27; 72-01-15; 73-01-08
1. Mattila et al. (1996a).
2. Leinert et al. (1995), Leinert et al. (1996, unpublished).
3. Walker (1988).
4. Pilachowski et al. (1989).
5. Lyutyi & Sharov (1982).
6. Krisciunas (1990).
7. Kalinowski et al. (1975).

Table 4: Comparison of B and V zenith sky brightnesses at different sites in units of mag/

''. The minimum/maximum values given are averages of the three smallest/largest sky brightness values (nightly averages) given for each site. In the case of ESO and Calar Alto, the numbers in boldface refer to actual B, V measurements, while the numbers in parantheses have been transformed from medium band filter measurements. The given solar 10.7 cm flux value (in units of 10⁴ Jy) is the average of the three nights in question