A typical number of 6000 specklegrams are read from the video tapes for each
object (binary star and reference star). For faint objects (mag ![]() 9)
this number can reach 15000. Frames are digitized within a square sub-image
of the video field. The size of this sub-image is generally 128
9)
this number can reach 15000. Frames are digitized within a square sub-image
of the video field. The size of this sub-image is generally 128![]() 128
or 256
128
or 256![]() 256, depending on the star separation and the size of the
long-exposure image. The total size of the video field is 384
256, depending on the star separation and the size of the
long-exposure image. The total size of the video field is 384![]() 288.
Each video grab is then checked for bad points, null images and loss of
video synchronization signal. Images showing these features are deleted.
288.
Each video grab is then checked for bad points, null images and loss of
video synchronization signal. Images showing these features are deleted.
During the observation of a star, seeing conditions may change and images
are classified according to the strength of turbulence before processing.
This classification is performed the following way. The square modulus of
the Fourier transform of each specklegram is computed. An instantaneous
Fried parameter r0 is estimated by fitting the low-frequencies of this
energy spectrum with a Kolmogorov spectrum (Fried 1966;
Roddier 1981):
![]()
where f is the spatial frequency and ![]() the wavelength. After each
specklegram is associated to a Fried parameter, images are binned into 5
classes according to image quality: class 5 contains the best images (low
turbulence, good visual quality), class 1 the worst.
Figure 1 (click here) gives an illustration of typical frames in each
class. The processing of the data is made separately for each class. The
classes we have processed are mainly classes 3 and 4 since the number of
images belonging to class 5 was often too low (10-40).
the wavelength. After each
specklegram is associated to a Fried parameter, images are binned into 5
classes according to image quality: class 5 contains the best images (low
turbulence, good visual quality), class 1 the worst.
Figure 1 (click here) gives an illustration of typical frames in each
class. The processing of the data is made separately for each class. The
classes we have processed are mainly classes 3 and 4 since the number of
images belonging to class 5 was often too low (10-40).
![]()
Figure 1: Classes of specklegrams illustrated with the star c Her. From
left to right: classes 1 to 5. The field of view is ![]() . From a total number of 4999 frames of c Her digitized from the tape,
the class repartition was the following. Class 1: 468 images, class 2: 2979
images, class 3: 1350 images, class 4: 191 images and class 5: 11 images. On
the best images (class 5), the double star can sometimes be seen directly on
the specklegrams
. From a total number of 4999 frames of c Her digitized from the tape,
the class repartition was the following. Class 1: 468 images, class 2: 2979
images, class 3: 1350 images, class 4: 191 images and class 5: 11 images. On
the best images (class 5), the double star can sometimes be seen directly on
the specklegrams
The separation ![]() is derived from the autocorrelation function. The
power spectrum of both the double star and the reference star are computed
for a given image class. The visibility function is obtained by dividing the
two power spectra. An apodisation is then made by multiplying the visibility
function by a transfer function of a circular telescope. The Fourier
transform of the result gives the autocorrelation of the double star
corrected from the turbulence. For a binary star, this function shows a
central peak and two lateral ones. The distance between the central peak and
the lateral ones gives the star separation. In practice we computed the
photocenter of the lateral peaks on a 5
is derived from the autocorrelation function. The
power spectrum of both the double star and the reference star are computed
for a given image class. The visibility function is obtained by dividing the
two power spectra. An apodisation is then made by multiplying the visibility
function by a transfer function of a circular telescope. The Fourier
transform of the result gives the autocorrelation of the double star
corrected from the turbulence. For a binary star, this function shows a
central peak and two lateral ones. The distance between the central peak and
the lateral ones gives the star separation. In practice we computed the
photocenter of the lateral peaks on a 5![]() 5 grid centered on the peak
maximum. The error bar is obtained by differentiation of the formula used
for photocenter determination, the noise being estimated in a 10
5 grid centered on the peak
maximum. The error bar is obtained by differentiation of the formula used
for photocenter determination, the noise being estimated in a 10![]() 10
grid located far from the central and the lateral peaks. The accuracy
depends on various parameters such as seeing conditions, magnitude
difference, and total magnitude of the binary star and the reference star.
The 1994 measurements (oversampled images) were more precise (typical errors
3 mas) than the 1995 ones (typical errors 15 mas).
10
grid located far from the central and the lateral peaks. The accuracy
depends on various parameters such as seeing conditions, magnitude
difference, and total magnitude of the binary star and the reference star.
The 1994 measurements (oversampled images) were more precise (typical errors
3 mas) than the 1995 ones (typical errors 15 mas).
Absolute position angles (i.e. containing the quadrant information) were computed using the recent technique of cross correlation (Aristidi et al. 1996) which is currently under development at the Département d'Astrophysique of Nice University. This technique consists of computing the ensemble average of the cross-correlation between the specklegrams and their square. In practice the computation is made in the Fourier plane: the cross spectrum between the specklegrams and their square is obtained both for the double star and the reference star. It is a complex quantity whose imaginary part contains the absolute quadrant information. The cross-spectrum of the double star is then divided by those of the reference star. An apodizing function (transfer function of a circular telescope) is applied and a Fourier transform is made. Although the result looks very similar to the autocorrelation (a central peak and two lateral ones), the lateral peaks of the cross-correlation are asymmetric. As presented in Fig. 2 (click here) for several binaries, this asymmetry gives the absolute position of the companion.

Figure 2: Gray-level plots of cross-correlations computed on the specklegrams
of six binary stars. This function shows a central peak surrounded by two
smaller asymmetric ones. The asymmetry of the secondary peaks gives the
orientation of the couple, the distance between lateral peaks and the
central one provides the angular separation. The look-up table used for this
representation is drawn on the right. Scale and orientation are indicated at
the top of each picture. The case of ![]() Cyg is interesting: due to the
large magnitude difference of the couple (
Cyg is interesting: due to the
large magnitude difference of the couple (![]() ), only one of the
lateral peaks is visible, the second one being in the noise
), only one of the
lateral peaks is visible, the second one being in the noise
The relative photometry of the system is obtained by using ratios of twofold
probability density functions (Carbillet et al.
1996b). The twofold probability density function (PDF)
is a function of two random variables of intensity (![]() and
and
![]() ), and a space-lag
), and a space-lag ![]() . Whatever the value of
. Whatever the value of ![]() , the
twofold PDF for a point-source (a non-resolved reference star) has a
symmetrical structure in
, the
twofold PDF for a point-source (a non-resolved reference star) has a
symmetrical structure in ![]() and
and ![]() . For
. For ![]() close to
the separation vector
close to
the separation vector ![]() between the two components, the twofold
PDF for a binary star has an arrow-head shape with a trend towards a
direction
between the two components, the twofold
PDF for a binary star has an arrow-head shape with a trend towards a
direction ![]() of the order of
of the order of ![]() , where
, where ![]() is the
oriented intensity ratio. The direction
is the
oriented intensity ratio. The direction ![]() is
tremendously enhanced by dividing the twofold PDF of the binary star,
computed for
is
tremendously enhanced by dividing the twofold PDF of the binary star,
computed for ![]() , by the twofold PDF of the reference
star, computed for the same space-lag
, by the twofold PDF of the reference
star, computed for the same space-lag ![]() . The resulting quantity,
the so-called function Q, clearly shows a ridge that simply follows:
. The resulting quantity,
the so-called function Q, clearly shows a ridge that simply follows:
![]() . The oriented intensity ratio
. The oriented intensity ratio ![]() can then be
easily evaluated by doing a radial integration of
can then be
easily evaluated by doing a radial integration of ![]() :
:
![]() , where
, where ![]() is the angle measured in polar coordinates in
the
is the angle measured in polar coordinates in
the ![]() plane. The function Q-QT, where QT is the
transposed quantity of Q, can also be computed in order to enhance the
relevant ridge. In that case, the radial integration gives both
plane. The function Q-QT, where QT is the
transposed quantity of Q, can also be computed in order to enhance the
relevant ridge. In that case, the radial integration gives both ![]() (corresponding to the maximum of IQ-QT), and
(corresponding to the maximum of IQ-QT), and ![]() (corresponding
to the minimum of IQ-QT). The error bars are then derived from a
binomial fit of the regions close to the extrema of the radial integration,
since a convex function has a quadratic behavior close to its extrema.
(corresponding
to the minimum of IQ-QT). The error bars are then derived from a
binomial fit of the regions close to the extrema of the radial integration,
since a convex function has a quadratic behavior close to its extrema.
An alternative quantity may be used when no reference star is available: the
division of the twofold PDF computed for ![]() by the
twofold PDF computed for
by the
twofold PDF computed for ![]() .
.
Figure 3 (click here) shows the functions Q-QT (and their radial integrations) computed for three different type of data.

Figure 3: Gray-level plots of function Q-QT, and plots of its radial
integration IQ-QT, computed on the specklegrams of three binary stars.
The radial integrations show two extrema. The maximum is reached for
![]() , the minimum for
, the minimum for ![]() ,
, ![]() being the
intensity ratio of the two binary components. A value of
being the
intensity ratio of the two binary components. A value of ![]() means
that the spatial lag vector goes from the brightest star to the lowest. The
opposite if
means
that the spatial lag vector goes from the brightest star to the lowest. The
opposite if ![]() . This gives the absolute position angle of the
couple
. This gives the absolute position angle of the
couple
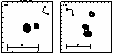
Figure 4: Restored images of ![]() Del (a) and 2 Cam (b). These
images were computed from 212 specklegrams (class 5) of
Del (a) and 2 Cam (b). These
images were computed from 212 specklegrams (class 5) of ![]() Del and 1162
specklegrams (class 4) of 2 Cam. The image restoration procedure is
described in Sect. 3.5
Del and 1162
specklegrams (class 4) of 2 Cam. The image restoration procedure is
described in Sect. 3.5
We have restored images of ![]() Del and 2 Cam (Fig. 4 (click here))
using the bispectral method described in Lannes (1988) and
Prieur et al. (1991).
Del and 2 Cam (Fig. 4 (click here))
using the bispectral method described in Lannes (1988) and
Prieur et al. (1991).
The mean bispectrum and power spectrum were computed from the elementary frames of the same class (cf. Sect. 3.1). The phasor of the spectrum was derived from that of the mean bispectrum phasor through a global least-square minimization inversion method as described by Lannes (1988). This resulting phasor associated with the modulus of the spectrum derived from the mean power spectrum leads to an image which was then deconvolved by a Point Spread Function (PSF) obtained by observing a reference star (cf. Sect. 2). The deconvolution method we used (Lannes et al. 1987a, b) preserves the photometry, which allowed us to perform photometric analysis of the restored images. The measurements of the intensity ratios (taking the brightest component as a reference) lead to: