As we have seen, the Medium-Range and Local Area prediction models may actually provide a set of predicted weather related parameters which could support an attempt to active scheduling of the observations. And the atmospheric mesoscale numerical prediction may be a key approach to seeing nowcast too, when service observing scheduling is needed (Bougeault et al. 1995). Nevertheless, the absolute errors which are shown by operational high resolution prediction models are much higher than the astronomical constraints. Moreover, the computing and human resources which are required for developing, servicing and operating Local Area Models gives them a very low flexibility.
Medium-Range and Local Area prediction models require a closed set of appropriate physical laws expressed in mathematical form, suitable initial and boundary conditions and an accurate numerical method of integrating the system of equations forward in time. Within the framework of a very short time range prediction, several different methodological approaches can be investigated, which do not require the knowledge of underlying physical laws. A standard black box configuration, where an input set of data is being processed and an output result is produced, can be a correct layout for our purposes.
Neural networks mime a black box model: this is accomplished using time series of meteorological parameters as an approach to forecast dynamical processes. Murtagh & Sarazin (1993) approached the temperature and seeing prediction by using a neural network model. A similar approach has been used here for temperature prediction as a feasibility study in support of a generic dome thermal environment control system. The neural network is a non linear approach to data series treatment which is highly flexible, presents a low-cost from the computing point of view and may provide excellent results.
A Neural Network (NN) (e.g. Hecht-Nielsen 1991; Hertz et al. 1991) is a flexible mathematical structure which is capable of identifying complex non-linear relationships between input and output data sets. For these reasons NN models have been found useful and efficient, particularly in problems for which the characteristics of the process are difficult to describe using physical equations. NN are powerful objects having inference and generalisation capabilities; in fact, a NN which has been trained with a representative number of examples of a given process is able to extrapolate states not present in example data set.
The network topology we chose is the usual feed forward (FF) (Fig. 1 (click here)a), which has been found to have high performances in input-output function approximation (Elsner 1992). In a typical three-layer FF NN
Figure 1: The a) draw shows a three-layers feed forward neural net.
A processing unit element is drawn in b)
the first layer connects the input variables and is called the input layer.
The last layer connects the output variables and is called the output layer.
Layers in-between the input and output layers are called hidden layers; there
can be more than one hidden layer. The processing unit elements are called nodes
(Fig. 1 (click here)b): each of them is connected to the nodes of neighbouring
layers. The parameters associated with each of these connections are
called weights. All connections are "feed forward''; that is, they allow
information transfer only from an earlier layer to the next consecutive
layers. Nodes within a layer are not interconnected, and nodes in non
adjacent layers are not connected. Each node j receives incoming signals
from every node i in the previous layer. Associated with each incoming
signal xi is a weight wji. The effective incoming signal sj to
node j is the weighted sum of all incoming signals:
where x0=1 and wj0 are called the bias and the bias weights,
respectively. The effective incoming signal, sj, is passed through a non-
linear activation function (called also transfer function or threshold function)
to produce the outgoing signal (hj) of the node. The most commonly used
activation function is the sigmoid function. The characteristic of a sigmoid
function is that it is bounded above and below, it is monotonically increasing,
and it is continuous and differentiable everywhere. The sigmoid function we used
is:
in which sj ranges from 
to 
, but hj is bounded between
-1 and 1. In our scheme only signals processed in hidden units are passed
through the activation function.
To achieve weights optimisation a large number of "training'' algorithms exists, each of which is characterised by a learning law that will drive the weight matrix to a location that yields the desired network performance. Due to its rapid convergence properties and robustness, we chose a Levenberg-Marquardt algorithm (Nørgaard 1995) as engine in the minimization procedure.
In order to avoid overfitting, the network's performances are usually measured using two different data set: the training set and the validation set. While the training set is used directly to train the network, the validation set is used only for the evaluation process. Another way to increase network's performances consists in removing of idle connections (pruning): one of most popular method is the so called "brain damage'', which needs a retraining after each trial unit damage.
The temperature data series we used come from the Carlsberg Automated Meridian
Circle (CAMC) automatic weather station, which provides several meteorological
parameters with a 5 minutes time interval. The meteorological transducer for
temperature monitoring is an AD590K, which can operate from -55 to 
; it is positioned on a mast head at 10.5 metres above
ground. In this paper the CAMC site is supposed to be representative of the
temperature variations which can be found at the ORM, where both CAMC and
TNG are operated.
In this paper we present a preliminary study of temperature forecast at ORM site using linear and non-linear autoregressive models.
These statistical models based on the original idea due to Box and Jenkins (BJ) represent the fundamental approach in system identification and time series studies since the early '70s (Box & Jenkins 1970). The basic idea of BJ approach is that if a system is (partially) governed by deterministic rules, the future behaviour may be in some extent modelled from the behaviour of the past states.
The classic linear autoregressive moving average with exogenous inputs
(ARMAX) approach consists in modelling the (deterministic part of a) generic
variable of time T(t) at time 
(in our case
T is the temperature) by the function T'(t) defined as:
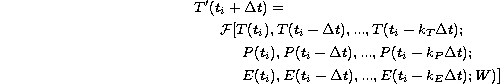
where 
is a linear function (linear combination), T, P and E
are the vectors containing the fitting regressors, W is a vector
containing the weights of the linear combination, 
is the time
lag and kT, kP and kE are the number of past regressors used for
each estimation. E(ti) = T(ti) - T'(ti) is a recurrent (dynamic)
term containing error (noise) propagation estimation. In our case we choose
pressure as exogenous variable P. The choice of pressure has been
suggested by an analysis of the cross-correlation structure between
temperature and all the others meteorological variables collected by CAMC.
The exogenous regressor P is omitted in moving average autoregressive
(ARMA) scheme, while in the autoregressive scheme (AR) both P and E are
omitted. In AR models, fixing kT = 1, one obtains that the unique
weight W1 in linear combination is directly related to the
autocorrelation factor of variable T at time step .
Many authors assert that non-linear approach allows modelling of complex
dynamics in climatic variables. For such a reason the classic BJ model may be
reinterpreted from a neural point of view (Fig. 2 (click here)), the most
important difference is that changes in a non-linear function
realised by the neural network giving the NLAR, NLARMA and NLARMAX models.
Figure 2: Implementation of an ARMAX model thru a NN scheme. Input nodes
are temperature (T), pressure (P) and error propagation estimation
(E) values for different time lags. kT, kP and kE are the number
of past regressors used for each estimation