The results for the energy levels, oscillator strengths, and total and partial photoionization cross sections are described in the following sections.
| Conf. | Term |  |  |  | Conf. | Term | | | | |
 |  | -3.984 | -3.961 | -4.028 |  |  | -2.229 | -2.214 | -2.266 | |
|
|  | -3.665 | -3.640 | -3.734 |  |  | -2.184 | -2.189 | -2.237 | |
|
|  | -3.660 | -3.585 | -3.706 | |  | -2.115 | -2.135 | -2.184 | |
|
|  | -3.613 | -3.563 | -3.674 |  |  | -2.005 | -2.035 | -2.090 | |
|
|  | -3.485 | -3.426 | -3.548 |  | | -1.971 | -2.024 | -2.075 | |
 |  | -2.941 | -2.774 | -2.857 |  |  | -1.967 | -2.035 | -2.065 | |
|
| | -2.795 | -2.685 | -2.767 | |  | -1.972 | -2.006 | -2.058 | |
 | | -2.648 | -2.531 | -2.616 | |  | -1.936 | -1.997 | -2.048 | |
 |  | -2.618 | -2.531 | -2.620 | | | -1.932 | -1.987 | -2.038 | |
 | | -2.613 | -2.516 | -2.605 | | | -1.949 | -1.988 | -2.040 | |
 | | -2.580 | -2.488 | -2.578 | | | -1.910 | -1.970 | -2.026 | |
 | | -2.523 | -2.427 | -2.519 |  | | -1.906 | -1.956 | -2.010 | |
|
|  | -2.275 | -2.256 | -2.303 | | | -1.902 | -1.959 | -2.012 | |
|
|  | -2.267 | -2.250 | -2.296 | | | -1.877 | -1.929 | -1.982 | |
 | | -2.280 | -2.194 | -2.292 |  | | -1.819 | -1.900 | -1.959 | |
 | | -2.270 | -2.198 | -2.293 | | | -1.816 | -1.895 | -1.947 | |
|
| | -2.226 | -2.224 | -2.274 | | | -1.806 | -1.882 | -1.939 |
,
with the
previous OP
results, 
, by Sawey & Berrington (1992), and observed
energies, , from Sugar & Corliss (1985)
The calculations begin with the energies of 746 LS terms
of Fe IV corresponding to
all possible bound states with principal quantum number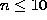 
.
In Table 3 (click here) we compare the computed energies for these terms with those
calculated by SB, and experimental values
from Sugar & Corliss (1985).
The energies obtained in the present work, especially those for the low lying
states, agree typically within 2% with the experimental
values. This level of agreement, for most terms, is better than the
results of SB.
Dipole oscillator strengths (f-values) for 34,635 transitions among the calculated states of Fe IV were obtained in LS coupling. This set includes transitions for which the lower state lies below the first ionization threshold and the upper state lies above. These transitions can be important in opacity calculations because they contribute to the total photo-absorption, but do not appear as resonances in the photoionization cross sections (strictly speaking, the upper bound state does autoionize if departure from LS coupling is considered and fine structure continua are explicitly allowed).
In the absence of experimental f-values it is difficult to
ascertain the overall accuracy of the data. However, a comparison of
length and velocity oscillator strengths provides a systematic
consistency check on the
accuracy of the wavefunctions and, therefore, on the
reliability of the f-values. In Fig. 1 (click here) we plot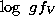 
vs.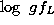 
.
We have included all the symmetries since each
exhibits roughly the same dispersion. The dispersion between length and
velocity values with gf's greater than
unity < 13% for the quartets, and < 22% for the sextets.
This, added to the
good agreement between the calculated energies and those observed
experimentally, suggests that the overall uncertainty for such
transitions should be 20% or less. However, weaker transitions
are likely to have greater uncertainties.
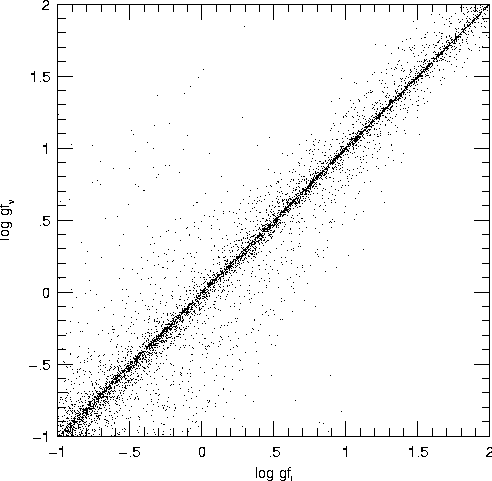
Figure 1: log gfV plotted against log gfL for transitions between
calculated LS terms
Table 4 (click here) presents a comparison of the present gf-values with those of SB and Fawcett (1989) for a small sample of transitions. Fawcett's work is based on a semi-empirical adjustment of Slater parameters in the relativistic Hartree-Fock code by Cowan (1981) to minimize the differences between calculated and observed wavelengths. Very good agreement between the present results and Fawcett's values is observed for most transitions.
| Configuration | Transition | Present | SB | Fawcett |
 |  | 6.11 | 5.92 | 6.11 |
 | 10.2 | 9.83 | 8.49 | |
 | 13.8 | 13.3 | 13.9 | |
 | 3.77 | 3.64 | 2.20 | |
 | 7.02 | 6.67 | 6.57 | |
 | 9.17 | 8.79 | 8.75 | |
 |  | 12.7 | 11.5 | 12.0 |
 | 17.5 | 16.6 | 16.9 | |
 |  | 0.11 | 0.08 | 0.10 |
 |  | 0.11 | 0.08 | 0.10 |
 |  | 1.90 | 2.24 | 1.94 |
Photoionization cross sections were calculated for all 746 bound states of
Fe IV considered here. These cross sections include detailed
autoionization resonances
resulting from the coupling to states dominated by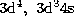 
, and
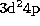configurations in the core ion.
Figure 2 (click here)a shows the
photoionization cross section of the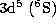 
ground state
of Fe IV. In
the same figure we have plotted the
results of Reilman & Manson (1979)
and those of SB. One interesting feature in the
present cross section is the huge resonance, more than 1 Ry wide and
two orders of magnitude higher than the background, just above
the ionization threshold. Such a feature should have a
large effect on the ionization rate and the opacity of Fe IV; thus a
careful and detailed study of this resonance is worthwhile.
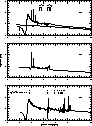
Figure 2: Photoionization cross section (
(Mb)) of the ground
state 
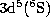of Fe IV as a function of
photon energy (Rydbergs).
a) the cross section obtained with the present
31CC expansion (solid curve); b) the cross section
excluding the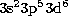 
configuration; c)
the cross section with the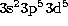 
target terms of Fe V
included explicitly (the Rydberg series
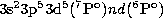for n=3 to 10 is marked).
The dashed curve shows the results of Sawey & Berrington (1992) and the
filled dots, those of Reilman & Manson (1979)
The first thing to investigate is what electron configuration of the Fe IV system is responsible for the resonance, and whether this is possibly a pseudo-resonance that sometimes arise in close coupling calculations owing to inconsistencies between the two summations in Eq. (1). Pseudo-resonances can arise if the first summation involving all channels coupled to the target terms does not explicitly include the parent configurations of some (N+1)-electron correlation configurations included in the second summation. Such configurations then do not have corresponding thresholds for the Rydberg series of resonances in the target expansion (first summation in Eq. (1)). These manifest themselves as large pseudo-resonances, which in a sense represent the entirety of resonance series belonging to the missing thresholds. In order to rule out this possibility, the ground state cross section was calculated several times with different subsets of the (N+1)-electron correlation configurations list given in Table 2 (click here).
It appears that the configuration 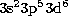gives rise to
the particular resonance. Figure 2 (click here)b shows the cross section obtained when this
configuration is excluded. The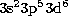
configuration of Fe IV corresponds directly to the
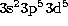correlation configuration in the expansion for
the Fe V core ion. Thus, this resonance appear to be
real. In addition, the term energies for Fe IV
calculated with an accurate CI expansion that includes the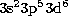
configuration, using the code SUPERSTRUCTURE (Eissner 1991), indicates that
an autoionizing
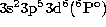state is indeed expected at about 4.58 Ry above the
ground state. That the energy of this state agrees well with the position
of the resonance adds weight to our identification.
As this resonance arises from th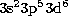e
configuration in Fe IV, one might expect that explicit inclusion in the
calculation of the thresholds
due to the 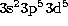parent configuration in the Fe V target would change
the shape
of the resonance and even break it into a series of narrow
Rydberg resonances. The list of term energies for Fe V
in the present target expansion reveals that above these 31 terms
the next higher terms coupled to the ground state of Fe IV
are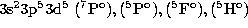 
. Therefore, the ground state cross section was re-calculated
including these states; the result is shown in Fig. 2 (click here)c.
A number of narrow resonances converging on to the new thresholds
are present; however, the large resonance under investigation
remains unchanged.
The more extended calculation also allows for a better identification of the
origin of the resonance, which seems to belong to the
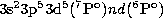Rydberg
series, as indicated in Fig. 2 (click here)c, for n= 3 to 10.
An alternative series could be the
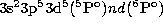; however, the percentage
channel contribution with the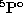 
parent is smaller.
Thus the nature of the large resonance in the ground state cross section
seems to be understood, and its identification as
the autoionizing equivalent electron state 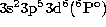explains
in large part the broadness of the feature.
Nevertheless, one should be aware that the position of the
resonance may be uncertain in the absence of experimental data for the
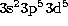thresholds in Fe V. Also,
the position of the resonance in the present calculation relies entirely
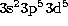on the accuracy of the wavefunctions, which is rather
difficult to assess.
The failure of other authors to obtain resonance structures in the cross
sections
is due to the absence of the relevant electron
correlations in those calculations.This is always the case for the
central field
approximation used by Reilman & Manson (1979).
The close-coupling calculation by SB included only the
16 states of the target ion dominated by the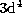 
configuration. This
means that only contributions from the 
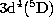ground state of the
Fe V core ion were included in the photoionization cross sections of
states with multiplicity (2S+1)=6. Therefore, all coupling effects for
the cross sections of these states and, in particular, of the
the ground state of Fe IV, were also missing.
In constructing non-LTE spectral models of astrophysical objects it may be important to determine accurately the populations of excited levels of the residual ion following photoionization. This requires not only total photoionization cross section but also partial cross sections into the excited states of product ion. Therefore, we have obtained the partial cross sections for photoionization of the states of Fe IV into at least the lowest few (particularly the metastable) terms of Fe V. These partial photoionization cross sections are also necessary in the calculation of unified electron-ion recombination rate coefficients (Nahar & Pradhan 1995). Fig. 3 (click here) presents these partial cross sections for photoionization of some excited states of Fe IV into the ground state of Fe V.
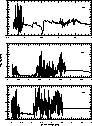
Figure 3: Partial photoionization cross sections of some excited states
(
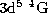, panel a);
(
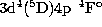, panel b);
(
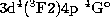, panel c))
of Fe IV into the ground state of Fe V
One interesting feature observed in certain photoionization cross sections
ia the so-called photoexcitation-of-core (PEC) resonances that result
from strong dipole transitions between the ground state and opposite
parity states within the
target ion (Yu & Seaton 1987; see also Bautista & Pradhan 1995, for
Fe I). The PEC features are prominent in the photoionization of excited
bound states along a Rydberg series, as the outer electron is weakly
bound and photo-excitation takes place within the ion core - the
PEC process is thus the inverse of the di-electronic recombination
process with the outer electron as a "spectator" (Nahar
& Pradhan 1995). Such PEC resonances are seen in Fig. 4 (click here) which
displays the photoionization cross sections of Fe IV bound states in the
Rydberg series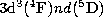 
with n = 5-9.
At the Fe V target thresholds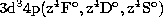 
, the
incident photon energies equal those of
the strong dipole transitions from the ground state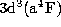 
and
large PEC autoionizing resonances are formed, enhancing the effective cross
section up to several orders of magnitude above the background.
The prominent peaks shown in Fig. 4 (click here) correspond to these dipole
transition energies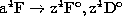 
.
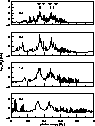
Figure 4: Photoionization of bound states in the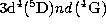 
Rydberg series showing PEC resonances