Numerous diagnostics for various plasma parameters are available in the spectra observed by SUMER. In this section we give examples of electron density and temperature diagnostics, and a line intensity ratio that is suggestive of non-equilibrium effects.
Turning first to electron density measurements, we consider the
intensity ratio
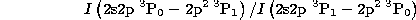
in the Beryllium-like sequence. In N IV these lines fall at 924.283 Å and
921.992 Å, and in O V at 759.441 Å and 761.128 Å respectively.
For Gaussian line pairs with identical FWHM, peak intensity ratios can be taken.
Taking level populations from Keenan et al. (1984) these
ratios are plotted as a function of density in Figs. 6 (click here) and
7 (click here).
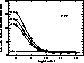
Figure 6: Plot
of the intensity ratio I(924.28)/I(921.99) of N IV as a function
of density, in photon units, for logarithmic electron temperatures
of 4.9, 5.2, and 5.5, indicated by the three solid lines.
The observed ratio, 1.4, is shown by the dotted line, and indicates
densities of just greater than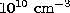 
, depending slightly
on the assumed temperature
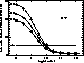
Figure 7: Plot
of the intensity ratio I(759.44)/I(761.13) of O V as a function
of density, in photon units, for logarithmic electron temperatures
of 5.2, 5.5, and 5.8, indicated by the three solid lines.
The observed ratio, 5.6, is shown by the dotted line, and indicates
densities of just less than 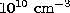, depending slightly on
the assumed temperature
Curves are given
for the temperature at which these ions have their maximum fractional abundance
as given by Arnaud & Rothenflug (1985), and for temperatures a
factor of two above and below these. As can easily be seen, the O V ratio
allows a density of about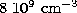 
to be inferred, while
the N IV ratio suggests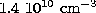 
. Hence both ratios
are consistent with a pressure of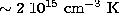 
.
Electron density diagnostics at higher temperature are available in the
spectrum of Ne VI, in the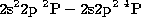 
multiplet with lines around 1000 Å
(see Keenan et al. 1994 for a detailed description).
Temperature diagnostics are available in the ratio
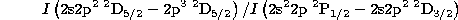
in the Boron-like sequence. Taking electron impact excitation rates from
Stafford et al. (1994) for N III and Zhang et al.
(1994) for O IV, A-coefficients from Nussbaumer & Storey
(1979) for N III and Nussbaumer & Storey (1982) for
O IV, supplemented by values from Dankwort & Trefftz (1978)
for some of the higher lying levels, these ratios are plotted as a function
of temperature for electron densities of 109, 1010, and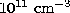 
in Figs. 8 (click here) and 9 (click here).
Figure 8: Plot
of the intensity ratio I(979.92)/I(989.79) of N III as a function
of temperature, in photon units, for electron densities of 109,
1010, and 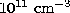, indicated by the three solid lines.
The observed ratio, 0.033, is shown by the dotted line, and indicates
temperatures of about 90000 K, depending slightly on the assumed density.
For comparison, the temperature at which the abundance of the 
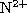ion
is maximized is 80000 K (Arnaud & Rothenflug 1985)
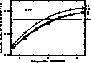
Figure 9: Plot
of the intensity ratio I(779.91)/I(787.71) of O IV as a function
of temperature, in photon units, for electron densities of 109,
1010, and 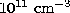, indicated by the three solid lines.
The observed ratio, 0.033, is shown by the dotted line, and indicates
temperatures of about 200000 K, depending slightly on the assumed density.
For comparison, the temperature at which
the abundance of the 
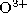ion is maximized is 160000 K (Arnaud
& Rothenflug 1985)
Proton rates between the fine structure levels of the
ground configuration and among the fine structure levels of the
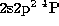term are also included, calculated in a manner similar to
that described for dipole transitions in Laming et al. (1996).
Agreement between these rates and the more sophisticated calculations for
the ground configurations only of Heil et al. (1982) and
Foster et al. (1996) is very good. The temperature inferred
from the N III ratio,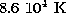 
, (for a density of 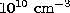) is just slightly above the temperature of 
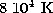where
the ion fraction for 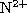should be maximal, according to
Arnaud & Rothenflug (1985). For O IV, the temperature at the
same density is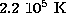 
, rather higher compared to the prediction
of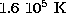 
, also from Arnaud & Rothenflug (1985).
A further temperature diagnostic is possible with the ratio
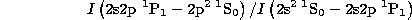
in N IV with lines falling at 955.33 and 765.15 Å respectively. Using
data from Keenan et al. (1984) the intensity ratio as a
function of temperature for densities of 109, 1010, and 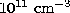is plotted in Fig. 10 (click here).
As in the case with Ne VI, the lines are identified, but difficulties
exist with measuring the 955.33 Å line, partially blended as it is with
two lines from Fe III.
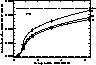
Figure 10: Plot
of the intensity ratio I(955.33)/I(765.15) of N IV as a function
of temperature, in photon units, for electron densities of 109,
1010, and 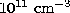, indicated by the three solid lines.
Densities below 109 are indistinguishable from the 109 curve
Temperatures deduced from line intensity ratios higher than those predicted
for the particular ion in collisional ionization equilibrium may indicate
departures from this equilibrium. This would mean that the plasma, instead
of being in a steady state as assumed in the atomic physics statistical
equilibrium calculations, is instead transiently ionizing and recombining.
One ion that is very sensitive to such changes in temperature is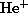 
, due
to the very high (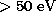
) excitation thresholds for its emission
lines compared to its usual temperature of formation (Laming & Feldman
1992). In Fig. 11 (click here) we plot the intensity ratio of the N III
989.79 line to the He II 992.34 (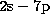
) line, calculated under a few
simple assumptions, to be discussed in more detail below. The two solid
curves give the intensity ratio in the limits that the He II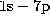 
line is completely optically thick, in which case more radiation comes out
in the Balmer series, or completely optically thin. An abundance ratio
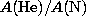of 870 has been assumed (Grevesse & Anders
1989). The curve illustrates the basic result that only for
temperatures considerably in excess of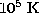 
does the intensity ratio predicted by the calculation start to come
anywhere near the observed value.
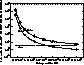
Figure 11: Plot of the intensity ratio I(N III 989.79)/I(He II 992.34)
as a function of temperature, in photon units, for an electron density of
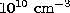. The two solid lines give the intensity ratio under
conditions where the
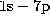Lyman line of 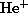is optically thin or thick. The emission
rates for each line are weighted by an abundance ratio He/N of 870, but not
by the ionization fractions.
The observed ratio, 3.76, is shown by the dotted line, and indicates
temperatures substantially greater than 100000 K.
For comparison, the temperatures at which the abundance of the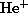
and 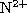ions are maximized are 50000 K and 80000 K
(Arnaud & Rothenflug 1985)
At this stage we should outline the simplifications that have gone into
the calculation. Firstly, the fractional ion abundance for each ion has been
assumed to be 1. Arnaud & Rothenflug (1985) would predict
lower values, but this calculation is not really relevant when considering
departures from ionization equilibrium. Hence the ratio has been formed by
calculating the emission rate in each ion for the range of temperatures, and
by multiplying by the appropriate branching ratio. We have also assumed
that only excitations from the ground state of 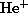are important. Proton
collisions effectively transfer population in the metastable 2s level to the
2p (Zygelman & Dalgarno 1987), and for the optical depths
likely in the He II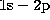 
transition, insufficient population will
be present in the 2p levels to affect the populations of higher lying levels
(Laming & Feldman 1992). We have neglected proton collisions
among the various levels corresponding to n=7, and have calculated the
branching ratio for the Balmer transition in the cases of the optically
thick and thin Lyman transition from formulae for the dipole
A-coefficients given in Bethe & Salpeter (1957). It is
difficult to obtain accurate electron impact excitation rates for such
highly excited levels as n=7. We have taken an approximate collision
strength by scaling the collision strengths for 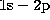and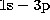 
excitation of Aggarwal et al. (1992) by the ratios of the
absorption oscillator strengths divided by the excitation threshold to get a
value of 0.006. While such a procedure is accurate for asymptotically high
energies, at lower energies (but still above the ionization threshold) it
has been shown (Bray et al. 1993) that continuum wavefunctions
must be included in close coupling expansions to get the excitation
collision strengths correct. Such calculations are available for excitations
between the n=1, 2, 3 levels (Aggarwal et al. 1992) where the
effect of the continuum in reducing the excitation collision strengths may
easily be seen. Thus it appears that our estimate of the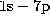
collision strength may well be an overestimate. For these reasons we have
not performed a complete statistical equilibrium calculation
for the He II ion, but just given an estimate of the emission rate. We
emphasise that the processes we have neglected (excluding cascades) will
all act to reduce our predicted He II intensity, making the problem of
anomalously high He II line intensities worse.
The fact that in the absence of diffusion effects (see e.g., Fontenla et al. 1993; Hansteen et al. 1994) which we consider to be unlikely, the He II emission can only be understood quantitatively by increasing the temperature at which its emission is assumed to occur implies that the plasma must be transiently ionizing, and that the electron temperature increases on a timescale fast compared to the ionization time, making the plasma underionized. Such a notion is a radical departure from traditional models of the solar transition region (e.g., Vernazza et al. 1981), but is becoming increasingly favoured in the light of recent data.