Under the ![]() hypothesis, the noise s(t) is assumed
to be Gaussian.
hypothesis, the noise s(t) is assumed
to be Gaussian. ![]() and
and ![]() are characterized by the
total power
are characterized by the
total power ![]() and the normalized autocorrelation function
and the normalized autocorrelation function
![]() of the noise s(t).
of the noise s(t).
From a practical point of view, ![]() depends mainly on the receiver
(e.g. the successive filter shapes). Other contributions to the final spectral shape can be
considered either locally white (e.g. the ground noise) or negligible (e.g. the cosmic source).
Moreover,
depends mainly on the receiver
(e.g. the successive filter shapes). Other contributions to the final spectral shape can be
considered either locally white (e.g. the ground noise) or negligible (e.g. the cosmic source).
Moreover, ![]() being stationary over large durations (>1 hour),
it will be estimated once at the beginning of the observation by using a noise
generator as a virtual non-contaminated source (see Sect. 5 (click here)).
being stationary over large durations (>1 hour),
it will be estimated once at the beginning of the observation by using a noise
generator as a virtual non-contaminated source (see Sect. 5 (click here)).
With regard to ![]() , due to antenna or earth rotation, stationarity can not
be guaranteed beyond a few minutes. It is therefore necessary to take into account
the current
, due to antenna or earth rotation, stationarity can not
be guaranteed beyond a few minutes. It is therefore necessary to take into account
the current ![]() value when computing
value when computing ![]() .
.
Because of the quantization process, the dependence of ![]() and
and
![]() on
on ![]() is not simple. Moreover, the number of operations
required to estimate the test function
is not simple. Moreover, the number of operations
required to estimate the test function ![]() is proportional
to Q2. This can restrain the real time capabilities for large Q. To
circumvent these drawbacks, it is necessary, firstly, to take into account the
dependence on
is proportional
to Q2. This can restrain the real time capabilities for large Q. To
circumvent these drawbacks, it is necessary, firstly, to take into account the
dependence on ![]() in an easy way and, secondly, to reduce the
impact of the
in an easy way and, secondly, to reduce the
impact of the ![]() matrix
matrix ![]() on the computational time.
on the computational time.
Knowing the normalized autocorrelation function ![]() for each
involved time lag, the reference vector
for each
involved time lag, the reference vector ![]() depends only on
depends only on ![]() :
:
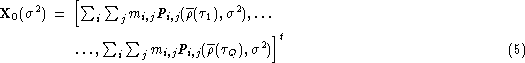
where ![]() is the joint probability that
two Gaussian variables
with zero mean, equal variance
is the joint probability that
two Gaussian variables
with zero mean, equal variance ![]() , and with normalized correlation
coefficient
, and with normalized correlation
coefficient ![]() belong to the
belong to the ![]() area.
area.
So, the ![]() variation with
variation with ![]() will be given by Q
(one for each component of the vector), second order polynomial approximations
of Eq. (5 (click here)). These approximations must be valid within the expected
fluctuation domain of
will be given by Q
(one for each component of the vector), second order polynomial approximations
of Eq. (5 (click here)). These approximations must be valid within the expected
fluctuation domain of ![]() under the
under the ![]() hypothesis.
hypothesis.
A general formula for ![]() is complicated by the correlation between
the samples sn. One solution is to keep the sample uncorrelated by forcing
the Nyquist property (Nyquist 1928) on the noise under the
is complicated by the correlation between
the samples sn. One solution is to keep the sample uncorrelated by forcing
the Nyquist property (Nyquist 1928) on the noise under the ![]() hypothesis. Generally, this can be achieved by slightly modifying the receiver
spectral shape, so that the periodic zeros in the correlation function occur at
a known periodicity. Independence between samples can be guaranteed by sampling
the noise with this known rate. This method leads to an exact and computable
hypothesis. Generally, this can be achieved by slightly modifying the receiver
spectral shape, so that the periodic zeros in the correlation function occur at
a known periodicity. Independence between samples can be guaranteed by sampling
the noise with this known rate. This method leads to an exact and computable
![]() formula but requires some modifications of the receiver.
formula but requires some modifications of the receiver.
An alternative solution would be to neglect the dependence between samples
and to simply consider the noise under the ![]() hypothesis
as a white noise despite its band limitation. This simplification induces to a
change in the weighting factors of the errors between the
hypothesis
as a white noise despite its band limitation. This simplification induces to a
change in the weighting factors of the errors between the ![]() and
and
![]() components and makes the criterion less than optimal.
components and makes the criterion less than optimal.
Under either of these previous hypotheses, the matrix ![]() becomes diagonal:
becomes diagonal:
where ![]() is the unit matrix.
is the unit matrix.
Therefore, no matrix inversion is needed and the number of operations necessary
to compute the test function ![]() becomes proportional to
Q. Furthermore, its variation with
becomes proportional to
Q. Furthermore, its variation with ![]() can be computed as a second
order polynomial approximation.
can be computed as a second
order polynomial approximation. ![]() becomes a classical
quadratic mean error test.
becomes a classical
quadratic mean error test.
| g(x1,x2) | |||||||||||||||||||||||||||||||||||||||
| Quantization levels li ( | (0 0.436 1.017 1.67) | ||||||||||||||||||||||||||||||||||||||
| Product table mi,j |
| ||||||||||||||||||||||||||||||||||||||