Adaptive optics works in many cases in the partial correction regime, i.e. with a Strehl ratio smaller than 0.8. Here, I emphasize the characteristics of such partially corrected psfs. The temporal and geometrical properties are therefore described.
In the partial correction regime, seeing evolution during the night induces some variations in the mean correction (Rigaut et al. 1991). It is shown by following up the Strehl ratio which is an excellent tracer of the correction. We now try to look at what is going on during a typical integration time of a few minutes. Table 2 (click here) gives the mean and the standard deviation of the scalars for 1s psfs recorded continuously for 5 minutes. One can see that for good Sr, the fwhm is stable but not the r50. By contrast, for lower Sr, the r50 gets more stable and the fwhm fluctuates a lot.
As seen in Fig. 1 (click here), the Sr of continuous short exposure (2s) frames appears to be highly variable in time. First, these variations may be explained from the statistics of the wavefront error reconstruction. Literature lacks explicit calculation of the variance of the AO correction (Strehl ratio) for a given integration time and wavefront statistics (see however Johnston et al. 1996 for a recent example). But this is probably not responsible for such high variations even if some temporary close loop failures due to the finite bandwidth of the system may account for some. Seeing evolution is probably responsible for structures like slopes and breaks as seeing is known to vary in such a way. Any conclusion should be taken cautiously but the psfs stability may be more limited by the seeing statistics than by the AO system itself (Tessier 95). Actually, to decide this issue, it will be interesting to correlate Sr measurements to the r0 and t0 measurements from a seeing monitor looking at the same viewing direction.
Figure 1: Strehl ratio as a function of time from continuous
2 seconds exposure
frames. Sr is normalized to its mean value to highlight relative variations.
Sr is shifted for H data for readability. Data at H and K are not
simultaneous but were taken a few minutes apart. One uses the same scale
for convenience. Come-on + data
From Fig. 2 (click here), the fwhms of short exposure psfs are quite well stabilized in K when Sr is higher than 20%; fwhms being always smaller than 0.18 arcsec (except for a few seconds). But in H, the Sr has dropped about 10% and some large variations of the fwhm between 0.13 arcsec and 0.25 arcsec are observed. This will be explained by the close relationship between these two parameters (further in this section).
Figure 2: Same as Fig. 1 (click here) but fwhms
is plotted instead. Come-on + data
Sets of Psfs with equivalent integration time ranging from
2 s to 30 s have been computed from a cube of 2 s frames
taken continuously for 5 minutes in the K band with
a mean Sr of 0.25 and in the H band with a mean Sr of 0.08.
The statistic p(t,r) is defined to be the pixel value
at a given radial distance r to the central peak for a psf
integrated over a time t. The minimum integration time
was long enough to get no temporal
correlations between frames. The source was selected bright to
dominate the readout noise (the limiting
noise) effects even in the wings of the signal.
Readout noise contribution has been removed from the next results.
When this contribution is significant,
the removal does not allow a satisfactory accuracy. Consequently,
graphs are cut at 2 arcsec.
Figure 3 (click here) shows the behavior of the standard deviation
normalized to the mean computed from the set of psfs with t=2 s
during the 5 minutes window in
function of the radial distance to the psf peak. For the purpose
of a sequential calibration of the point spread function (see Sect.
4 (click here)), this term is presumably inversely proportional to the
signal to noise ratio. Thus, the signal to noise
appears to be quite constant but a bit smaller
to the outer halo and near the center.
Figure 3: Standard deviation normalized to the mean value
per pixel as a function of its radial distance to the central psf peak
from a set of continuous psf frames with t=2 s recorded for 5 minutes.
Plot is shown for two Strehl ratios: 25% and 8% at KH respectively.
The pixel size is 50 mas. Come-on + data
At a given radial distance from the peak, the temporal behavior of the standard deviation for 1 < t < 20 s computed over the 5 minutes window is well fitted by a power law function as in t-n. Figure 4 (click here) shows the n parameter as a function of the radial distance for both Sr. The standard behavior in square root of time corresponds to n=0.5 is not found and the signals do not average well with the time, especially near the center. The psf statistics shows atypical behavior which is the reflect of the seeing statistics through the AO system. While the standard deviation normalized to the total energy is as expected lower when the Strehl ratio gets higher, the standard deviation normalized to the mean shown in Fig. 3 increases significantly. Similarly, the temporal behavior for the psf appears to be different with the Strehl ratio as shown by the Fig. 4. This would suggest that the seeing statistics induce amplified effects with Sr increasing, in the sense that the signal to noise ratio as defined earlier in the residual halo declines. We noted a similar fact for the r50 earlier. These results can be used to assess the consequences for the sequential calibration procedure (see Sect. 4 (click here)).
Figure 4: The standard deviation per pixel (see previous figure)
follows a power law as in t-n where t is the integration time
of the psf.
n is given as a function of the radial distance to the central psf peak.
Plot is once again shown for two Strehl ratios: 25% and 8% at KH respectively.
The pixel size is 50 mas. Come-on + data
The morphology of the on-axis point spread function is now seen for different levels of correction. Figure 5 (click here) shows that how the psf halo gets smoother as the integration time increases. The speckle pattern vanishes but some residual features like the secondary mirror spider spikes or the waffle diffraction patterns and also non-identified spatial correlations could be seen on the long-exposure psf. The last ones are not static and could vary. The waffle effect is due to the to the piezo-actuated deformable mirror.
Figure 5: Psfs integrated over 2, 8, 32
and 120 seconds. The residual
speckle pattern is smoothed to a seeing halo. Some known pattern
are seen like the waffle diffraction pattern.
Sr is about 0.25 in these K images. Come-on + data
Long-exposure psfs from COP do not in general show any major deviation from circular symmetry. In average, the relative deviation is below 20%. However, at a closer range, psfs show some intensity enhancements especially onto the first Airy ring area. These patterns are not fixed and could vary along the night and on short time scale. They do not average out even for long exposure time. Some SOR Gen II psfs have shown a significantly elongated psf. Possible causes are some uncorrected static aberration in the imaging channel, temporal anisoplanatism but in this case, a suspected jitter in the telescope control is probably responsible.
Figures 6 (click here) and 7 (click here) plot long-exposure psf profiles for different Strehl ratios. These profiles have been obtained by azimuthally averaging the images. Here the profiles are shown normalized to one at the peak. The profiles normalized with the total energy can be obtained by multiplying these previous profiles by their respective Strehl ratio which corresponds to a basic shift for Fig. 7 (click here) in logarithmic scale. In linear scale, the profile of the best image available in K with a Strehl ratio of 0.40 compares well with the theoretical diffraction-limited psf. In logarithmic scale, these profiles drops down to 10-3 pretty close to the source for good corrections. Away, the brightness profiles decrease in parallel lines with a slope of -3 which is consistent with the theoretical profiles of diffraction-limited psfs computed for instruments with obstruction (see Schroeder & Golimowski 1996). But, the brightness level is higher (1 or 2 orders of magnitude) certainly because of the small-scale imperfection of the optics surfaces.
Figure 6: Profiles of the psfs for different Strehl ratios from
COP and SOR Gen II data
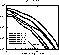
Figure 7: Same as in Fig. 6 (click here) but in logarithmic scale
Psf scalars have been defined in Sect. 1 (click here).
Full width half maximum and Strehl ratios for various psfs have been
located in a diagram in Fig. 8 (click here).
Psfs are from different observing runs, bands and
turbulence conditions. The scale
has been normalized to 
.
Both parameters appear to be closely related
(Tessier et al. 1994; Tessier 1995)
as the points clearly gather along
a single curve with some scattering. Parameters like the wavelength,
the time or the integration time have no measurable effect on the diagram
shape.
This curve could be also interpreted as an AO response curve.
More specifically, it is the psf response of the Come-on+
experiment. Incidentally, the curve is pretty well fitted by the
basic function defined as:
As shown by this curve, a fast widening of the psf is observed as soon as the Strehl ratio drops below a value of 10%. This value should be kept in mind as a transition. Images with a Strehl lower than this value will not conserve a diffraction core.
Some psfs from Gen II are overplotted in Fig. 8 (click here) and
fit again the curve. Most of these psfs were recorded within half an hour
where average seeing conditions correspond to 
and
Hz.
The AO bandwidth system was tuned at three different bandwidths
to change the correction degree and thus to draw the curve.
However, others or future AO systems may give different
responses; due to the limited bandwidth of the two presented systems,
the first modes of the turbulence are not totally compensated
(see Conan et al. 1995 e.g.); some systems with a higher bandwidth
may compensate better the first modes of the turbulence
in any conditions and produce low Strehl ratio
psf with a sharp core.
Figure 8: Position of the psf in a 
diagram
for the Adaptive Optics system COP in JHK and
for SOR Gen II in the I band. Fwhm is rescaled by to show
the relationship between Sr and fwhm. Some theoretical
predictions are also plotted. See text
Figure 9 (click here) and 10 (click here) show
the psf location in 50% energy radius versus fwhm and
Sr respectively diagrams. The plots show a scattering larger than
in Fig. 8 (click here) and appear to be less constrained by the AO system and
may vary with the conditions: seeing, wavelength. For example,
five SOR psfs corresponding to but very
fast turbulence (Greenwood frequency estimated at 125 Hz) are clearly
located in a different part of the diagram compared to the other SOR psfs.
As a first approximation, r50 is linearly related to Sr for Sr
between 0.05 and 0.30. As the Sr goes below 5%, r50 increases steeply:
some measurements like (10.4, 0.008), (10.7, 0.007) are out the frame.
By contrast with Fig. 8 (click here), the two
AO systems show significantly different responses (to SOR's advantage).
For reference, we give the r50 to fwhm ratio for the
theoretical diffraction-limited psf (full correction). This ratio which
depends on the obstruction U of the telescope
is 
for the 1.5 m SOR telescope (U=0.07),
and increases to 
for the 3.6 m ESO telescope (U=0.44); for a pure Gaussian r50
it is equal to 0.5.
Figure 9: Same as in Fig. 8 (click here) but
the psfs are located in a
diagram
Figure 10: Same as in Fig. 8 (click here) but the psfs
are located in a
diagram
To recapitulate, the experimental data shown here correspond to bright sources and the following relevant parameters: D/d = 7 and 16 for COP and Gen II respectively, d/r0 between 0.5 and 3, mostly 1 and 2 in fact (where d is the subaperture width, see Sect. 2 (click here)). Actually, the high and low Strehl ratios often correspond to d/r0 = 1 and 2 respectively, but fast turbulence has also some effects through the AO bandwidth to Greenwood frequency ratio. Consequently, B. Ellerbroek has kindly generated a set of theoretical optical transfer functions (OTF) with a WFS geometry of D/d = 8 for the cases d/r0 = 1 and 2 to compare with the COP experimental data. These predictions are based on analytical and covariance calculations in Ellerbroek (1994) which incorporate all the details of the AO system including the modal optimization (Ellerbroek et al. 1994; Gendron & Léna 1994). Different corrections have been obtained by varying the rms WFS noise (from 0 to about 0.5 waves per subaperture) or the servo lag (translation from 0 to about one subaperture per time constant of the servo in a single turbulent layer model). Figures 8 (click here) and 9 (click here) compare the experimental data to the theoretical predictions extracted from the OTFs. The predictions are consistent and satisfactory confirming the close relationship for Sr versus fwhm while r50 depends a lot on d/r0. It is possible that the experimental results are less scattered than the theoretical estimates because the high Strehls were obtained for low values of d/r0, and conversely as we have above pointed out.
We now define the scalar fcut as the spatial frequency cutoff at 40dB of the
power spectrum. fcut is a good indication of the fall-off in the power
spectrum
(see Sect. 7 (click here)). However, the spatial
frequencies higher than fcut
may have not vanished. For example, applying this metric
to the pure diffraction-limited psf, fcut is equal to 96%
(in 
units). Figure 11 (click here) shows
fcut as a function of the Strehl ratio.
The curve shape compares well with Fig. 8 (click here).
Both systems give the same response as in Fig. 8 (click here).
In fact, fcut is pretty well linearly related to the fwhm as shown
by the
plot in Fig. 12 (click here) (as expected).
Figure 11: Same as in Fig. 8 (click here)
but the psfs are located
in a 
diagram. See text
Figure 12: Same as in Fig. 8 (click here) but
the psfs are located
in a fwhm - fcut diagram. See text
Psf scalars like Sr, fwhm and r50 are in fact a crude description of the psf. Psfs are not perfectly smooth and circular symmetric. Psfs lie in a hyperspace so that it is not realistic to model a psf with a few parameters or with a synthetic function. For a same Sr, profiles and patterns could vary significantly on short time scale and one reminds that from hour to hour, the instrumental transfer function could vary as well; so that the idea to represent this hyperspace by a collection of psfs done once for all science observations is not relevant.
From these results, several conclusions can be drawn:
diagram
so that Sr and fwhm are connected in practice independently of the seeing
and the wavelength. These diagrams could be used to direcly infer
expected fwhm, r50 from a Sr estimation
for a given AO system and turbulence conditions. We note
that for both systems studied here the fwhm degrades dramatically for a Sr
smaller than 10%. However, the previous diagrams might be AO
system dependent.
(Sr)/Sr 
