It has been known for more than three decades that axes of isophotal contours in many elliptical galaxies rotate (e.g. Liller 1960; Bertola & Galletta 1979; Nieto et al. 1992). Such twists can be explained either by intrinsic misalignement of isophotal surfaces (which are ellipsoidal in the first approximation) or by projection effects: in the latter case, the aligned ellipsoids must be triaxial and their eccentricity must vary with radius at the same time. Models (e.g. Madejsky & Möllenhoff 1990) show that even a moderate triaxiality can produce a considerable twist if one looks at an elliptical galaxy under oblique view.
Figure 1: Ellipticities (1-b/a), position angles (PA) and
contour plots for a single 2D bar: a) Face-on view - full lines in
plots of radial profiles (dotted lines indicate the same quantities
measured after the bar is first analytically projected and then
numerically deprojected back; see the text),
b) Projection with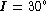 
and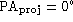 
,
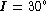c) Projection with and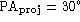 
It is natural to expect the isophote twist due to projection effects also in the case of galactic bars since they are obviously triaxial and their eccentricity shows a radial variation (as seen in galaxies viewed face-on). In looking for a correlation between central activity and isophote rotation, one should separate the intrinsic twists, related to dynamics, from mere projection twists.
The solution of such a task is outside the scope of this paper. Nevertheless we would like to initiate the discussion on that topic by several simple illustrative examples of projection effects on artificially constructed single and double bars.
Figure 1 (click here)a shows
the ellipticity and PA profiles of a face-on viewed 2D bar,
whose isodensity
contours are perfect ellipses with axial ratio a/b varying radially
from 1 to 3.
After projecting (with only moderate inclination, 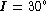) about the
line with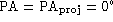 
(i.e. coinciding with the bar minor axis),
the 
along the bar becomes two-fold, with two plateaus separated by a
sharp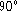 
-transition at which the ellipticity falls locally
to zero (Fig. 1 (click here)b). With the same I but 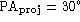, one obtains
a gradual twist of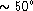 
(Fig. 1 (click here)c).
A 2D double barred system with
the inner component perpendicular to the outer one
is presented in Fig. 2 (click here)a: the large-scale bar is the same as in
the above case;
the small one is 7 times shorter and its axial ratio a/b varies
linearly from 1 to 2.
The projection with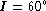 
and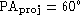 
is
shown in Fig. 2 (click here)b: the local ellipticity maximum corresponding
to the secondary bar nearly disappears; the PA varies along both
primary and secondary bars.
Finally, a system of two parallel bars (with the same parameters as
above) is shown in Fig. 3 (click here)a. The projection by 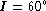about
the minor axis of both bars (i.e. 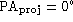) results in an
illusion of two perpendicular bars (Fig. 3 (click here)b).
The above examples clearly demonstrate that the projection
is a crucial factor for classifying twists and double bars.
To disentangle projection effects from intrinsic distortions, one
can try to deproject the observed images, making use of two advantages
spiral galaxies have with respect to ellipticals: a) they
are fairly two-dimensional except the bulge region and b) the inclination
I and position angle can be deduced from the shape of the outer disk
under the assumption that it is intrinsically circular. A two-dimensional
body with known I and can be deprojected without ambiguity:
if conditions a) and b) were strictly met, the problem would be solved.
Nevertheless many complications exist: the bulge is clearly three-dimensional;
the primary bar may also be significantly thickened close to the center
due to the scattering on vertical resonances (e.g. Combes et al. 1990);
the secondary bar, when it exists, is confined to that bulge-bar
3D region; the outer disk has not necessarily the intrinsic circular
shape which can result in substantial errors in determining I and .
Figure 2:
Ellipticities (1-b/a), position angles (PA) and contour plots for a
a 2D double bar - bars perpendicular:
a) Face-on view,
b) Projection with 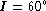and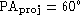
Figure 3:
Ellipticities (1-b/a), position angles (PA) and contour plots for a
a 2D double bar - bars parallel: a) Face-on view,
b) Projection with 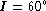and ,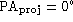
In this paper, we have deprojected, under the assumption of
two-dimensionality, galaxies with inclination
lower than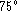 
, and we present, in the appendix, the deprojected
radial profiles together with the projected ones.
Since outer disks are usually located outside our images, we have used
disk inclination and position angles quoted in the Lyon-Meudon
Extragalactic Database (LEDA, Paturel et al. 1989).
The deprojection can be done in two ways: either the image
is first deprojected and then a new ellipse fitting is carried out or
the ellipses fitted to the projected image are deprojected analytically.
The two approaches are not completely equivalent because of discreteness
of the detector array and because the isophotes are not perfect ellipses.
Our experiments have shown that the first method is less reliable:
after deprojecting the image, one has to interpolate to get intensity
at pixel positions which causes numerical errors resulting
in spurious variations of ellipticity and position angle in the
subsequent ellipse fitting.
We show this effect by dotted curves in Fig. 1 (click here)a: they correspond to
the bar which is first projected with 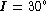and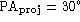
(Fig. 1 (click here)c) and then deprojected back to the face-on position. Both
ellipticity and position angle profiles significantly differ
from the correct ones (full lines) inside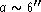 
, possibly giving
illusion of a small secondary bar. This numerical error is expected to
occur in regions with high density contrasts, e.g. close to the center
or at the edges of bars. Therefore we have preferred the second approach.
Whether the deprojected profiles are meaningful or not,
depends on how closely individual galaxies fulfil the conditions a) and b)
given above.
Clearly, in regions with non-negligible thickness, the error
resulting from the deprojection will grow with the galaxy inclination.
As can be seen from the profiles of observed galaxies, the
deprojection does not look reasonable in the bulge region if I
exceeds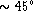 
.
Additional error is introduced by uncertainties in I and 
.
Being aware of big uncertainties in the deprojection procedure,
we do not rely on it to draw firm conclusions about the nature of a twist but
use it only as a secondary help:
if a double bar (or gradual twist) seen on the projected image
remains after deprojection, we consider the probability of its
existence to be strengthened; if it disappears, while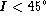 
,
we take it to be a projection effect; on the other hand
if a double bar structure appears only after deprojection,
we do not classify it to be a double bar.