The mass range covered is from 1 to 
for the three chemical
compositions (X, Z) =(0.55, 0.03), (0.65, 0.03) and (0.75, 0.03). I
denote these
grids hereafter as X55, X65 and X75 respectively. Note that for X75, the
abundance of helium is 0.22. This value is a little bit smaller than that
used as primordial abundance of helium (about 0.24). However, this grid is
useful to permit interpolations among stellar properties and isochrones as
explained in the Introduction of the paper Claret & Giménez
1995. The value of Y for the models X65 is obtained by the relation
, with
(the primordial He
abundance) and 
taken equal to 0.24 and 2.7 respectively;
two other values of Y were considered to take into account the
uncertainties in 
and in the derivative . In
Figs. 1 (click here)-6 (click here) I show the HR and log 
diagrams. Figures 4 (click here), 5 (click here) and 6 (click here) are especially
useful to be compared with binary star data given that the masses and radii
in this kind of stars are generally the best determined parameters.
From the comparison among these figures one can note the influence of the
mean molecular weight on the position of the tracks. Let us use simple
homology relations, for example ideal gas and constant opacity, to
interpretate such diagrams. Under such conditions, the radius of a model is
proportional to 
where 
is the mean
molecular weight, 
is the exponent of the density and 
is the
exponent of the temperature in the nuclear energy generation rate. For the
pp chain 
, while 
. For a fixed mass, it is
easy to see that the models X55 - large mean molecular weight - have larger
radii and smaller 
than the corresponding X75 grid. The aspect of
Fig. 7 (click here) can be interpretated using the following argument: let be
fXM the fraction of the stellar mass for which hydrogen is converted
into helium during the lifetime of the star, being f smaller than 1,
X is the initial hydrogen content per mass and M the total mass. The
corresponding lifetime in the main-sequence will be given by the ratio of
the total energy radiated to the average luminosity. In this way, 
fXM/L. A more direct comparison concerning the influence of
the molecular weight on the tracks can be seen in Fig. 7 (click here) where the
lifetimes of the hydrogen burning is shown for the three grids as a function
of the logarithm of the stellar masses. An increase of 0.10 in the initial
hydrogen content implies that the corresponding lifetimes are increased by
about 1.7 times. On the other hand, Fig. 8 (click here) shows the effects of
changing the chemical composition on the effective temperatures for the
models at TAMS, also as a function of the logarithm of the stellar masses.
Note that a variation of 0.10 in the initial helium abundance yields a
difference about 0.08 in 
.
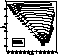
Figure 1: HR diagram for the grid X55. Numbers attached denote 
Figure 2: HR diagram for the grid X65. Same remarks a
Fig. 1 (click here)
Figure 3: HR diagram for the grid X75. Same remarks as
Fig. 1 (click here)
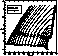
Figure 4: 
diagram for the grid X55.
Same remarks as Fig. 1 (click here)
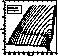
Figure 5: diagram for the grid X65.
Same remarks as Fig. 1 (click here)
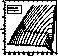
Figure 6: diagram for the grid X75.
Same remarks as Fig. 1 (click here)
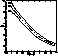
Figure 7: The lifetimes for the hydrogen-burning phase for the three grids.
The grid X55 is represented by a thick continuous line, X65 by a dashed one, and the continuous thin line denotes the grid X75
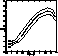
Figure 8: The effective temperatures at the TAMS for the three grids.
Same line types as in Fig. 7 (click here)
Concerning tidal evolution, there are three mechanisms which are being used to study the circularization and synchronization of orbits in CBS. The first two mechanisms, which are based on the classical tidal theory, depend on the characteristics of the stellar core and envelope. On the other hand, Tassoul claimed that the distortions present in CBS cause hydrodynamical currents which tend to circularize their orbits. However, there is a strong discussion on the validity of the hydrodynamical mechanism (Rieutord 1992; Tassoul & Tassoul 1996). I do not discuss here this controversy. The interested readers can consult the original papers quoted above. For a comparison of predictions of the hydrodynamical and tidal-torque mechanisms with observations see Claret et al. (1995) and Claret & Cunha (1996).
I shall concentrate our attention on the first two mechanisms. A star
which belongs to
a binary system is under the action of the disturbing potential due to its
mate.
This star reacts to the external potential through equilibrium and
dynamical tides.
The characteristic time scales for synchronization and circularization in
the case of
turburlent dissipation and radiative damping are given respectively by (see for example
Zahn 1975 and 1989)
where the times scales are in years, the orbital period P in days and the
mass, radius and luminosity are
in solar units. The subscripts circ and sync refer to circularization and
synchronization while turb and rad refer to turburlent dissipation and
radiative damping respectively. The rotational angular frequency is
represented by 
while e is the eccentricity of the orbit, q the
mass ratio, 
the radius of gyration and 
is the orbital
angular frequency. The meaning of E2 and 
will be explained
in the next paragraphs.
The few papers that treat the oscillations driven by the tides do not consider the dissipation in
the mentioned process (e.g. Cowling 1941). In more recent years
Zahn (1975) studied the
effects of the radiative damping in the dynamical tide. This mechanism,
radiative
damping, is the responsible for the synchronization and circularization of
the
orbits when the stars in a given system present convective cores and
radiative envelopes.
The gravity waves, due to the external potential, are damped in the
external layers.
This damping occurs because the radiative cooling time is of the order of
the tidal
period and in this way part of the angular momentum of rotation is
transfered to the
orbital motion. In order to characterize the time scales I use 
.
Such a
parameter can be evaluated using the following equations:
where 
is the gamma function, x is the normalised radius of the
configuration, the symbol f denotes the border of the convective
core, s
indicates surface values, the prime denotes the
derivative with respect to x, R is the
radius, M the mass, g the gravity and B is given by
where -gB is the square of the
Brunt-Väisälä frequency.
The coefficient 
is given by
X is the solution of the differential equation
and Y(1) is the solution of the Clairault equation. The differential equations
were solved for each configuration using a fourth order Runge-Kutta method.
In this Paper I shall restrict the calculations to n = 2 since for larger
n the contribution to the dynamic tide is very small.
Such calculations deserve special attention. Let us rewrite -gB as
where 
is the usual 
ratio, G is the constant of
gravitation, r the radial distance, Mr the mass at the distance r,
P the total pressure, 
,
is the adiabatic gradient and
. As a massive star
evolves the convective core recedes. The zone between the initial and the
present convective core present a large chemical compositon gradient. In
such zone the spatial gradient of chemical composition increases more and
more and becomes wider. This feacture is well known when one analyses a
diagram of propagation. As shown before, the tidal constant depends on the
derivative of the Brunt-Väisäla frequency in the border of the
convective core and the consequent numerical oscillations are clear in
Fig. 9 (click here).
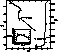
Figure 9: Schematic evolution of E2 (thick line) and
(thin line)
for a 
model with X=0.75 and Z=0.03. The apsidal motion
constant is
denoted by a dashed line.
The attached labels are useful to identify the corresponding evolutionary
phases since that
in the lower left corner I represent the corresponding HR diagram
For stars with envelopes in convective equilibrium another mechanism was
identified: the turbulent dissipation. This process is characterized by
the
parameter though in the last years the apsidal motion
constant
k2 was
used as an approximation. In fact, Fig. 3 (click here) by Claret & Cunha
(1997) shows that it is an acceptable
approximation. A new approach for was obtained by Zahn
1989 using
the mixing-length theory. He obtained
where 
denotes the bottom of the surface convective zone,
is
the mixing-length parameter and E describes a polytropic envelope.
I have evaluated it through the equation
where 
is the mass of the convective envelope. The
approximation
described above is valid when the convective turnover time is smaller than
the
tidal period.
In Fig. 9 (click here) we can see the behaviour of the tidal torque constant and
tidal coefficient for
a . Thick continuous line represents the evolution of E2,
thin continuous
line the evolution of and dashed line denotes the evolution of
k2. The tidal
torque constant decreases quickly as the model evolves. From homogeneous
model to the
hydrogen exhaustion it decays about 4 magnitudes. The contribution of the
equilibrium tide is very small in the main-sequence, as expected. In this
specific
case we have computed this contribution only for models with effective
temperatures
below 8000 K. This contribution increases with the depth of the convective
outer layers.
A rapid
analysis of Fig. 9 (click here) during the phases d-f shows that indeed the
apsidal motion constant
k2 is a good approximation to .
In the next papers of this series we will analyse the influence of the
chemical compositions
and core overshooting on the and E2.
The present models are available in electronic form at the CDS or directly
from the author.
Also, I can provide to interested readers specific calculations or details
which were not
given here.
Acknowledgements
Drs. M.A. López Valverde and G. Meynet are gratefull acknowledged by their useful suggestions. The Spanish DGYCIT (PB93-0134) is gratefully acknowledged for support during the development of this work.