The WENSS project initially concentrated on a relatively small area of sky roughly centered on the North Ecliptic Pole. This region was chosen to coincide with the NEP-VLA survey at 1.5 GHz (Kollgaard et al.\ 1995), the deep 7C North Ecliptic Cap survey (Lacy et al. 1995; Visser et al. 1995), and the deepest part of the ROSAT All Sky survey (Böhringer et al. 1991; Bower et al. 1996) and IRAS survey (Hacking & Houck 1987).
Our original intention was to base our complete analysis of errors and reliability on the mini-survey region. However, data from various other parts of the survey have been included in this analysis. Nevertheless the mini-survey constitutes the most thoroughly analyzed part of WENSS to date. Furthermore, data from the mini-survey has already been used extensively for various follow-up projects, including a search for gravitational lenses (CLASS, Myers et al. 1995; Snellen et al. 1995), and investigations of samples of faint Gigaherz peaked spectrum sources and faint ultra steep spectrum sources.
Frames were constructed from the five mosaics listed in Table
3 (click here). The mosaics are labeled by the declination and
approximate right-ascension of their center. Four of mosaics were
observed at the start of the WENSS project in the spring of 1991. Mosaic
was later included in the mini-survey to improve the overlap
with the 7C survey (Visser et al. 1995). Figure 2 (click here) shows
the layout of these mosaics within the the survey.
A list of the 24 high resolution 92 cm frames included in the mini-survey is presented in Table 4 (click here). The frames are labeled by the declination and approximate right-ascension of their center. Figure 4 (click here) shows the layout of these fields.
Figure 4: The layout of the frames included in the mini-survey. The dots
mark the individual sources assembled in the source list
The theoretical noise level for WENSS is approximately 2 mJy
beam
. Sidelobe confusion increases this to about 
beam
. Figure 5 (click here) shows the distribution of
the local noise-level within the mini-survey. We estimate the noise
level to be determined with an accuracy better than 0.2 mJy beam
.
The noise level is on average 3.9 mJy beam
, and varies between
2.7 and 6.7 mJy beam
. Over 95% (99%) of the area the
noise level is smaller than 4.9 (5.5) mJy beam
. The variation is
therefore more than an order of magnitude larger than the error in the
estimate of the noise, and is caused by systematic effects. To
illustrate this, the map in Fig. 6 (click here) shows the spatial
structure of the variation. Note that the variation in the noise level
shows a correlation length of many degrees, and that the noise level
varies smoothly between frames. From the location of the brightest 4C
sources in this region, it can be clearly seen that some regions of
enhanced local noise are associated with strong radio sources. This is
due to sidelobe confusion.
Figure 6 (click here) also indicates a variation in noise level as a function of declination. Going from low to intermediate declination the noise-level decreases as the effective spacing between individual fields, positioned at points of constant right ascension, decreases. At higher declination the spacing in right ascension between field is raised to increase the efficiency of the mosaicing observations (see Fig. 3 (click here)). This leads to an increase in the noise level at higher declinations.
Finally, interference leads to a non-uniform quality of the data for different fields, resulting in noise variations over the survey area.
Figure 5: The distribution (top) and cumulative distribution (
bottom) of rms-noise levels in the mini-survey
A source list for each frame was compiled using the source-extraction software described previously. The resultant lists were then combined into a final source list. In the case of multiple entries from a source appearing in more than one frame, only the entry with the best signal-to-noise ratio was included. Table 5 (click here) shows a sample of the source list. The complete catalogue of 11299 sources included in the twenty-four frames of the mini-survey can be found in Table 6. For the 477 multiple component sources, the 994 components are also included. This table is only available in electronic form as an ASKII-table at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/Abstract.html. For each source we list:
".
) and integrated (SI, mJy)
flux-densities are listed.
, 
, and the position angle
. 
and 
are in arcseconds,
is measured in degrees from north through east.
Values are only listed for resolved sources/components (see below).
.
Single-component sources are divided into categories of resolved and
unresolved sources. The ratio of integrated to peak flux SI/S was
used to distinguish between these categories. From Monte-Carlo
simulations we found the flux ratio as a function of signal-to-noise
ratio below which 95% of the unresolved sources are located. We
consider all sources with a flux ratio exceeding this 95% limit to be
possibly resolved. A numerical expression for this ratio is given below
(Eq. 10 (click here)).
Note that the values for , and
have not been deconvolved to correct for the beam.
The total number of sources in each category is listed in Table 7 (click here). This table also shows the number of sources in each category for which the source finding algorithm failed to find a good fit. The percentage is especially high (9%) for resolved single component sources. If the source finding algorithm failed to find a good fit for an ``M" source, then it was not able to establish parameters of individual components, other than the position and peak flux density of the local maximum.
Figure 6: Variation of the noise level over the area of the mini-survey.
Contour levels are at noise-levels of 3, 3.5, 4, 4.5, 5 and 6 mJy beam
.
Crosses mark the position of 4C sources with 
To assess the reliability of the source parameters obtained in the analysis of the maps, we used Monte-Carlo simulations. In these simulations Gaussian intensity distributions were added to empty regions in several frames. The major- and minor axes of these distributions were those of the restoring beam. The maximum intensity was varied during the simulation. These sources were then analyzed using the standard source finding algorithm. In this way the distributions of the various parameters as a function of signal-to-noise ratio was established. These distributions were used to investigate biases in the parameters and estimate the errors for the parameters.
From the Monte-Carlo simulations, it was found that the estimates of the flux densities are systematically affected by sampling and noise.
In general, the position on the sky of the pixel with the maximum
detected brightness does not coincide with the actual location of
the maximum of the source. The pixel with maximum detected brightness
in an island measures, in the absence of noise, the flux density at the
pixel nearest to the peak. On average we find that the pixel
with the maximum detected brightness underestimates the peak flux
density by 6%. We therefore adopt the following overall correction to
the peak flux density (
) as measured from moment analysis,
Since the edge of an island is defined by the 2.5
contour, the
area over which the integrated flux density is measured is a function of
the signal-to-noise ratio. This effect will lead to an underestimate of
the integrated flux densities measured from moment analysis.
| Category | with flag `` " | |||
| S sources (unresolved) | 8961 | (79.3%) | 110 | (1.0%) |
| S sources (resolved) | 1858 | (16.4%) | 163 | (1.4%) |
| M sources (2 comp's) | 443 | (4.0%) | 11 | (0.1%) |
| M sources (3 comp's) | 28 | (0.2%) | 0 | |
| M sources (4 comp's) | 6 | (<0.1%) | 0 | |
| E sources | a | 3 | (<0.1%) | |
| C sources (unresolved) | 713 | 22 | ||
| C sources (resolved) | 259 | - | ||
Another bias is introduced by incorporating positive noise peaks (including undetected weak sources) within an island, adding to the integrated flux density, while excluding negative noise peaks from the island, especially when they occur at the fringes of the island. This effect will partly reduce the underestimate of the integrated flux densities measured from moment analysis. We find that for the fit-routine this results in a higher estimate of the peak flux, a higher estimate of the integrated flux, and a lower estimate of the source extension.
All biases discussed here are small (<5%), and only occur at small
signal-to-noise ratios (
), with biases only of the order of 
at a signal-to-noise ratio of 8. Note that the random errors in the flux
density measurements in this regime range from approximately 15% to
25% (see below). Nevertheless, we introduce empirical corrections to the
integrated (
) flux density from moment analysis, and the peak
(
) and integrated (
) flux densities from fitting. These
corrections are only applied to sources for which the signal-to-noise
ratio of the peak pixel 
. The correction factors are
smooth functions of the logarithm of the signal-to-noise ratio, ranging
from 1 at log(
)=1 to approximately 1.06 at
log(
)=0.7
The estimates of the major and minor axis (
) are adjusted to
conserve
the relation 
,
with 
the major and minor
axes of the beam. Thus:
Note that although we search for sources down to a level of 
,
in our source lists we only include sources for which the corrected peak
flux 
. This cut avoids corrections for systematic
effects at very low signal-to-noise ratios that could be as high as 20%,
but are very difficult to establish exactly.
In this section we discuss the errors in the estimates for the position, the peak and integrated flux densities, and the major and minor axes for each source.
It is important to note that the angle over which the rms noise is correlated is comparable to the beamsize. Analytical derivations of the errors in the estimates for the source parameters, based on the assumption of uncorrelated noise, are therefore not valid (See for example: Condon 1996). Empirical expressions, obtained from the Monte-Carlo simulations discussed previously, are therefore used to provide an estimate of the errors for the various parameters. These errors incorporate the random errors introduced by the rms noise as well as the systematic errors introduced by the fit procedures.
We find that all errors can be approximated by a quadratic sum of a
systematic part and a signal-to-noise ratio dependent part, i.e:
The position and flux density measurements are compared with independent data to assess the quality of the data and to search for any systematic errors not included in the Monte-Carlo analysis.
Positional errors can be computed from:
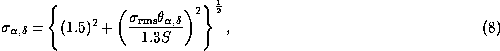
where 
is the local rms-noise, S the peak flux, and
is the source size.
For strong
sources this amounts to a position error of 1.5 arcsec in both
right ascension and declination. The factor 1.3 in the above equation
differs from the usual factor of 2 (Kaper et al. 1966). This is due to
the correlation length of the noise. The factor was established using
the Monte-Carlo simulations.
We have checked the positional accuracy, using two different samples.
Figure 7: a) Normalized position difference for candidate optical IDs of
flat spectrum radio sources (diamonds) and for VLA positions
(crosses). The concentric circles mark the 1, 2, and 3
position differences respectively. b-c) The distribution of
normalized position
differences in right ascension and declination. Overlayed are
the expected Gaussian distributions
A bright sample of sources was selected from the mini-survey, under the
assumption that flat-spectrum sources are predominantly quasars of which
a substantial fraction shows an optical counterpart on the Palomar
Optical Sky Survey plates. This sample comprises 77 sources with S >
150 mJy, a spectral index 
(
,
from Gregory et al. 1996), and an optical candidate
identification (ID) within 10''. These IDs were obtained from the
Cambridge APM catalogue (Irwin et al. 1994). Figure
7 (click here)a shows, as diamonds, the position of candidate IDs
with respect to the radio position, normalized by the estimate of the
errors in 
and 
. The errors were computed by adding the
errors from Eq. (8 (click here)) in quadrature to a positional error of 1''
for the optical ID.
A faint sample was obtained from preliminary results of the CLASS
gravitational lens survey (Myers et al. 1995). As part of this survey a large number of
faint (S<200 mJy), flat-spectrum (
) WENSS sources was
mapped using the VLA at 8.5 GHz in A-array, to search for a characteristic
gravitational lens morphology. Accurate (
) positions for these
sources were obtained as a by-product. Figure 7 (click here)a
shows, as crosses, the VLA positions, with respect to the WENSS
positions, normalized by the errors in right ascension and declination.
Figures 7 (click here)b, c show the combined distribution of position differences of both samples. These figures indicate that the error estimates are probably conservative in the sense that they overestimate the variance in the position difference. However, this overestimate allows for some possible systematic offsets at the 0.5'' level, as indicated by the skew distribution in right ascension.
The relative errors in the flux densities, can be computed from:
with 
the signal-to-noise ratio.
The values for the constants depend on the parameter being measured, and
can be read from the following Table 8 (click here).
| Flux density (method) | (S) |  |  |
| Peak (moment) | ( ) | 0.06 | 1.0 |
| Integr. (moment) | ( ) | 0.04 | 1.7 |
| Peak (fit) | ( ) | 0.04 | 1.3 |
| Integr. (fit) | ( ) | 0.04 | 1.3 |
The constant 
was estimated from Monte-Carlo simulations for
unresolved sources. A conservative estimate for 
includes a 3%
upper limit to the accuracy of the reduction process and source-finding
algorithm and a 
variation in the flux calibration for different
mosaics. For the peak flux we add 5% to the error for the estimate made
through moment analysis to take into account the additional uncertainty
due to sampling.
These errors do not include systematic errors introduced in the data
recording and data reduction. An estimate of these errors can be
obtained by a comparison with results from a standard observation at
92 cm with the WSRT. For this we used a deep (
h) observation
carried out by one of us (G de Bruyn) of a field that is not part of the
mini-survey and compared this with WENSS data already available for this
field. Figure 8 (click here) shows the ratio of integrated flux
densities as measured by WENSS and the standard WSRT observation. This
figure indicates that there are no systematic errors. The figure also
shows that the error estimates are reasonable.
Figure 8: The ratio of integrated flux densities as measured by WENSS
(SIwenss) and a standard WSRT observation (SIdeBruyn),
as a function of the signal-to-noise ratio in WENSS. The curves
represent 
errors, under the assumption that the error in
the standard WENSS observation is comparable to the error in the WENSS data
An estimate of the extendedness of a source can be obtained from the
ratio of the integrated flux to the peak flux 
.
However, a direct application of Eq. (9 (click here)) to establish the
significance of a result SI/S > 1 is only possible if the errors
and 
are independent. This is not the case.
Rather, SI/S shows a very skew distribution, with a tail toward high
flux ratios, especially at low signal-to-noise ratios. The median of
this distribution is found to be less than 1.
To establish a criterion for extendedness, we have determined the upper envelopes of the distribution of SI/S, containing respectively 80%, 90%, 95%, and 99% of the unresolved sources, using Monte-Carlo simulations.
These upper envelopes can be characterized by the equation:
The values for C can be found in Table 9 (click here). Thus substituting
the value 2.4 for C in this equation gives the ratio 
below which lies 95% of the unresolved sources with given 
.
| C | ||
| Envelope | moments | fits |
| 80% | 1.0 | 1.4 |
| 90% | 1.7 | 2.2 |
| 95% | 2.4 | 3.2 |
| 99% | 4.0 | 6.0 |
Figure 9 (click here) shows the distribution the ratio of integrated to peak flux as a function of signal-to-noise ratio. In Fig. 9 (click here)a the lines show the 90% and 95% upper envelopes, used in distinguishing between resolved and unresolved sources. Figures 9 (click here)b and c show the skew distribution of the flux ratio at two different signal-to-noise ratios. This skewness is a property of the distribution for unresolved sources. However, part of the tail can be ascribed to truly resolved sources.
Figure 9: a) The measured ratio of integrated to peak flux as a
function of signal-to-noise ratio for data from the mini-survey.
The lines show the upper envelope containing respectively 90% and 95%
of the unresolved sources, established using Monte-Carlo simulations.
b-c) Two distributions
of the flux ratio at different signal-to-noise ratios. The vertical
lines mark the flux ratio below which one would find 95% of the
unresolved sources. a) 
, b) 
The relative errors in the estimates of the flux densities, the major
and minor axes (
) and the position angle are not independent.
We find, from the Monte-Carlo simulations of unresolved
sources, that at low signal-to-noise ratios (<10) the ellipticity of
sources is overestimated, resulting in an overestimate of the major
axis and an underestimate of the minor axis. Figure 10 (click here)
shows the median values and the errors found for the major and minor
axes as a function of signal-to-noise ratio. The relative error, with
respect to the median, can be expressed with the following relation.
with C=2.5 for the major axis, and C=0.8 for the minor axis.
The lines in Fig. 10 (click here) are given by this expression.
Although Eq. (11 (click here)) has been established from the response of the source finding algorithm to unresolved sources, this expression should give a reasonable approximation of the errors for resolved sources.
The detection of a source with a given intrinsic (noise-free) peak flux
density depends on the ratio of the noise-adjusted peak-flux density
over the local noise level. A source with an intrinsic peak flux density
of 7
will have a noise-adjusted peak density between 5 and
9
in 95% of the cases (assuming a normal distribution for the
noise). From these numbers and from the noise distribution, as
shown in Fig. 5 (click here), we estimate WENSS to be
essentially complete at 30 mJy.
The Euclidean normalized differential source counts for the
mini-survey are shown in Fig. 11 (click here). A comparison with a third
degree polynomial parameterization of the source counts for deep WSRT
92 cm surveys from Wieringa (1991b), shows that WENSS indeed starts to miss
sources below approximately 30 mJy. The detection rate drops below 50%
already at 25 mJy, although the limiting flux density of the survey is
approximately 18 mJy, given a 5
source in a region where the
noise level is 3.5 mJy (less than 20% of the survey area).
Figure 10: The median and standard deviation of the major (top) and minor
axes (bottom) for unresolved sources as a function of signal-to-noise ratio.
The lines represent the error estimate from Eq. (11 (click here)) with
respect to the median. The major and minor axis have been normalized to
the beam size
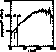
Figure 11: Euclidean normalized differential source counts for the
mini-survey
Appendix A shows contour plots of 120 sources in the mini-survey that have a marked extended structure, and a signal-to-noise ratio of the peak of at least 20. These sources are either resolved single components (``S") sources with a flux-ratio SI/S>1.5, or multiple component (``M") sources with one or more resolved components with SI/S>1.3.
The contour plots are labeled by the source name, type and flag.
Contour levels are 
, 
, 
, 
,
, 
, 
, 
, 
, 
,
, 
, and 
, where 
is the local
noise level, which can be read from the catalogue.
and 
in Eq.
(